11) Определение ускорений точек плоской фигуры

Покажем, что ускорение любой точки М плоской фигуры (так же, как и скорость) складывается из ускорений, которые точка получает при поступательном и вращательном движениях этой фигуры. Положение точки М по отношению к осям Оxy (см.рис.30) определяется радиусом-вектором где . Тогда .

В правой части этого равенства первое слагаемое есть ускорение полюса А, а второе слагаемое определяет ускорение , которое точка м получает при вращении фигуры вокруг полюса A. следовательно, .

Значение , как ускорения точки вращающегося твердого тела, определяется как

где и - угловая скорость и угловое ускорение фигуры, а - угол между вектором и отрезком МА (рис.41).

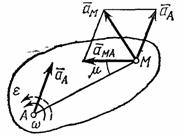
Таким образом, ускорение любой точки М плоской фигуры геометрически складывается из ускорения какой-нибудь другой точки А, принятой за полюс, и ускорения, которое точка М получает при вращении фигуры вокруг этого полюса. Модуль и направление ускорения , находятся построением соответствующего параллелограмма (рис.23).

Однако вычисление с помощью параллелограмма, изображен­ного на рис.23, усложняет расчет, так как предварительно надо бу­дет находить значение угла , а затем - угла между векторами и , Поэтому при решении задач удобнее вектор заменять его касательной и нормальной составляющими и пред­ставить в виде

.

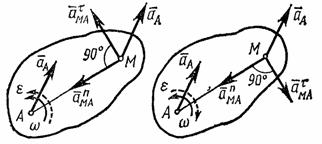
При этом вектор направлен перпендикулярно АМ в сторону вращения, если оно ускоренное, и против вращения, если оно замедленное; вектор всегда направлен от точки М к полюсу А (рис.42). Численно же

.

Если полюс А движется не прямолинейно, то его ускорение мо­жно тоже представить как сумму касательной и нормальной составляющих, тогда

.

 

 

Наконец, когда точка М движется криволинейно и ее траекто­рия известна, то можно заменить суммой .

12) Сложное движение точки

Законы Ньютона сформулированы для движения точки по отношению к инерциальным системам отсчета. Для определения кинематических параметров точки при движении относительно произвольно движущейся системы отсчета вводится теория сложного движения.

Сложным называют движение точки по отношению к двум или нескольким системам отсчета. 

     На рисунке 3.1 показаны:

     - условно принимаемая за неподвижную система отсчета  O1x1y1z1;

     - движущаяся относительно неподвижной система отсчета  Oxyz;

     - точка M, перемещающаяся по отношению к подвижной системе отсчета.

Движение точки  M в данном случае является сложным. Её движение по отношению к подвижной системе отсчета называют относительным движением. 

Движение той точки подвижной системы отсчета, в которой в данный момент находится движущаяся точка, по отношению к неподвижной системе отсчета называют переносным движением. Движение точки M  по отношению к неподвижной системе отсчета называют абсолютным движением. 

По аналогии с этими определениями будут называться относительные, переносные и абсолютные скорости и ускорения точки. Для их обозначения в относительном движении часто всего используется индекс r  (relative – относительный) -Vr, ar  ;  в переносном движении индекс  e  (entrained - увлекать за собой) -Ve , ae . 

   

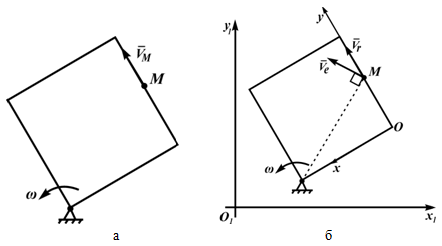
     Ниже приведен пример сложного движения точки -M. 

 На рисунке 3.2,а показан квадрат, вращающийся в плоскости чертежа вокруг неподвижной точки. По стороне квадрата движется точка  M. Она участвует в двух движениях, поэтому можно ввести две системы отсчета: неподвижную, например, O1x1y1z1  - по отношению к которой вращается квадрат и подвижную Oxyz , скрепленную с квадратом, по оси  Oy которой движется точка M  (рисунок  3.2,б). 

Движение точки  M по стороне квадрата (по оси  Oy  скрепленной с квадратом подвижной системы) является относительным - скорость в этом движении Vr . Вращение точки  M  вместе с квадратом - переносное движение, скорость в этом движении - Ve . Абсолютное движение является результатом сложения переносного и относительного движений.