Кинематика

1) Способы задания закона движения точки. Чтобы иметь возможность определить параметры движения точки необходимо задать закон ее движения. В зависимости от известных величин и поставленной задачи могут быть использованы следующие способы задания движения точки.

Векторный способ задания движения точки

     В этом случае положение точки на плоскости или в пространстве определяется вектором-функцией r=r(t)           

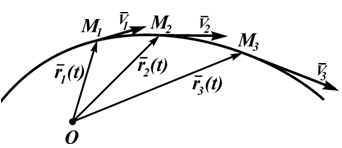
Этот вектор откладывается от неподвижной точки, выбранной за начало отсчета, его конец определяет положение движущейся точки. Годограф r, т.е. положение концов этого вектора в пространстве, определяет траекторию движущейся точки. Ее скорость в этом случае определяется как производная от радиуса-вектора и направлена по касательной к годографу r (по касательной к траектории движения точки, рисунок 1.1):

V=dr/dt           

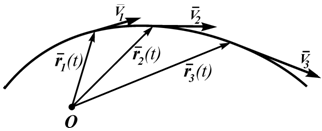
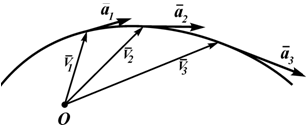
 Ускорение точки (изменение ее скорости) определяется как производная от скорости:

Вектор ускорения направлен по касательной к годографу вектора скорости.

Определение скорости и ускорения точки при естественном способе задания движения.

Из определения скорости точки где

- единичный вектор касательной, тогда

Алгебраическая скорость – это проекция вектора скорости на касательную, равная производной от дуговой координаты по времени. Если производная положительна, то точка движется в положительном направлении отсчета дуговой координаты.

Из определения ускорения

поскольку τ - переменный по направлению вектор, то:

Производная определяется только свойствами траектории в окрестности данной точки, при этом

n - единичный вектор главной нормали,

ρ   - радиус кривизны траектории в данной точке.

Таким образом,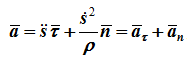

т.е. вектор ускорения раскладывается на две составляющие - касательное и нормальное ускорения: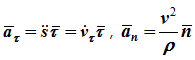 Здесь:

- алгебраическое значение касательного ускорения (проекция вектора ускорения на касательную) характеризует изменение скорости по величине;

– нормальное ускорение (проекция вектора ускорения на главную нормаль) характеризует изменение скорости по направлению. Вектор ускорения всегда лежит в соприкасающейся плоскости и проекция ускорения на бинормаль равна нулю (ab=0).

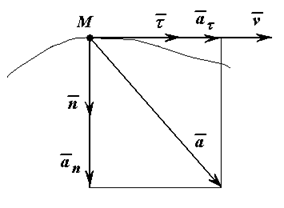Движение точки ускоренное, если знаки проекций векторов скорости и ускорения на касательную совпадают.

2) Координатный способ задания движения точки. В выбранной системе координат задаются координаты движущейся точки как функции от времени. В прямоугольной декартовой системе координат это будут уравнения: x=x(t) y=y(t)           z=z(t)

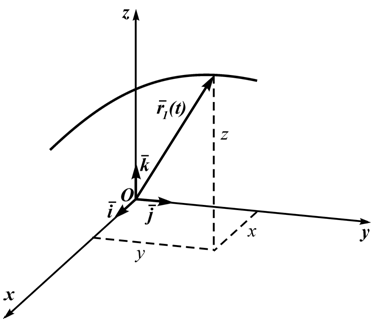
     Эти уравнения являются и уравнениями траектории в параметрической форме. Исключая из этих уравнений параметр t, можно получить три пары систем двух уравнений, каждая из которых представляет траекторию точки, как пересечение поверхностей. Кроме декартовых могут быть использованы другие системы координат (сферическая, цилиндрическая). Всегда можно перейти от координатного способа задания движения к векторному (рисунок 1.3):

  r(t)=i⋅x(t) ⊕ j⋅y(t) ⊕ k⋅z(t) 

   Поэтому, используя формулы для определения скорости и ускорения точки при векторном способе задания движения, можно получить аналогичные формулы для координатного способа:

  То есть:

 

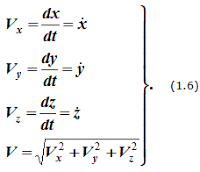 Направление вектора скорости определяется с помощью направляющих косинусов:    

 

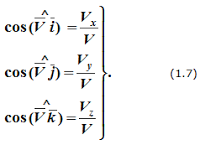
Формулы (1.6) и (1.7) полностью определяют вектор скорости при координатном способе задания движения точки, т.е. по величине и направлению.Аналогичны формулы для определения ускорения точки:

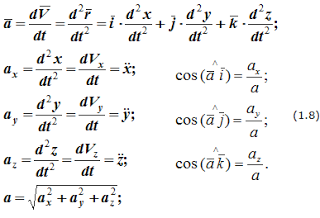 Формулы (1.8) определяют величину и направление вектора ускорения. В формулах (1.6) и (1.8) приведены используемые в различных учебниках обозначения проекций скоростей и ускорений точек на оси декартовой системы координат.

3) Естественный способ задания движения точки.

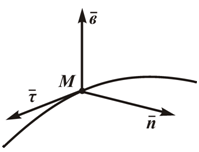
τ-орт касательной;n-орт нормали;b-орт бинормали; При естественном способе задания движения предполагается определение параметров движения точки в подвижной системе отсчета, начало которой совпадает с движущейся точкой, а осями служат касательная, нормаль и бинормаль к траектории движения точки в каждом ее положении. Единичные орты  τ, n ,b определяют направление соответствующих осей в каждой точке кривой.

 Чтобы задать закон движения точки естественным способом необходимо:

1) знать траекторию движения;

2) установить начало отсчета на этой кривой;

3) установить положительное направление движения;

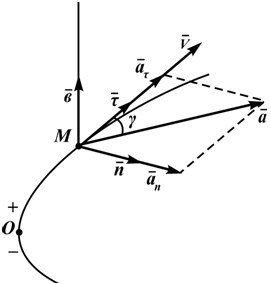
4) дать закон движения точки по этой кривой, т.е. выразить расстояние от начала отсчета до положения точки на кривой в данный момент времени ∪OM=S(t) .Зная эти параметры можно найти все кинематические характеристики точки в любой момент времени (рисунок 1.5).  Скорость точки определяется по формулам (1.9)V=τ⋅dS/dt,    V=dS/dt.   (1.9)

Первая формула определяет величину и направление вектора скорости, вторая формула только величину. Ускорение определяется как производная от вектора скорости:

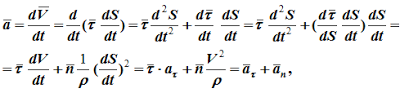
 т.е.  a=a_τ+a_n.   (1.10)В формуле (1.10)

 a_τ=τ⋅dV/dt=τ⋅d²S/dt², a_τ=dV/dt=τ⋅d²S/dt²- касательное ускорение; оно характеризует быстроту изменения величины скорости точки;

a_n=n⋅V²/ρ, a_n=V²/ρ - нормальное ускорение точки; характеризует быстроту изменения направления вектора скорости;

 ρ - радиус кривизны траектории в данной точке (например, для окружности:ρ=R  , для прямой линии ρ=∞ ).Полное ускорение точки определяется следующим образом (рисунок 1.5):

Выше отмечалось,  что всегда можно перейти от одного способа задания закона движения точки к другому. Поэтому, преобразовывая одни и те же формулы, можно получить другое их написание.    Например,  

или   a_τ=acosγ (рисунок 1.5).Далее 

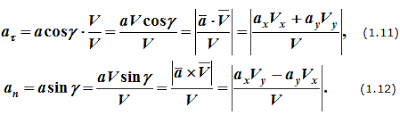
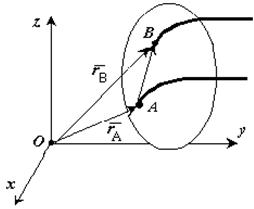
4) Поступательное движение – это движение, при котором любая прямая, связанная с телом, перемещается параллельно самой себе. Теорема. При поступательном движении твердого тела траектории, скорости и ускорения точек тела одинаковы. Доказательство. Если выбрать две точки твердого тела А  и В, то радиусы-векторы этих точек связаны соотношением .Траектория точки А  – это кривая, которая задается функцией r_A(t), а  траектория точки B – это кривая, которая задается функцией r_B(t). Траектория точки B получается переносом траектории точки A в пространстве вдоль вектора AB, который не меняет своей величины и направления во времени (AB = const). Следовательно, траектории всех точек твердого тела одинаковы. Продифференцируем по времени выражение

Получаем

Продифференцируем по времени скорость и получим выражение a_B = a_A.

Следовательно, скорости и ускорения всех точек твердого тела одинаковы.

Для задания поступательного движения твердого тела достаточно задать движение одной из его точек:

5) Вращением твердого тела вокруг неподвижной оси называют движение, при котором хотя бы две точки тела все время остаются неподвижными. Прямая, проходящая через эти точки, называется осью вращения. 

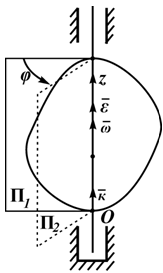Вращательное движение определяется двугранным углом φ  между двумя плоскостями, проходящими через ось вращения. Одна из этих плоскостей неподвижна, вторая скреплена с твердым телом и поворачивается вместе с ним (рисунок 2.3). Изменение этого угла с течением времени и есть закон вращательного движения: φ=φ(t), рад.        (2.2) Положительным считается угол, откладываемый против хода часовой стрелки, если смотреть навстречу выбранному направлению оси вращения (ось  Oz на рисунке 2.3). Угол измеряется в радианах.

Скорость вращения тела, определяющаяся приращением угла поворота тела за промежуток времени называется угловой скоростью.  Быстрота изменения угла φ – это угловая скорость: ω=dφ/dt=φ', рад/с; с-1. (2.3)

Приняв k  как единичный орт положительного направления оси, получим

Вектор угловой скорости – скользящий вектор: он может быть приложен к любой точке оси вращения и всегда направлен вдоль оси, при положительном значении угловой скорости направления ω  и k  совпадают, при отрицательном – противоположны.

Изменение угловой скорости характеризуется угловым ускорением:

Вектор углового ускорения так же направлен по оси вращения. При ускоренном вращении их направления совпадают, при замедленном - противоположны.

Для некоторых частных случаев вращательного движения могут быть использованы формулы:

- равномерное вращение ( ω - const) φ=φ0+ωt;                                 (2.5)

- равнопеременное вращение ( ε - const) ω=ω0+εt; φ=φ0+ω0t+εt2/2.         (2.6)

В технике угловая скорость часто задается в оборотах в минуту n[об/мин]. Один оборот – это 2π  радиан: ω=n⋅2π/60=nπ/30 рад/с; с-1.

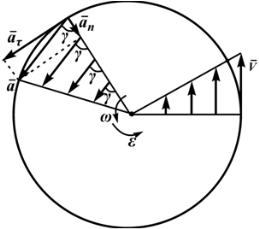
6)  При вращении твердого тела вокруг неподвижной оси каждая точка тела движется по окружности. Радиус окружности R равен расстоянию от точки до оси вращения. Закон движения точки может быть задан естественным способом (рисунок 2.4): траектория – окружность; начало отсчета точка O₁  и положительное направление движения выбраны, длина дуги (дуговая координата) определяется по формуле 

Скорость точки

V=dS/dt=dφ⋅R/dt=ωR          (2.9)

Скорость направлена по касательной к траектории, поэтому можно написать

Вектор скорости можно получить векторным произведением: V=ω⊗ r,  V=ω⋅rsinα=ωR.

Ускорение при естественном способе задания движения определяется как сумма касательного и нормального ускорений (см. вывод формулы (1.10)):

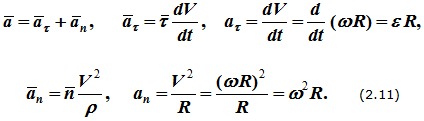
Эти же выражения можно получить, взяв производную от векторного произведения V=ω⊗ r  . Угол, который составляет полное ускорение с радиусом, может быть определен из соотношения (рисунок 2.5) То есть эти углы для всех точек тела одинаковы и не зависят от их расположения на теле. На этом же рисунке представлены законы распределения скоростей и ускорений точек во вращающемся теле в зависимости от расстояния их до оси вращения. Эти законы распределения соответствуют формулам:  

7) Угловая скорость и угловое ускорение. Рассмотрим твердое тело, которое вращается вокруг неподвижной оси. Тогда отдельные точки этого тела будут описывать окружности разных радиусов, центры которых лежат на оси вращения. Пусть некоторая точка движется по окружности радиуса R (рис. 1). Ее положение через промежуток времени Δt зададим углом Δφ. Элементарные (бесконечно малые) повороты можно рассматривать как векторы (они обозначаются Δφ или dφ). Модуль вектора dφ равен углу поворота, а его направление совпадает с направлением поступательного движения острия винта, головка которого вращается в направлении движения точки по окружности, т. е. подчиняется правилу правого винта (рис. 1). Векторы, направления которых связываются с направлением вращения, называются псевдовекторами или аксиальными векторами. Эти векторы не имеют определенных точек приложения: они могут откладываться из любой точки оси вращения. 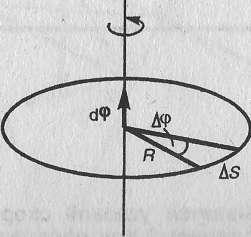Угловой скоростью называется векторная величина, равная первой производной угла поворота тела по времени: Вектор ω направлен вдоль оси вращения по правилу правого винта, т. е. так же, как и вектор dφ (рис. 2). Размерность угловой скорости dim ω = Т^-1, а ее единица — радиан в секунду (рад/с).

v=ωR

В векторном виде формулу для линейной скорости можно написать как векторное произведение: При этом модуль векторного произведения, по определению, равен ωRsin(ω, R), а направление совпадает с направлением поступательного движения правого винта его вращения от ω к R.

Угловым ускорением называется векторная величина, равная первой производной yгловой скорости по времени:

Тангенциальная составляющая ускорения aτ=dv/dt , v = ωR и Нормальная составляющая ускорения Значит, связь между линейными (длина пути s, пройденного точкой по дуге окружности радиуса R, линейная скорость v, тангенциальное ускорение аτ, нормальное ускорение аn) и угловыми величинами (угол поворота φ, угловая скорость ω, угловое ускорение ε) выражается следующими формулами:

s = Rφ, v = Rω, аτ = R?, an = ω2R.

В случае равнопеременного движения точки по окружности (ω=const)

ω = ω0 ± ?t, φ = ω0t ± ?t2/2,

где ω0 — начальная угловая скорость.