Условия равновесия произвольной плоской системы сил. Случай параллельных сил.

Для равновесия любой плоской системы сил необходимо и достаточно, чтобы одновременно выполнялись условия: R = 0, M₀ = 0.Здесь О - любая точка плоскости.Найдем вытекающие из равенств аналитические условия равновесия. Величины R и М_о определяются равенствами:

где Но R может равняться нулю только тогда, когда одновременно R_x = 0 и R_y = 0. Следовательно, условия будут выполнены, если будет:

Равенства выражают, следующие аналитические условия рав­новесия: для равновесия произвольной плоской системы сил, необходимо и достаточно, чтобы суммы проекций всех сил на каж­дую из двух координатных осей и сумма их моментов относительно любого центра, лежащего в плоскости действия сил, были равны нулю.

Теорема о трех моментах. Для равновесия плоской системы сил, действующих на твердое тело, необходимо и достаточно, чтобы суммы моментов этих сил системы относительно трех любых точек, расположенных в плоскости действия сил и не лежащих на одной прямой, были равны нулю.

; ;

10) Равновесие произвольной плоской системы сил

При равновесии произвольной плоской системы сил уравнения равновесия могут быть записаны в виде ∑xi=0;  ∑yi=0; ∑Mo=0,причем оси и точка O , относительно которой пишется уравнение моментов, выбираются произвольно.     Уравнения равновесия также могут быть записаны иначе:

 ∑xi =0; ∑MA=0;  ∑MB=0.  Здесь ось Ox  не должна быть перпендикулярна линии, проходящей через точки A  и B . ∑MA=0; ∑MB=0; ∑MC=0.В задачах такого типа число неизвестных плоской системы сил не должно превышать трех, иначе система станет статически неопределимой.

11) Рассмотрим систему параллельных сил  {F1, F2, ..., Fn}. При повороте всех сил системы на один и тот же угол линия действия равнодействующей системы параллельных сил повернется в ту же сторону на тот же угол вокруг некоторой точки (рисунок 1.5, а).Эта точка называется центром параллельных сил. Согласно теореме Вариньона, если система сил имеет равнодействующую, то ее момент относительно любого центра (оси) равен сумме моментов всех сил системы относительно того же центра (оси).

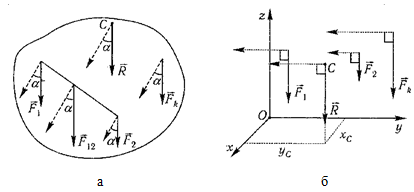
Для определения координат центра параллельных сил воспользуемся этой теоремой.

Относительно оси x 

 Mx(R) = ΣMx(Fk),    - yCR = ΣykFk        и        yC = ΣykFk /ΣFk.

Относительно оси y 

 My(R) = ΣMy(Fk),       - xCR = ΣxkFk        и       xC = ΣxkFk /ΣFk.

Чтобы определить координату  zC, повернем все силы на 90° так, чтобы они стали параллельны оси  y (рисунок 1.5, б). Тогда Mz(R) = ΣMz(Fk),        - zCR = ΣzkFk        и       zC = ΣzkFk /ΣFk.

Следовательно, формула для определения радиус-вектора центра параллельных сил принимает вид  rC = ΣrkFk /ΣFk.

Свойства центра параллельных сил:

1 Сумма моментов всех сил  Fk  относительно точки  C  равна нулю   ΣMC(Fk) = 0.

2 Если все силы повернуть на некоторый угол  α, не меняя точек приложения сил, то центр новой системы параллельных сил будет той же точкой  C.

12) Центром тяжести твердого тела называется геометрическая точка, жестко связанная с этим телом, и являющаяся центром параллельных сил тяжести, приложенных к отдельным элементарным частицам тела (рисунок 1.6).Радиус-вектор этой точки

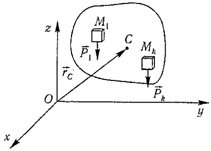
Для однородного тела положение центра тяжести тела не зависит от материала, а определяется геометрической формой тела.Если удельный вес однородного тела  γ, вес элементарной частицы тела P_{k =} γΔV_k  (P ₌ γV) подставить в формулу для определения  r_C, имеем

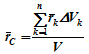Откуда, проецируя на оси и переходя к пределу, получаем координаты центра тяжести однородного объема

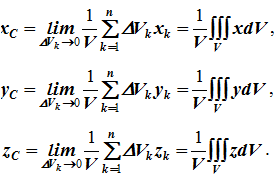
Аналогично для координат центра тяжести однородной поверхности площадью S  (рисунок 1.7, а)

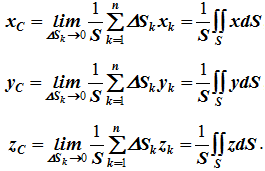
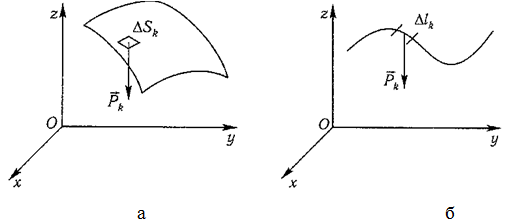
Для координат центра тяжести однородной линии длиной L  (рисунок 1.7, б)

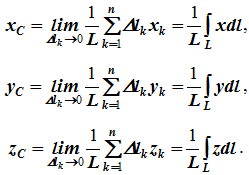
13) Исходя из полученных ранее общих формул, можно указать способы определения координат центров тяжести твердых тел:

1 Аналитический (путем интегрирования).

2 Метод симметрии. Если тело имеет плоскость, ось или центр симметрии, то его центр тяжести лежит соответственно в плоскости симметрии, оси симметрии или в центре симметрии.

3 Экспериментальный (метод подвешивания тела).

4 Разбиение. Тело разбивается на конечное число частей, для каждой из которых положение центра тяжести C  и площадь  S известны. Например, проекцию тела на плоскость xOy  можно представить в виде двух плоских фигур с площадями S₁  и  S₂ (S = S₁ + S₂). Центры тяжести этих фигур находятся в точках  C₁(x₁, y₁) и  C₂(x₂, y₂). Тогда координаты центра тяжести тела равны

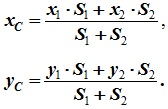
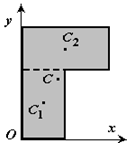
5 Дополнение (метод отрицательных площадей или объемов). Частный случай способа разбиения. Он применяется к телам, имеющим вырезы, если центры тяжести тела без выреза и вырезанной части известны. Например, необходимо найти координаты центра тяжести плоской фигуры (рисунок 1.9):

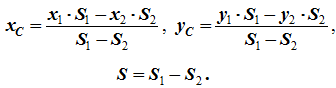
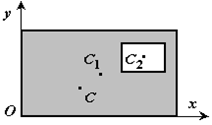
1 Треугольник

Центр тяжести площади треугольник совпадает с точкой пересечения его медиан (рисунок 1.10, а).

 DM = MB,  CM = (1/3)AM.

2 Дуга окружности

Дуга имеет ось симметрии (рисунок 1.10, б). Центр тяжести лежит на этой оси, т.е.  y_C = 0.

dl  – элемент дуги,  dl = Rdφ,  R – радиус окружности,  x = Rcosφ,  L = 2αR,

Следовательно:

 x_C = R(sinα/α).

3 Круговой сектор

Сектор радиуса  R с центральным углом  2α имеет ось симметрии  Ox, на которой находится центр тяжести (рисунок 1.10, в). 

Разбиваем сектор на элементарные секторы, которые можно считать треугольниками. Центры тяжести элементарных секторов располагаются на дуге окружности радиуса  (2/3)R. 

Центр тяжести сектора совпадает с центром тяжести дуги  AB:

14)  При стремлении сдвинуть тело, лежащее на шероховатой поверхности, возникает сила реакции R, которая имеет две составляющие – нормальную N и силу трения  F_mp.  В теоретической механике обычно рассматривается только сухое трение между поверхностями, при этом различают трение при покое или равновесии тела и трение скольжения при движении одного тела по поверхности другого с некоторой относительной скоростью.

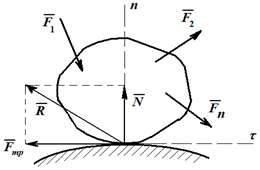 При покое сила трения зависит только от активных сил и может быть определена):

 F_mp=∑F_iτ. В результате экспериментальных исследований французскими учеными Гийомом Амонтоном и Шарлем Кулоном были установлены законы для сухого трения:   1) сила трения находится в общей касательной плоскости соприкасающихся поверхностей тел и направлена в сторону, противоположную направлению возможного скольжения тела под действием активных сил. Величина силы трения зависит от активных сил и заключена между нулем и своим максимальным значением, которое достигается в момент выхода тела из положения равновесия:

0≤F_mp≤F_mp^max; 2) максимальное значение силы трения при прочих равных условиях не зависит от площади контакта трущихся поверхностей и пропорционально нормальной реакции:

  F_mp^max=fN  [Н],

где f – коэффициент трения, являющийся безразмерной величиной и зависящий от материала и физического состояния трущихся поверхностей.

Если твердое тело под действием активных сил находится на шероховатой поверхности в предельном состоянии равновесия (сила трения достигает своего максимального значения), то полная реакция шероховатой поверхности   отклонена от нормали к общей касательной плоскости трущихся поверхностей на наибольший угол φ, который называют углом трения (рисунок 2.17). При этом

 tgφ=F_mp^max/N=fN/N=f  .  То есть тангенс угла трения равен коэффициенту трения.

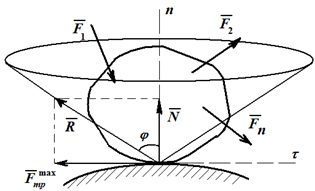
    Конусом трения называют конус, описанный линией действия полной реакции, построенной на максимальной силе трения, вокруг направления нормальной реакции.

Для равновесия тела на шероховатой поверхности необходимо и достаточно, чтобы линия действия равнодействующей активных сил, действующих на тело, проходила внутри конуса трения или по его образующей через его вершину.

15) Равновесие при наличии трения скольжения

При скольжении тела по шероховатой поверхности возникает сила реакции, которая имеет две составляющие – нормальную и силу трения скольжения (рисунок 2.1). Сила трения скольжения, приложенная к одному из трущихся тел, направлена противоположно его скорости относительно второго тела.

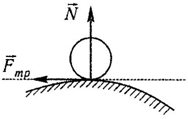
В результате экспериментальных исследований были установлены законы Амонтона-Кулона:

1) сила трения скольжения находится в общей касательной плоскости соприкасающихся поверхностей тел и направлена в сторону, противоположную направлению возможного скольжения тела под действием активных сил. Величина силы трения зависит от активных сил и заключена между нулем и своим максимальным значением, которое достигается в момент выхода тела из положения равновесия (0 ≤ F_тр ≤ F_тр^max );

2) максимальное значение силы трения скольжения не зависит от площади контакта, а определяется величиной нормальной реакции, материалом и состоянием контактирующих поверхностей;

F_тр^max = fN,где  f – коэффициент трения скольжения, который является безразмерной величиной и зависит от материала и физического состояния трущихся поверхностей, а также от скорости движения тела и удельного давления.Экспериментально установлено, что  f < f_сц.

Рассмотрим твердое тело на шероховатой поверхности (рисунок 2.2), находящееся под действием активных сил в предельном состоянии равновесия, т.е. когда сила трения достигает своего наибольшего значения при данном значении нормальной реакции.В этом случае полная реакция шероховатой поверхности отклонена от нормали к общей касательной плоскости трущихся поверхностей на наибольший угол (R^max ). Этот наибольший угол между полной реакцией, построенной на наибольшей силе трения при данной нормальной реакции и направлением нормальной реакции, называется углом трения  φ:tgφ = F_тр^max/N = fN/N = f.

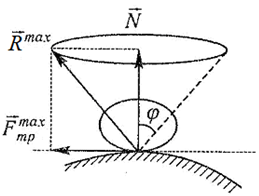
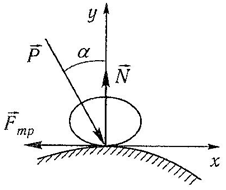
Конус трения – поверхность, образованная линией действия максимальной реакции опорной поверхности при движении тела в различных направлениях).При равновесии тела на шероховатой поверхности под действием силы P можно составить два уравнения равновесия:

 ΣF_{kx = 0};  Psinα - F_{тр = 0}; ΣF_{ky = 0};  - Pcosα + N = 0.Следовательно,

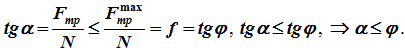
Для равновесия тела на шероховатой поверхности необходимо и достаточно, чтобы линия действия равнодействующей активных сил, действующих на тело, проходила внутри конуса трения или по его образующей через его вершину. Никакая сила, лежащая внутри конуса трения, не может вывести тело из состояния равновесия.

16) Трением качения называется сопротивление, возникающее при качении одного тела по поверхности другого. Вследствие деформации тел их касание происходит вдоль площадки AB, появляется распределенная система сил реакций, которая, согласно основной теореме статики, может быть заменена силой и парой (рисунок 2.18). Сила раскладывается на две составляющие – нормальную N и силу трения F_mp; пара сил называется моментом сопротивления качению M_C.

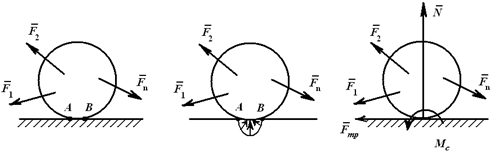
    При равновесии тела момент сопротивления качению определяется из условий равновесия системы сил. При этом установлено, что момент сопротивления принимает значения от нуля до максимального значения. Максимальное значение момента сопротивления, соответствующее началу качения, определяется равенством M_{C max}=δN  [Нм], где δ – коэффициент трения качения, измеряемый в метрах и зависящий от материала контактирующих тел и геометрии зоны контакта.

17) Фермой называется жесткая конструкция из прямолинейных стержней, соединенных на концах шарнирами. Если все стержни фермы лежат в одной плоскости, ферма называется плоской. Места соединения стержней фермы называют узлами. Все внешние нагрузки к ферме прикладываются только в узлах. При расчете фермы трением в узлах и весом стержней (по сравнению с внешними нагрузками) пренебрегают или распределяют веса стержней по узлам. Тогда на каждый из стержней фермы будут действовать две силы, приложен­ные к его концам, которые при равновесии могут быть направлены только вдоль стержня. Следовательно, можно считать, что стержни фермы работают только на растяжение или на сжатие. Огра­ничимся рассмотрением жестких плоских ферм, без лишних стержней, образованных из треугольников. В таких фермах число стержней и число узлов связаны соотношением

Расчет фермы сводится к определению опорных реакций и уси­лий в ее стержнях.

Опорные реакции можно найти обычными методами статики, рассматривая ферму в целом как твердое тело. Перейдем к определе­нию усилий в стержнях.

Метод вырезания узлов. Этим методом удобно пользоваться, когда надо найти усилия во всех стержнях фермы. Он сводится к по­следовательному рассмотрению условий равновесия сил, сходящихся в каждом из узлов фермы. Ход расчетов поясним на конкретном примере.

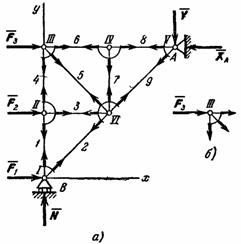
Рассмотрим изображенную на рис. 23,а ферму, образованную из одинаковых равнобедренных прямоугольных треугольников; действую­щие на ферму силы парал­лельны оси х и равны: F₁ = F₂ = F₃ = F = 2.В этой ферме число узлов n = 6, а число стержней k = 9. Следовательно, соот­ношение выполняется и ферма является жесткой, без лишних стержней.

Составляя уравнения рав­новесия для фермы в целом, найдем, что реакции опор направлены, как пока­зано на рисунке, и численно равны;

Переходим к определению усилий в стержнях.Пронумеруем узлы фермы римскими цифрами, а стержни — арабскими. Искомые усилия будем обозначать S₁ (в стержне 1), S₂ (в стержне 2) и т. д. Отрежем мысленно все узлы вместе со сходящимися в них стержнями от осталь­ной фермы. Действие отброшенных частей стержней заменим силами, которые будут направлены вдоль соответствующих стержней и численно равны искомым усилиям S₁, S₂, ... Изображаем сразу все эти силы на рисунке, направляя их от узлов, т. е. считая, все стержни растя­нутыми (рис. 23, а; изображенную картину надо представлять себе для каждого узла так, как это показано на рис. 23, б для узла III). Если в результате расчета величина усилия в каком-нибудь стержне получится отрицательной, это будет означать, что данный стержень не растянут, а сжат. Буквенных обозначений для сил, действующих вдоль стержней, ни рис. 23 не вводам, поскольку ясно, что силы, действующие вдоль стержня 1, равны численно S₁, вдоль стержня 2 — равны S₂ и т. д.

Теперь для сил, сходящихся в каждом узле, составляем последо­вательно уравнения равновесия

Начинаем с узла 1, где сходятся два стержня, так как из двух уравнений равновесия можно определить только два неизвестных усилия.

Составляя уравнения равновесия для узла 1, получим Отсюда находим Теперь, зная S₁, переходим к узлу II. Для него уравнения равнове­сия дают откуда

Определив S₄, составляем аналогичным путем уравнения равновесия сначала для узла III, а затем для узла IV. Из этих уравнений находим:

Наконец, для вычисления S₉ составляем уравнение равновесия сил, сходящихся в узле V, проектируя их на ось By. Получим откуда

Второе уравнение равновесия для узла V и два уравнения для узла VI можно составить как поверочные. Для нахождения усилий в стержнях эти уравнения не понадобились, так как вместо них были использованы три уравнения равновесия всей фермы в целом при определении N, Х_А, и Y_А.Окончательные результаты расчета можно свести в таблицу:

№ стержня ..........	1	2	3	4	5	6	7	8	9
Усилие в Н .........	-1	-2,82	-2	-1	+1,41	-3	0	-3	-4,23

Как показывают знаки усилий, стержень 5 растянут, остальные стер­жни сжаты; стержень 7 не нагружен (нулевой, стержень).

Наличие в ферме нулевых стержней, подобных стержню 7, обна­руживается сразу, так как если в узле, не нагруженном внешними силами, сходятся три стержня, из которых два направлены вдоль одной прямой, то усилие в третьем стержне равно нулю. Этот результат получается из уравнения равновесия в проекции на ось, перпендикулярную к упомянутым двум стержням.

Если в ходе расчета встретится узел, для которого число неизве­стных больше двух, то можно воспользоваться методом сечений.

Метод сечений (метод Риттера). Этим методом удобно поль­зоваться для определения усилий в отдельных стержнях фермы, в ча­стности, для проверочных расчетов. Идея метода состоит в том, что ферму разделяют на две части сечением, проходящим через три стержня, в которых (или в одном из которых) требуется определить усилие, и рассматривают равновесие одной из этих частей. Действие отброшенной части заменяют соответствующими силами, направляя их вдоль разрезанных стержней от узлов, т. е. считая стержни рас­тянутыми (как и в методе вырезания узлов). Затем составляют урав­нения равновесия, беря центры моментов (или ось проекций) так, чтобы в каждое уравнение вошло только одно неизвестное усилие.