Расчет трехшарнирных арок

Трехшарнирной аркой (рамой) называется статически определимая распор-ная система, состоящая их двух полуарок (полурам), соединенных между собой и с поверхностью земли шарнирами.

Арка – распорная система, имеющая форму кривого стержня, обращенная выпуклостью навстречу действию основной нагрузки:

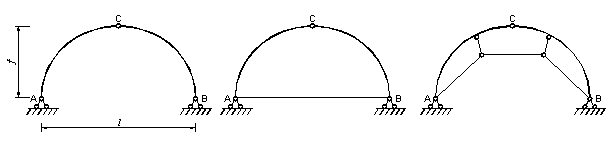
Выделяют следующие элементы арки: левая полуарка АС и правая по-луарка СВ, пятовые (опорные) шарниры в точках А и В, ключевой шарнир в точке С, затяжка – элемент, соединяющий опорные шарниры А и В, подвески – элементы, поддерживающие затяжку. Основными геометрическими парамет-рами арки являются: пролет (или длина пролета) - l и стрела подъема (или вы-сота арки в ключе) - f .

Очертание арки может быть произвольным, рациональным, но чаще всего ось арки задается очерченной по закону квадратной параболы или окружности. При очертании оси арки:

а) по закону квадратной параболы

- уравнение оси имеет вид:

- тангенс угла наклона касательной к оси арки

б) по закону окружности

- уравнение оси имеет вид , где ,

- синус угла наклона касательной к оси арки ,

- косинус угла наклона касательной к оси арки .

Трехшарнирные системы являются распорными, т.е. под действием нагрузки любого типа (вертикальной или горизонтальной) в них возникают горизонтальные составляющие опорных реакций - распор, которые принято обозначать символом «Н».

Аналитический расчет трехшарнирных систем.

Целью аналитического расчета трехшарнирных систем является определе-ние внутренних силовых факторов: поперечной силы, продольной силы, изгибаю-щего момента.

Аналитический расчет начинают с определения опорных реакций. Для опре-деления вертикальных составляющих опорных реакций составляют уравнения равенства нулю сумм моментов всех сил, приложенных к арке, относительно пятовых (опорных) шарниров:

проверка вертикальных составляющих опорных реакций:

Для определения горизонтальных составляющих опорных реакций состав-ляют уравнения равенства нулю сумм моментов всех сил, приложенных к левой полуарке и правой полуарке, относительно ключевого шарнира:

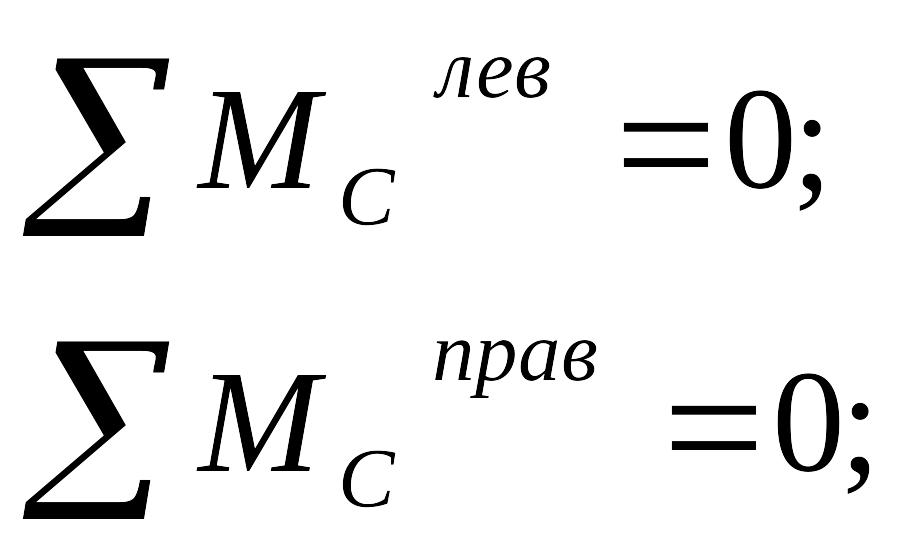
из последних уравнений величину распора Н выразим в виде равенства:

, где - «балочный» изгибающий момент относительно ключевого шарнира С, f - стрела подъема арки.

проверка правильности определения горизонтальных составляющих опорных реакций:

;

Определение внутренних силовых факторов в сечении арки

Поперечная сила в сечении к- Q_К определяется как алгебраическая сумма проекций всех сил, приложенных по одну сторону от сечения на ось, перпендику-лярную касательной, проведенной к оси арки в сечении к (на плоскость сечения):

,

где - балочная поперечная сила в сечении к, - угол наклона касса-тельной, проведенной к оси арки в сечении к.

Поперечная сила считается положительной, если стремится повернуть отсеченный элемент по ходу часовой стрелки.

Изгибающий момент в сечении к - М К- определяется как алгебраическая сумма моментов всех сил, приложенных по одну сторону от сечения -относи-тельно центра сечения:

,

где - балочный изгибающий момент, Н- распор, у_К- ордината сечения к.

Изгибающий момент в сечении М_К считается положительным, если создаю-щая его сила стремится повернуть отсеченный элемент таким образом, что растя-нутыми оказываются нижние волокна элемента.

Продольная (нормальная ) сила в сечении к –N_К -определяется как алгеб-раическая сумма проекций всех сил, приложенных по одну сторону от сечения на касательную, проведенную к оси арки в сечении к (на нормаль к плоскости сече-ния):

,

где - балочная поперечная сила в сечении к , - угол наклона касса-тельной, проведенной к оси арки в сечении к, H - распор.

Продольная сила считается положительной, если стремится растянуть отсе-ченный элемент.

Анализ выражений внутренних усилий в арке позволяет сделать следующие выводы:

Изгибающий момент в арке меньше изгибающего момента в соответст-вующем сечении балки.

Поперечная сила в арке меньше поперечной силы в соответствующем сече-нии балки.

Продольная сила в арке оказывает только сжимающее действие.