5 .5.3. Utrudnienia I pułapki.

Oczywiście nie zawsze badane wyrażenia są tak łatwe do zaznaczenia na diagramie jak w dwóch rozważanych dotąd zadaniach. Poniżej omówimy kilka przykładów nieco bardziej skomplikowanych.

Czy tam ma być plus czy minus?

Przykład:

Sprawdzimy, czy jest prawem rachunku zbiorów wyrażenie:

(B  A    A  C’ = )  B  C  

Pierwszy człon poprzednika implikacji informuje nas, że coś się musi znajdować w części wspólnej (iloczynie) zbiorów B i A. Ponieważ obszar ten składa się z dwóch kawałków, nie wiemy dokładnie, w którym z nich jakiś element się znajduje; być może w obydwu, ale może tylko w jednym z nich. Dlatego też możemy wpisać tu jedynie plusy ze znakiem zapytania.

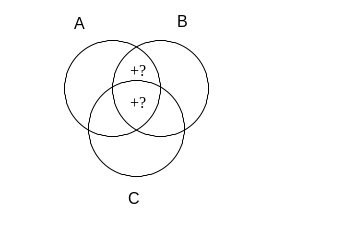
Drugi człon poprzednika implikacji informuje nas, że pusty musi obszar wspólny A oraz C’, czyli ta część zbioru A, która znajduje się poza zbiorem C. Na naszym rysunku są to dwa „górne” kawałki zbioru A. Widzimy, że w jednej z tych części znajduje się znak „+?”. Ponieważ jednak znak zapytania świadczy, że coś w tym obszarze może się znajdować, ale nie jest to konieczne, a teraz otrzymujemy informacje, że na pewno nic tam nie ma, to wynikający stąd minus jest „silniejszy” od plusa ze znakiem zapytania i dlatego właśnie „–” powinien się tam ostatecznie znaleźć. Jeśli jednak jeden ze znaków „+?” zamienimy na minus, to wynika stąd, że drugi z plusów staje się „pewny” i widniejący przy nim pytajnik powinniśmy zlikwidować. Skoro bowiem dotąd wiedzieliśmy, ze w jednym z dwóch obszarów coś jest, lecz nie mieliśmy pewności w którym, a teraz dowiedzieliśmy, że pierwszy jest pusty, to w takim razie na pewno zapełniony musi być obszar drugi. A zatem, po wpisaniu całego poprzednika implikacji, diagram będzie się przedstawiał następująco:

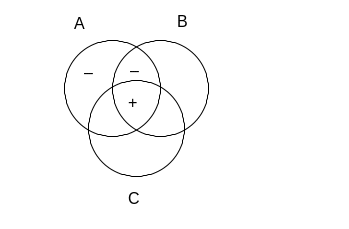
Teraz musimy sprawdzić, czy tak wykonany rysunek daje nam gwarancję prawdziwości następnika implikacji, a więc czy na pewno B  C  . W jednym kawałku części wspólnej zbiorów B i C mamy plus, który daje nam gwarancję, że obszar ten z pewnością nie jest pusty. Badane wyrażenie jest zatem prawem rachunku zbiorów.

▲

Plus ze znakiem zapytania nie daje pewności!

Przykład:

Sprawdzimy, czy jest prawem rachunku zbiorów wyrażenie:

(B  C’  A – C  )  C’  B  

Fakt, że zbiór B zawiera się w dopełnieniu C, oznacza, że cały B znajduje się poza C, czyli żadna część B nie może znajdować się w C; zbiory te są prostu rozłączne. W całej części wspólnej B i C musimy zatem wpisać minusy. Jeśli A – C ma być niepuste, to coś musi znajdować się w obszarze zbioru A leżącym poza C. Cały czas mamy jednak do wyboru dwie części tego obszaru i nie wiemy do końca, w którą z nich wpisać „+” . Wypełniony według poprzednika implikacji diagram wygląda zatem następująco:

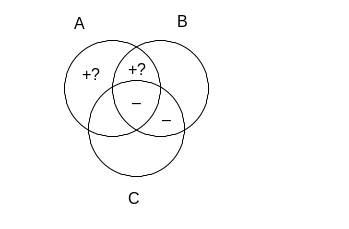
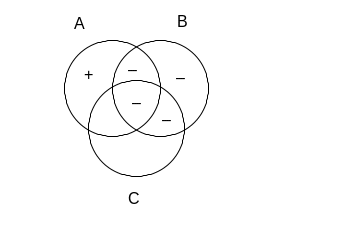
Musimy teraz sprawdzić, czy powyższy rysunek gwarantuje nam, że C’  B  . Część wspólna dopełnienia C oraz B to obszar zbioru B leżący poza C, czyli „górny” półksiężyc zbioru B. W jednej części tego obszaru znajduje się wprawdzie plus, jednak jest on z pytajnikiem, co oznacza, iż nie mamy gwarancji, że jest on tam na pewno. Nie mamy zatem pewności, że następnik badanej implikacji jest prawdziwy, a więc nie jest ona prawem rachunku zbiorów.

Rysunek pokazujący, że pomimo prawdziwości poprzednika, następnik implikacji może być fałszywy, wygląda następująco:

▲

Zależności trudniejsze do zaznaczenia na diagramie.

Przykład:

Sprawdzimy, czy jest prawem rachunku zbiorów wyrażenie:

[A  C  B  A  (B  C)’]  B – C = 

W powyższym przykładzie pewne trudności sprawić może właściwe zaznaczenie na diagramie informacji z poprzednika implikacji. Fakt, że suma zbiorów A i C zawiera się w B oznacza, że żadna część A oraz żadna część C nie może znajdować się poza zbiorem B. We wszystkich fragmentach zbiorów A i C leżących poza B musimy więc wpisać minusy.

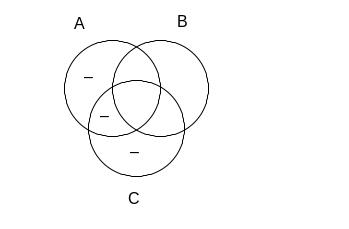
Z kolei to, że A zawiera się w dopełnieniu sumy B i C znaczy, że żadna część zbioru A nie może znajdować się w zbiorze B lub C. W związku z tym w częściach wspólnych A i C oraz A i B musimy wpisać minusy. W jednym fragmencie wymienionego obszaru minus już się znajduje, zatem dodajemy jeszcze dwa:

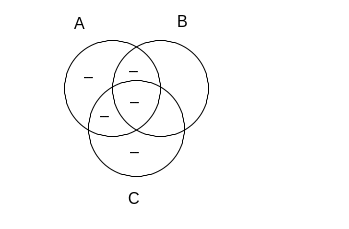
Teraz musimy sprawdzić, czy mamy pewność, że obszar zbioru B leżący poza C (czyli B – C) jest pusty. W jednej części tego obszaru mamy znak „–”, w drugiej natomiast nie ma nic. To, że nie mamy tam wpisanego żadnego symbolu, nie oznacza jednak, ze nic tam nie ma, a jedynie, że nie mamy na temat tej części żadnych informacji. Pewność, że obszar jest pusty, mielibyśmy jedynie wtedy, gdyby umieszczony był w nim minus. Tymczasem nic nie stoi na przeszkodzie, aby w wolne miejsce wpisać plus:

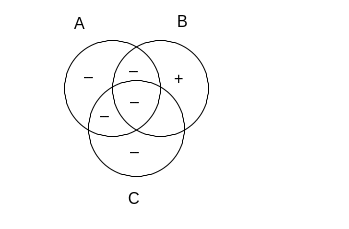
Ponieważ, jak widać na powyższym rysunku, da się wypełnić diagram w ten sposób, aby poprzednik implikacji był prawdziwy, a następnik fałszywy, badane wyrażenie nie jest prawem rachunku zbiorów.

▲

Czasem trzeba zacząć od końca.

Przykład:

Sprawdzimy, czy jest prawem rachunku zbiorów wyrażenie:

(A  B    B  C  )  A  C  

Fakt, że nie jest pusta suma zbiorów A i B, oznacza, że coś musi znajdować się w którejkolwiek części obszaru składającego się aż z sześciu części:

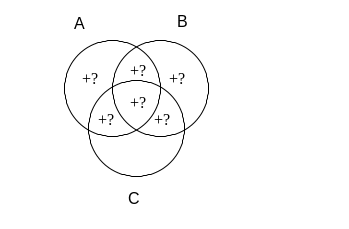
Gdy dodamy to tego informację, że niepusta jest również suma B i C otrzymamy rysunek:

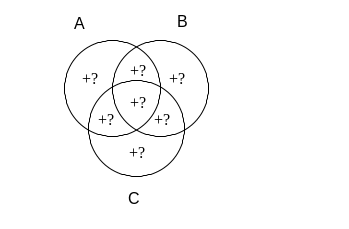
Pozostaje nam teraz odpowiedzieć na pytanie, czy mamy pewność, że coś znajduje się w którejkolwiek części sumy zbiorów A oraz C. Udzielnie jednoznacznej odpowiedzi na to pytanie przy pomocy powyższego rysunku może wydawać się trudne – w wymienionej części znajduje się wprawdzie sześć plusów, ale wszystkie z pytajnikiem. W takiej sytuacji możemy spróbować rozwiązać zadanie niejako od drugiej strony, zaczynając od budowy kontrprzykładu. Zobaczmy, czy da się stworzyć rysunek, na którym następnik implikacji byłby fałszywy, a potem sprawdzimy, czy poprzednik może być wtedy równocześnie prawdziwy.

Fałszywość następnika naszego wyrażenia oznacza, że pusta jest suma zbiorów A i C, czyli:

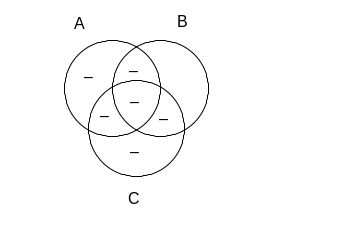
Czy możemy teraz sprawić, aby prawdziwe były oba człony poprzednika implikacji? Stanie się tak, gdy wpiszemy znak „+” w jedyne wolne pole:

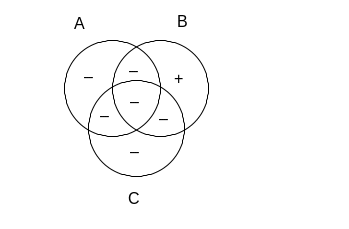
Powyższy rysunek pokazuje, że można zaznaczyć na diagramie jednocześnie prawdziwość poprzednika implikacji (coś znajduje się zarówno w sumie zbiorów A i B jak i w sumie B i C), jak i fałszywość jej następnika (pusta jest suma A i C). Badane wyrażenie nie jest więc prawem rachunku zbiorów.

▲

SŁOWNICZEK:

Dopełnienie zbioru – dopełnienie zbioru A to zbiór zawierający te elementy uniwersum, które nie należą do A.

Identyczność zbiorów – zbiory A i B są identyczne (A = B), gdy mają dokładnie te same elementy.

Iloczyn zbiorów – iloczyn (przekrój) zbiorów A i B (A  B) to zbiór zawierający elementy należące zarówno do A jak i do B.

Inkluzja (zawieranie się zbiorów) – zbiór A zawiera się w zbiorze B (A  B), gdy każdy element A jest elementem B.

Krzyżowanie zbiorów – zbiory A i B się krzyżują (A # B), gdy mają one wspólne elementy, ale równocześnie do każdego z nich należą takie elementy, które nie należą do drugiego.

Rozłączność zbiorów – zbiory A i B są rozłączne (A )( B), gdy nie mając ani jednego wspólnego elementu.

Różnica zbiorów – różnica zbiorów A i B to zbiór zawierający te elementy A, które nie należą do B.

Suma zbiorów – suma zbiorów A i B (A  B) to zbiór powstały z połączenia elementów A i B.

Zbiór pusty – zbiór nie zawierający żadnego elementu. Zbiór pusty oznaczamy symbolem .