4.3.2. Praktyka: Badanie poprawności definicji sprawozdawczych.

Sprawdzanie poprawności definicji sprawozdawczych jest niezwykle proste. Sprowadza się ono do określenia co stanowi definiendum oraz definiens, a następnie zbadania stosunków między nimi.

Przykład:

Sprawdzimy poprawność definicji: Termometr jest to przyrząd do mierzenia.

W definicji tej termin definiowany (definiendum) stanowi nazwa termometr, natomiast termin definiujący (definiens) – przyrząd to mierzenia.

Po narysowaniu diagramu możemy zadać trzy pytania, na które odpowiedzi są oczywiste:

I – czy istnieje termometr, który nie jest przyrządem do mierzenia – nie,

II – czy istnieje termometr, który jest przyrządem do mierzenia – tak,

III – czy istnieje przyrząd do mierzenia, który nie jest termometrem – tak (np. linijka).

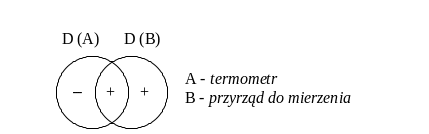
Otrzymany rysunek wskazuje, że definiendum jest podrzędne względem definiensa, a zatem badana definicja jest za szeroka.

To, że badana definicja jest za szeroka widać w zasadzie już na pierwszy rzut oka – zbyt szeroko definiuje ona termometr.

▲

Przykład:

Zbadamy poprawność definicji: Termometr jest to przyrząd do mierzenia temperatury ludzkiego ciała.

Odpowiedzi na odpowiednio zadane pytania są następujące:

I – tak (np. termometr okienny),

II – tak,

III – nie.

Wypełniony zgodnie z tymi odpowiedziami diagram wskazuje na nadrzędność definiendum względem definiensa, a więc badana definicja jest za wąska.

▲

4.3.3. Utrudnienia I pułapki.

Trudno mówić o jakichkolwiek pułapkach przy tak prostych zadaniach, jak sprawdzanie definicji sprawozdawczych. Jedyny kłopot może tu polegać na konieczności wykorzystania czasem wiedzy pozalogicznej potrzebnej do odpowiedzi na pytanie: czy istnieje pewna rzecz A będąca (lub nie będąca) B. Wiedza ta może czasem dotyczyć dziedzin specjalistycznych, obcych osobie badającej poprawność definicji.

Słowniczek.

Definiendum (termin definiowany) – termin, którego znaczenie podaje definicja.

Definiens (termin definiujący) – człon definicji wyjaśniający znaczenie terminu definiowanego.

Denotacja nazwy (zakres nazwy) – zbiór wszystkich desygnatów danej nazwy. Przykładowo zbiór wszystkich studentów jest denotacją (zakresem) nazwy student.

Desygnat nazwy – obiekt oznaczany przez daną nazwę. Na przykład każdy z nas jest desygnatem nazwy człowiek.

Łącznik definicyjny – zwrot łączący definiendum i definiens. Na przykład: jest to, znaczy tyle co itp.

Nazwa abstrakcyjna – nazwa, której desygnaty nie są przedmiotami materialnymi. Na przykład: nienawiść, śmiech, egzamin.

Nazwa generalna – nazwa, która przysługuje przedmiotowi ze względu na jakieś cechy, które temu przedmiotowi przypisujemy. Na przykład: poeta romantyczny, miasto nad Wisłą, student.

Nazwa indywidualna – nazwa przyporządkowana danemu przedmiotowi na mocy arbitralnej decyzji, niezależnie od przysługujących temu przedmiotowi cech. Na przykład: Adam Mickiewicz, Kraków, ta oto książka.

Nazwa jednostkowa – nazwa mające dokładnie jeden desygnat. Na przykład: Pałac Kultury i Nauki w Warszawie, najwyższy szczyt w Tatrach.

Nazwa konkretna – nazwa, której desygnaty są przedmiotami materialnymi lub byłyby takimi, gdyby istniały. Na przykład: książka, krasnoludek.

Nazwa nieostra – nazwa, której zakresu nie da się jednoznacznie i obiektywnie wyznaczyć. Na przykład: wysoki mężczyzna, długie przemówienie, tłum.

Nazwa ogólna – nazwa mająca więcej niż jeden desygnat. Na przykład: człowiek, samochód.

Nazwa ostra – nazwa, której zakres da się jednoznacznie określić. Na przykład: medalista olimpijski, liczba parzysta, student.

Nazwa pusta – nazwa nie mająca ani jednego desygnatu. Na przykład: jednorożec, człowiek o wzroście 3 m.