4.2.3. Praktyka: zastosowanie diagramów venna.

Zależność między dwiema nazwami nie zawsze da się odkryć w tak prosty sposób, jak w powyższych przykładach. W niektórych przypadkach, szczególnie gdy mamy do czynienia z nazwami złożonymi, dobrze jest się posłużyć bardziej wyrafinowanym sposobem – metodą diagramów Venna. Diagramy te omawiane były już przy okazji sprawdzania poprawności sylogizmów. Obecnie ich wykorzystanie będzie na pewno o wiele prostsze.

Badanie zależności między dwiema nawami przy pomocy diagramów Venna rozpoczynamy od narysowania dwóch kół reprezentujących zakresy rozważanych nazw:

Jak widać, diagram taki składa się z trzech obszarów. W obszary te będziemy musieli wpisać znaki „+” lub „–” w zależności od tego, czy coś się w nich znajduje, czy też są one puste.

To, czy w danych obszarach diagramu znajdują się jakieś elementy odkrywamy odpowiadając na trzy proste pytania:

I – czy istnieje A, które nie jest B?

II – czy istnieje A, które jest B?

III – czy istnieje B, które nie jest A?

Przy założeniu, że żadna z nazw nie jest nazwą pustą, możemy otrzymać jeden z następujących rysunków świadczących o zależnościach między badanymi nazwami.

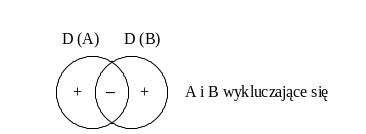
W arto zapamiętać!

Gdyby ktoś miał problemy z zapamiętaniem, który rysunek świadczy o nadrzędności nazwy A względem B, a który o podrzędności, może to sobie utrwalić przy pomocy prostego skojarzenia. Gdy mamy rysunek ze znakiem „+” z jednej strony, a „–” z drugiej, to nadrzędna jest ta nazwa, przy której znajduje się „+”, a podrzędna ta, gdzie mamy „–”.

Powyższe rysunki ilustrują zależności pomiędzy nazwami przy założeniu, że żadna nazwa nie jest pusta. Nazwy puste rzadko bywają wykorzystywane w tego typu zadaniach. Dla porządku jednak dodajmy, że każda nazwa pusta jest podrzędna względem dowolnej nazwy niepustej, natomiast dwie nazwy puste są sobie zawsze równoważne.

Przykład:

Zbadamy zależności między nazwami A – nie-pies, B – nie-wydra.

Po narysowaniu diagramu, w którym jedno koło symbolizuje zakres nazwy nie-pies, a więc zbiór wszystkich obiektów nie będących psami, natomiast drugie zakres nazwy nie-wydra (zbiór wszystkich nie-wydr), zadajemy trzy pytania:

I – czy istnieje nie-pies, który nie jest nie-wydrą? Pytanie to początkowo wydaje się dość zagmatwane, możemy je jednak znacznie uprościć, korzystając z prawa mówiącego, że dwa przeczenia się znoszą. Tak więc, jeśli coś nie jest nie-wydrą, oznacza to, iż jest to po prostu wydrą. W ostatecznej, uproszczonej wersji nasze pytanie brzmi zatem: czy istnieje nie-pies, który jest wydrą? Oczywiście istnieje coś takiego i jest to po prostu wydra. W odpowiednim polu diagramu wpisujemy zatem znak „+”.

II – czy istnieje nie-pies, który jest nie-wydrą? Mówiąc inaczej, czy istnieje coś, co nie jest psem i jednocześnie nie jest wydrą. Oczywiście istnieje bardzo wiele takich rzeczy, na przykład może być to zając, tak więc w środkowym obszarze diagramu wpisujemy znak „+”.

III – czy istnieje nie-wydra, która nie jest nie-psem? Po uproszczeniu tego pytania w taki sam sposób jak w przypadku pytania I otrzymujemy: czy istnieje nie-wydra, która jest psem. Oczywiście istnieje coś takiego – jest to pies. W ostatnią część diagramu również wpisujemy zatem „+”.

Otrzymany rysunek świadczy, iż nazwy nie-pies i nie-wydra się krzyżują.

▲

Przykład:

Zbadamy zależności między nazwami A – nie-ojciec, B – nie-dziadek.

Pytania konieczne do wypełnienia diagramu przestawiają się następująco:

I – czy istnieje nie-ojciec, który nie jest nie-dziadkiem, a więc: czy istnieje nie-ojciec, który jest dziadkiem? Takiej osoby nie ma, ponieważ jeśli ktoś nie jest ojcem, nie może w żaden sposób zostać dziadkiem. W pierwszej części diagramu wpisujmy zatem znak „–”.

II – czy istnieje nie-ojciec, który jest nie-dziadkiem? Taka osoba istnieje, na przykład mężczyzna nie mający dzieci. W środkowej części diagramu wpisujemy znak „+”.

III – czy istnieje nie-dziadek, który nie jest nie-ojcem, a więc: czy istnieje nie-dziadek, który jest ojcem? Taka osoba istnieje – jest to mężczyzna mający dzieci, ale nie mający wnuków. W ostatnie pole diagramu wpisujmy „+”.

Otrzymany rysunek wskazuje, że nazwa nie-ojciec jest podrzędna względem nazwy nie-dziadek lub, jak kto woli, nazwa nie-dziadek jest nadrzędna do nie-ojciec.

▲