2.4. Kwadrat logiczny.

2 .4.1. Łyk teorii.

Omawiane w poprzednich paragrafach sylogizmy to wnioskowania mające zawsze dwie przesłanki. Jednakże zdania kategoryczne (każde S jest P, żadne S nie jest P, niektóre S są P oraz niektóre S nie są P) wykorzystuje się też czasem w tak zwanych wnioskowaniach bezpośrednich – rozumowaniach, w których występuje tylko jedna przesłanka, na podstawie której wyciąga się pewną konkluzję. Poprawność tego rodzaju wnioskowań badać można przy pomocy tak zwanego kwadratu logicznego (omówionego w niniejszym paragrafie) oraz innych praw logiki tradycyjnej (przedstawionych w paragrafie 2.5).

Kwadrat logiczny pokazuje związki logiczne zachodzące pomiędzy zdaniami kategorycznymi. Znajomość tych zależności pozwala stwierdzić, jaka jest wartość logiczna pewnego zdania, na podstawie wartości innego zdania. Przykładowo, wiedząc, że prawdziwe jest zdanie SaP możemy z całkowitą pewnością stwierdzić, że prawdziwe jest również zdanie SiP, natomiast fałszywe SeP oraz SoP.

Zależności w kwadracie logicznym przedstawiane są przy pomocy linii. Każda z tych zależności ma swoją nazwę, która zostanie podana przy odpowiedniej linii.

Kwadrat logiczny wygląda następująco:

przeciwieństwo

SaP

SeP

sprzeczność

SoP

SiP

podprzeciwieństwo

Zależności kwadratu logicznego – podporządkowanie, przeciwieństwo, podprzeciwieństwo i sprzeczność, przedstawimy w postaci odpowiednich wzorów, które, dla wygody w dalszych rozważaniach, ponumerujemy. Znak negacji w tych wzorach, postawiony przed danym zdaniem, będzie wskazywał, że zdanie to jest fałszywe. Przykładowo, wzór: SaP  ~ (SeP) (jeśli SaP to nieprawda, że SeP) odczytamy – prawdziwość zdania SaP implikuje fałszywość SeP (jeśli SaP jest prawdziwe, to SeP jest fałszywe).

Aby prawa kwadratu logicznego miały sens, należy pamiętać o specyficznym rozumieniu zdań SiP oraz SoP. Zdanie niektóre S są P oznacza w tym rozumieniu istnieje (przynajmniej jedno) S będące P. Natomiast niektóre S nie są P – istnieje (przynajmniej jedno) S nie będące P.

Należy również nadmienić, że prawa kwadratu logicznego obowiązują jedynie dla nazw niepustych. Oznacza to, że terminy S oraz P muszą mieć jakieś desygnaty. Nie mogą być to wyrażenia typu: żonaty kawaler, niebieski krasnoludek itp.

Podporządkowanie.

Pionowe linie reprezentują to podporządkowanie. Zależność ta polega na tym, że gdy prawdziwe jest zdanie „górne”, to prawdziwe jest też „dolne”. Symbolicznie:

1) SaP  SiP,

2) SeP  SoP

Na przykład, gdy prawdziwe jest zdanie każda kura jest ptakiem, to prawdziwe jest też niektóre kury są ptakami (lub lepiej: istnieją kury będące ptakami). Gdy prawdziwe jest żadna krowa nie jest ptakiem, to prawdziwe jest też niektóre krowy nie są ptakami (lub lepiej: istnieją krowy nie będący ptakami).

Możemy też powiedzieć, że zdanie „dolne” wynika ze zdania, któremu jest podporządkowane.

Przeciwieństwo.

Pozioma linia na górze pomiędzy SaP oraz SeP to przeciwieństwo. Polega ono na tym, że wymienione zdania nie mogą być zarazem prawdziwe. Czyli, gdy jedno jest prawdziwe, to drugie musi być fałszywe. Symbolicznie:

3) SaP  ~ (SeP),

4) SeP  ~ (SaP)

Na przykład gdy prawdziwe jest zdanie każda papuga jest ptakiem to fałszywe musi być żadna papuga nie jest ptakiem. Natomiast, gdy prawdziwe jest żadna krowa nie jest ptakiem, to fałszywe musi być każda krowa jest ptakiem.

Zdania przeciwne mogą być jednak jednocześnie fałszywe. Przykładowo fałszywe jest zarówno zdanie każda krowa jest czarna oraz żadna krowa nie jest czarna.

W przypadku zdań przeciwnych możemy też powiedzieć, że zdania te się wykluczają.

Podprzeciwieństwo.

Pozioma linia na dole, łącząca zdania SiP oraz SoP, to podprzeciwieństwo. Zdania podprzeciwne nie mogą być zarazem fałszywe. Czyli, gdy jedno jest fałszywe, to drugie musi być prawdziwe. Symbolicznie:

5) ~ (SiP)  SoP

6) ~ (SoP)  SiP

Przykładowo, gdy fałszywe jest zdanie niektóre kanarki są niedźwiedziami, to prawdziwe jest niektóre kanarki nie są niedźwiedziami (lub lepiej: istnieją kanarki nie będące niedźwiedziami). Gdy natomiast fałszywe jest zdanie niektóre żaby nie są płazami, to prawdziwe musi być niektóre żaby są płazami (lub lepiej: istnieją żaby będące płazami).

Zdania podprzeciwne mogą być jednak jednocześnie prawdziwe, przykładowo: niektórzy Polacy są katolikami i niektórzy Polacy nie są katolikami.

W przypadku zdań podprzeciwnych możemy też powiedzieć, że zdania te się dopełniają.

Sprzeczność.

Linie skośne, łączące zdanie SaP z SoP oraz SeP z SiP, reprezentują sprzeczność. Sprzeczność oznacza, że zdania te nie mogą być zarazem ani prawdziwe, ani fałszywe. Mówiąc inaczej, mają one zawsze różną wartość logiczną; gdy jedno prawdziwe, to drugie fałszywe, a gdy jedno fałszywe, to drugie prawdziwe. Symbolicznie:

7) SaP  ~ (SoP)

8) ~ (SaP)  SoP

9) SoP  ~ (SaP)

10) ~ (SoP)  SaP

11) SeP  ~ (SiP)

12) ~ (SeP)  SiP

13) SiP  ~ (SeP)

14) ~ (SiP)  SeP

Przykładowo, jeśli prawdziwe jest zdanie każdy słoń jest ssakiem, to fałszywe musi być niektóre słonie nie są ssakami. Gdy natomiast fałszywe jest zdanie każdy słoń żyje w Afryce, to prawdziwe musi być niektóre słonie nie żyją w Afryce (wzory 7 i 8). Podobne przykłady łatwo podać również w odniesieniu do pozostałych wzorów.

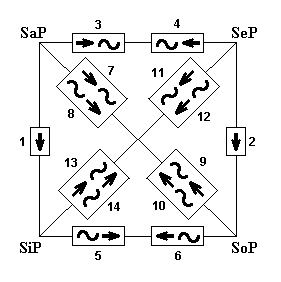
Poniższy rysunek może pomóc w zapamiętaniu wzorów kwadratu logicznego: