Розв'язання

1. Ухвалення рішень в умовах повної невизначеності

Критерій Вальда відповідає песимістичній оцінці: вибирається та альтернатива, для якої песимістична оцінка найбільша, тобто максимум з мінімумів, краща з гірших:

, (2.1)

Так, для матриці цінності (табл. 2.1) отримаємо:

К₁^В = min (200; 80;-100) = -100,

К₂^В = min (100; 30;-40) = -40,

K₃^В = min (20; 10; -10) = -10,

і^В = arg max (-100; -40; -10) = 3.

При цьому К^В =-10.

Згідно максимаксному критерію вибирається альтернатива з найбільшою оптимістичною оцінкою (краща з кращих):

, (2.2)

У даному випадку:

К₁^М = max (200; 80;-100) = 200,

К₂^М = max (100; 30;-40) = 100,

K₃^М = max (20; 10; -10) = 20,

і^М = arg max (200; 100; 10) = 1.

При цьому К^М = 200.

Згідно критерію Гурвіця вибирається коефіцієнт оптимізму 0 ≤ α ≤ 1. Альтернативи оцінюються згідно виразу:

, (2.3)

Виберемо коефіцієнт оптимізму α = 0,3. Тоді за даними даного прикладу отримаємо:

К₁^Г = 0,3 ∙ 200 + 0,7 ∙ (-100) = -10,

К₂^Г = 0,3 ∙ 100 + 0,7 ∙ (-40) = 2,

К₃^Г = 0,3 ∙ 20 + 0,7 ∙ (-10) =-1,

і^Г = arg max (-10;2;-1)= 2.

При цьому К^Г = 2.

Згідно критерію Севіджа спочатку розраховується матриця жалю (звана також матрицею ризиків, матрицею упущеної вигоди):

(2.4)

Альтернативи оцінюються згідно виразу:

(2.5)

Згідно даним даного прикладу матриця жалю має вигляд:

.

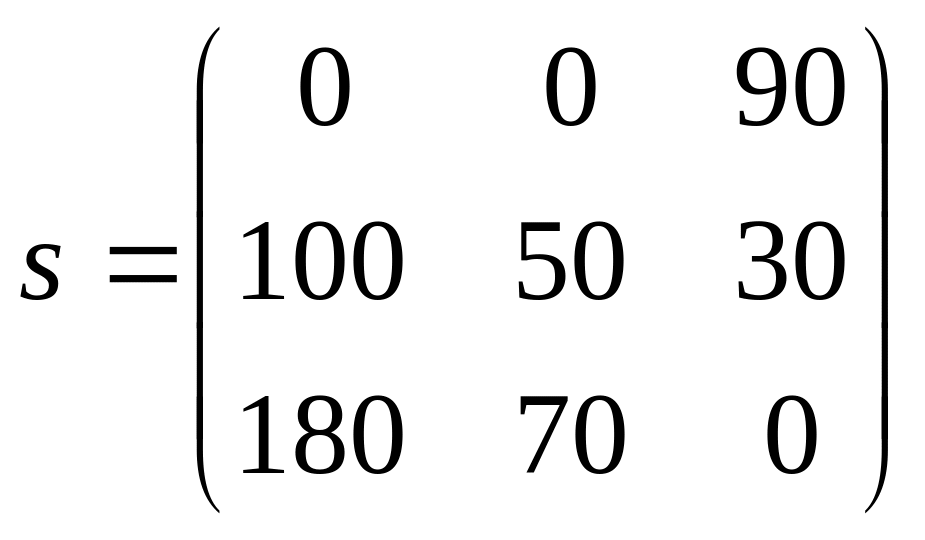Тоді і^С = arg min (180;70;90) = 1.

При цьому К^С = 180.

Результати розрахунку критеріїв зведені в таблицю (табл.2.2). Кращі значення кожного з критеріїв відмічені підкресленням.

Таблиця 2.2. –

Номери альтернативних рішень	Стани зовнішнього середовища			Критерії
	1	2	3	Вальда	Максимаксний	Гурвіця (α = 0,3)	Севіджа
1	200	80	-100	-100	200	-10	180
2	100	30	-40	-40	100	2	70
3	20	10	-10	-10	20	-1	90

2.Ухвалення рішень в умовах часткової невизначеності.

Якщо яким-небудь чином (наприклад, експертним методом) оцінена вірогідність станів зовнішнього середовища (р_j), то їх використання дозволяє точніше оцінити варіанти наявних альтернативних рішень.

Критерій Байєса-Лапласа рівний математичному очікуванню прибутку. Вибирається та альтернатива, для якої значення критерію максимальне:

, (2.6)

Так, якщо для вірогідності станів зовнішнього середовища даного прикладу складають, то значення критерію будуть рівні:

К₁^БЛ = 200∙0,1+80∙0,5+(-100)∙0,4=20,

К₂^БЛ =100∙0,1+30∙0,5+(-40)∙0,4=9,

К₃^БЛ =20∙0,1+10∙0,5+(-10)∙0,4=3.

Отже, краще рішення - перше (і^БЛ = arg max (20; 9; 3) = 1, К^БЛ =20).

Критерій Ходжеса-лемана дозволяє врахувати можливість помилки прогнозу експертами значень вірогідності стратегій зовнішнього середовища.

Задається коефіцієнт довіри 0 ≤ β ≤ 1. Критерій має вигляд:

К_і^ХЛ = βК_і^БЛ + (1-β)К_і^В, і^ХЛ = argmax (К_і^ХЛ). (2.7)

Якщо вибрати, то отримаємо:

К₁^ХЛ = 0,8 ∙ 20 + 0,2 ∙ (-100) = -4,

К₂^ХЛ = 0,8 ∙ 9 + 0,2 ∙ (-40) = -0,8,

К₃^ХЛ = 0,8 ∙ 3 + 0,2 ∙ (-10) = 0,4.

і^ХЛ = argmax (-4;-0,8; 0,4) = 3. При цьому К^ХЛ = 0,4.

Результати розрахунку критеріїв зведені в таблицю (табл.2.3). Кращі значення кожного з критеріїв відмічені підкресленням.

Таблиця 2.3. -

Альтернативні рішення	Стани зовнішнього середовища			Критерії
	1	2	3	Вальда	Байеса-Лапласа	Ходжеса-лемана (β = 0,8)
Рішення 1	200	80	-100	-100	20	-4
Рішення 2	100	30	-40	-40	9	-0,8
Рішення 3	20	10	-10	-10	3	0,4