4. Уточнение корней уравнений методом простой итерации Необходимые сведения из теории

4.1. Методы отделения корней уравнений

Чем меньше длина отрезка изоляции, тем выше точность прибли­жения, однако с помощью используемых для отделения корней при­емов получить отрезок достаточно малой длины трудно. Нуж­ны специальные методы уточнения корней. Далее в главе будет рас­смотрено несколько таких методов, которые реализуют следующие два способа поиска приближенного корня с заданной точностью ε > 0:

1. Последовательно уменьшая длины отрезка изоляции корня по какому-либо правилу, отыскивается отрезок такой, что 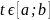и 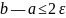. Тогда приближенным корнем требуемой точности бу­дет середина отрезка

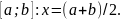
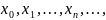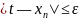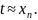2. Строится последовательность чисел сходящая­ся к корню t. Как только окажется , можно положить Такая последовательность называется последовательностью прибли­жений, а определяющий ее метод — методом последовательных при­ближений.

Первый способ удобен тем, что позволяет легко устанавливать завершение процесса уточнения, поскольку отрезки изоляции и их длины на каждом шаге вычислений известны.

Непосредственную проверку условия из второго спо­соба проводить не удается, ибо неизвестен точный корень t. В то же время для каждого метода последовательных приближений есть воз­можность получить неравенства вида

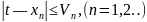
Здесь V_n — числовое выражение, значения которого при каждом η характеризуют степень близости приближения к корню, обес­печиваемую данным методом. За условие окон­чания процесса приближений можно взять неравенство: .

Абсолют­ной погрешность каждого приближения ибо ясно, что

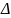
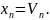
4.2. Алгоритм построения итерационной последовательности, по­рождаемой уравнением )

Рассмотрим уравнение вида х=g(х)с корнем t, отделенным на отрезке . Функция g предполагается непрерывной на этом отрезке. Уравнение х=g(х)можно получить из уравнения f(x) = 0 путем эквивалентных преобразований. Метод простой итерации является одним из наиболее удобных и эффективных методов приближенного решения уравнений, он предполагает уточнение корня с исполь­зованием итерационной последовательности.

Рекуррентная формула определяется на основе самого уравне­ния х=g(х).Если известен какой-либо член последовательности 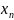(например, 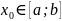), то за , можно взять . Соотношение 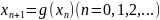является искомой рекуррентной формулой.

4.3. Достаточное условие сходимости итерационной последова­тельности

Пусть корень t уравнения х=g(х) отделен на отрезке длины h. Если на отрезке 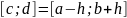функция g дифференцируема и найдется число 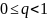такое, что 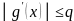при всех 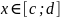, то итерационная последовательность, порожденная формулой х=g(х), сходится к корню t при любом выборе начального приближения

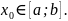
4.4. Оценка погрешности n-го приближения к корню

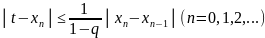
На каждом шаге метода простой итерации можно определить аб­солютную погрешность приближения :

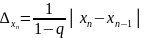
где .

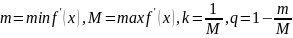4.5. Условие окончания итерационного процесса при заданной до­пустимой погрешности

Таким образом, если задана точность приближенного корня ε > 0, то итерационный процесс необходимо закончить при выполнении условия

где ;

и взять .

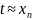4.6. Способы приведения уравнения к равносильному урав­нению х= φ(х) с требуемыми для метода свойствами

Способ 1. Если 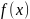содержит в себе выражение некоторой об­ратимой на 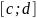функции 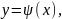причем такой, что 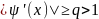на , то следует попытаться заменить уравнение f(x) = 0 на равно­сильное вида х=g(х)с использованием обратной для ψ функции φ: 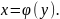Этот способ основан на известном соотношении между про­изводными взаимообратных функций и следствии из него: если то .

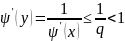Способ 2. В случае когда способ 1 применить трудно или он не дает нужного результата, можно использовать следующий способ.

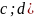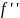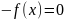Пусть дано уравнение f(x) = 0 с единственным корнем в . Пред­положим, что на отрезке [ производ­ная функции непрерывна, не равна константе, и принимает зна­чения одного и того же знака. Будем считать, что f'(x) > 0, ибо в противном случае можно рассматривать равносильное уравнение: . Тогда

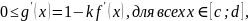
где .
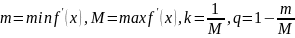