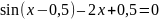- •Міністерство освіти і науки України Національний технічний університет України "Київський політехнічний інститут"
- •Розрахунково-графічна робота з курсу «Обчислювальна математика»
- •Содержание
- •1. Вычисления с учетом погрешностей Необходимые сведения из теории
- •1.1 Абсолютная и относительная погрешности приближенных
- •Чисел и правило их записи.
- •1.2. Верные значащие цифры приближенных чисел.
- •1.3. Нахождение абсолютной погрешности по верным цифрам
- •1.4. Правило округления чисел
- •1.5. Правило записи приближенных чисел
- •1.6. Оценка влияния погрешностей аргументов на значение функции
- •1.7. Оценка погрешностей арифметических действий
- •Задание
- •2. Метод половинного деления Необходимые сведения из теории
- •2.1. Этапы приближенного решения уравнений с одним неизвестным
- •2.2. Отделение корней. Графическое отделение корней
- •2.3. Условия применения метода половинного деления
- •2.4. Алгоритм метода половинного деления
- •2.5. Условие окончания процесса деления при заданной допустимой погрешности
- •Задание
- •3. Комбинированный метод хорд и касательных
- •3.5. Условие окончания процесса вычислений при заданной допустимой погрешности
- •Задание
- •4. Уточнение корней уравнений методом простой итерации Необходимые сведения из теории
- •4.1. Методы отделения корней уравнений
- •4.2. Алгоритм построения итерационной последовательности, порождаемой уравнением )
- •4.3. Достаточное условие сходимости итерационной последовательности
- •4.4. Оценка погрешности n-го приближения к корню
- •4.5. Условие окончания итерационного процесса при заданной допустимой погрешности
- •Задание
- •5. Метод простой итерации приближенного решения систем линейных алгебраических уравнений Необходимые сведения из теории
- •5.1. Способы определения расстояния в пространстве Rn
- •5.2. Абсолютная погрешность числового вектора и его координат
- •5.3. Сходимость последовательности векторов в Rn
- •5.4. Приведенная система уравнений. Cпособы преобразования систем к приведенному виду
- •5.5. Построение итерационной последовательности
- •6. Интерполирование математических таблиц Необходимые сведения из теории
- •6.1. Табличная функция
- •6.2. Задача интерполирования табличной функции
- •6.3. Теорема о единственности задачи полиномиального интерполирования
- •6.4. Конечные разности таблиц
- •6.5. Первый и второй интерполяционные многочлены Ньютона. Оценка погрешностей интерполяционных формул Ньютона
- •6.6. Формула линейного интерполирования и способы оценки ее погрешности
- •6.7. Обратное линейное интерполирование
- •Задание
- •Квадратичное приближение табличных функций по методу наименьших квадратов Необходимые сведения из теории
- •Задача аналитического приближения табличных функций
- •Задача приближения по методу наименьших квадратов
- •7.3. Алгоритм построения наилучшего многочлена по данному методу
- •7.4. Уклонения, среднеквадратичное уклонение
- •Задание
- •Задание по вариантам
- •Порядок выполнения работы
- •8. Приближенное вычисление определенных интегралов Необходимые сведения из теории
- •8.1. Численный метод приближенного вычисления определенных интегралов
- •8.2. Квадратурные формулы трапеций и Симпсона
- •8.3. Строгая оценка погрешностей этих формул
- •8.4. Оценка погрешностей методом двойного пересчета
- •8.5. Определение шага разбиения отрезка интегрирования, при котором квадратурная формула обеспечивает заданную точность
- •8.6. Вопросы оценки точности приближенного интеграла с учетом вычислительных погрешностей
- •Задание
- •Численное решение обыкновенных дифференциальных уравнений методом эйлера-коши Необходимые сведения из теории
- •Общее и частное решения обыкновенного дифференциального уравнения 1-го порядка. Интегральные кривые
- •Задача Коши. Теорема Пикара
- •Геометрический смысл правой части дифференциального уравнения, разрешенного относительно производной
- •Понятие численного решения. Ломаная Эйлера
- •Метод Эйлера- Коши, его геометрический смысл
- •Оценка погрешности численного решения методом двойного пересчета
- •Задание
- •Порядок выполнения работы
- •Использованная литература:
2.4. Алгоритм метода половинного деления
П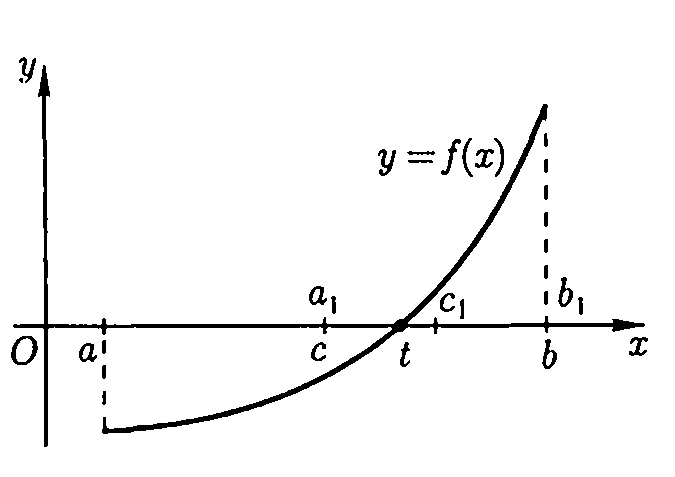
Рис.3
усть f непрерывна на и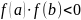 .
Разделим
пополам
точкой
.
Разделим
пополам
точкой
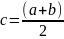 и вычислим f(с).
Если f(с)
= 0, то корень t
найден точно (а именно,
и вычислим f(с).
Если f(с)
= 0, то корень t
найден точно (а именно,
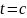 ).
Если
же нет, выберем ту половину отрезка, на
концах которой значения функции
разных знаков, и обозначим ее [а1;
b1]
(на рис. 3 правая половина
).
Затем
отрезок [а1;
b1]
делим пополам точкой
).
Если
же нет, выберем ту половину отрезка, на
концах которой значения функции
разных знаков, и обозначим ее [а1;
b1]
(на рис. 3 правая половина
).
Затем
отрезок [а1;
b1]
делим пополам точкой
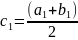 и
проводим аналогичные рассуждения.
Получится либо точный корень с1,
либо отрезок [а2;
b2]
со
свойством
и
проводим аналогичные рассуждения.
Получится либо точный корень с1,
либо отрезок [а2;
b2]
со
свойством
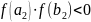 .
.
И так далее, пока функция от сn не будет равна нулю (или пока не будет выполняться условие окончания процесса при заданной погрешности).
2.5. Условие окончания процесса деления при заданной допустимой погрешности
Для того чтобы найти приближенное значение корня с точностью до ε > 0, необходимо остановить процесс половинного деления па таком шаге n, на котором отрезок [аn ; bn], будет иметь длину
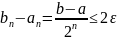
и
вычислить
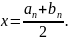 Тогда
можно взять
,
причем
Тогда
можно взять
,
причем
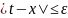 .
.
Задание
Отделите
корни данного уравнения и уточните их
методом половинного деления с
точностью до
ε
= 0,5
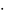 10-4.
10-4.
Вариант |
Уравнение |
10 |
|
1. Отделим графически все корни уравнения f(x) = 0 так, чтобы на отрезках изоляции корней функция f удовлетворяла условиям метода половинного деления.
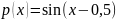
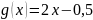
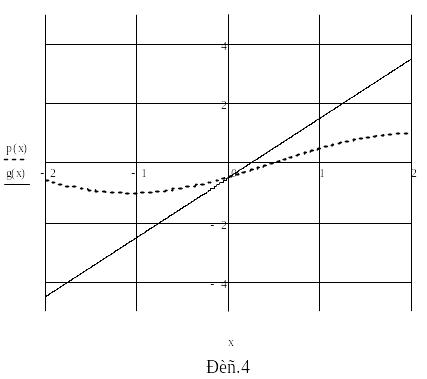
Из
графика примем
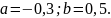
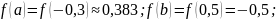
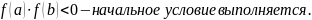
2. Выполним один шаг метода для одного из корней вручную и проверим условие окончания вычислений.
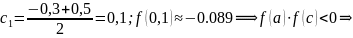

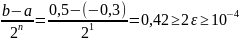
3. Составим программу уточнения корня с точностью до ε, выводящую в таблицу номер итерации, концы вложенных отрезков и их длины.
Текст программы:
var
x,y,x0,x1: real;
e,a,dlina,b: real;
l,n,i:integer;
function f(x: real):real;
begin
f:=(sin(x-0.5))-2*x+0.5;
end;
begin
a:=-0.3;
b:=0.5;
write('e=');
readln(e);
x0:=a;
x1:=b;
while true do
begin
x:=(x0+x1)/2;
y:=f(x);
l:=1;
n:=n+1;
dlina:=(x1-x0)/l;
if dlina<e then
begin
writeln('x=',x:1:6);
break
end
else
begin
for i:=1 to n do l:=l*2;
if y*f(x0)>0 then x0:=x
else x1:=x;
writeln ('[',x0:1:6,';',x1:1:6,'] ',
'iteracia #', n,
' ',
'dlina otrezka',
' ',
dlina:1:4);
end
end;
readln
end.
Результат, выведенный на экран:
e=0.00005
[-0.300000;0.100000] iteracia #1 dlina otrezka 0.8000
[-0.100000;0.100000] iteracia #2 dlina otrezka 0.4000
[-0.000000;0.100000] iteracia #3 dlina otrezka 0.2000
[-0.000000;0.050000] iteracia #4 dlina otrezka 0.1000
[-0.000000;0.025000] iteracia #5 dlina otrezka 0.0500
[0.012500;0.025000] iteracia #6 dlina otrezka 0.0250
[0.012500;0.018750] iteracia #7 dlina otrezka 0.0125
[0.015625;0.018750] iteracia #8 dlina otrezka 0.0063
[0.017187;0.018750] iteracia #9 dlina otrezka 0.0031
[0.017969;0.018750] iteracia #10 dlina otrezka 0.0016
[0.018359;0.018750] iteracia #11 dlina otrezka 0.0008
[0.018359;0.018555] iteracia #12 dlina otrezka 0.0004
[0.018359;0.018457] iteracia #13 dlina otrezka 0.0002
[0.018359;0.018408] iteracia #14 dlina otrezka 0.0001
x=0.018384
4. Найдите все приближенные корни уравнения и выпишите их с верными значащими цифрами.
Ответ:
у уравнения sin(x
-
0,5)– 2x+0,5
= 0 один
корень на
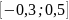 ,
который был вычислен с точностью ε = 0,5
10-4
:
,
который был вычислен с точностью ε = 0,5
10-4
:
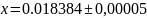 ;
;