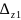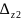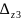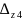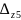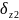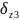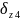- •Міністерство освіти і науки України Національний технічний університет України "Київський політехнічний інститут"
- •Розрахунково-графічна робота з курсу «Обчислювальна математика»
- •Содержание
- •1. Вычисления с учетом погрешностей Необходимые сведения из теории
- •1.1 Абсолютная и относительная погрешности приближенных
- •Чисел и правило их записи.
- •1.2. Верные значащие цифры приближенных чисел.
- •1.3. Нахождение абсолютной погрешности по верным цифрам
- •1.4. Правило округления чисел
- •1.5. Правило записи приближенных чисел
- •1.6. Оценка влияния погрешностей аргументов на значение функции
- •1.7. Оценка погрешностей арифметических действий
- •Задание
- •2. Метод половинного деления Необходимые сведения из теории
- •2.1. Этапы приближенного решения уравнений с одним неизвестным
- •2.2. Отделение корней. Графическое отделение корней
- •2.3. Условия применения метода половинного деления
- •2.4. Алгоритм метода половинного деления
- •2.5. Условие окончания процесса деления при заданной допустимой погрешности
- •Задание
- •3. Комбинированный метод хорд и касательных
- •3.5. Условие окончания процесса вычислений при заданной допустимой погрешности
- •Задание
- •4. Уточнение корней уравнений методом простой итерации Необходимые сведения из теории
- •4.1. Методы отделения корней уравнений
- •4.2. Алгоритм построения итерационной последовательности, порождаемой уравнением )
- •4.3. Достаточное условие сходимости итерационной последовательности
- •4.4. Оценка погрешности n-го приближения к корню
- •4.5. Условие окончания итерационного процесса при заданной допустимой погрешности
- •Задание
- •5. Метод простой итерации приближенного решения систем линейных алгебраических уравнений Необходимые сведения из теории
- •5.1. Способы определения расстояния в пространстве Rn
- •5.2. Абсолютная погрешность числового вектора и его координат
- •5.3. Сходимость последовательности векторов в Rn
- •5.4. Приведенная система уравнений. Cпособы преобразования систем к приведенному виду
- •5.5. Построение итерационной последовательности
- •6. Интерполирование математических таблиц Необходимые сведения из теории
- •6.1. Табличная функция
- •6.2. Задача интерполирования табличной функции
- •6.3. Теорема о единственности задачи полиномиального интерполирования
- •6.4. Конечные разности таблиц
- •6.5. Первый и второй интерполяционные многочлены Ньютона. Оценка погрешностей интерполяционных формул Ньютона
- •6.6. Формула линейного интерполирования и способы оценки ее погрешности
- •6.7. Обратное линейное интерполирование
- •Задание
- •Квадратичное приближение табличных функций по методу наименьших квадратов Необходимые сведения из теории
- •Задача аналитического приближения табличных функций
- •Задача приближения по методу наименьших квадратов
- •7.3. Алгоритм построения наилучшего многочлена по данному методу
- •7.4. Уклонения, среднеквадратичное уклонение
- •Задание
- •Задание по вариантам
- •Порядок выполнения работы
- •8. Приближенное вычисление определенных интегралов Необходимые сведения из теории
- •8.1. Численный метод приближенного вычисления определенных интегралов
- •8.2. Квадратурные формулы трапеций и Симпсона
- •8.3. Строгая оценка погрешностей этих формул
- •8.4. Оценка погрешностей методом двойного пересчета
- •8.5. Определение шага разбиения отрезка интегрирования, при котором квадратурная формула обеспечивает заданную точность
- •8.6. Вопросы оценки точности приближенного интеграла с учетом вычислительных погрешностей
- •Задание
- •Численное решение обыкновенных дифференциальных уравнений методом эйлера-коши Необходимые сведения из теории
- •Общее и частное решения обыкновенного дифференциального уравнения 1-го порядка. Интегральные кривые
- •Задача Коши. Теорема Пикара
- •Геометрический смысл правой части дифференциального уравнения, разрешенного относительно производной
- •Понятие численного решения. Ломаная Эйлера
- •Метод Эйлера- Коши, его геометрический смысл
- •Оценка погрешности численного решения методом двойного пересчета
- •Задание
- •Порядок выполнения работы
- •Использованная литература:
1.5. Правило записи приближенных чисел
В промежуточных результатах вычислений обычно сохраняются одна-две сомнительные цифры, а окончательные результаты округляют с сохранением не более одной сомнительной цифры.
Первая рекомендация позволяет избегать накопления погрешностей округлений в верных разрядах. Пели вычислений немного, достаточно одной запасной цифры. Напротив, при больших расчетах иногда оказывается оправданным сохранение в промежуточных результатах трех таких цифр.
В ответах часто оставляют только верные цифры. Это удобно, так как по записи числа сразу видно, какие цифры у него верные. Однако здесь надо учесть то, что при округлении некоторых приближенных чисел до верных цифр последняя цифра может оказаться верной лишь в нестрогом смысле, ибо тогда к погрешности числа прибавляется погрешность округления. Тогда ради сохранения качества последней верной цифры целесообразно записывать ответы с дополнительной цифрой. Лишнюю цифру следует оставлять и в том случае, когда известно, что она могла оказаться сомнительной из-за заведомо грубых оценок.
1.6. Оценка влияния погрешностей аргументов на значение функции
Пусть
числа
a,
b
являются приближениями к точным
аргументам А,
В с абсолютными погрешностями
Δа
,
Δb
и
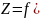 В),
z=
f(a,b).
Если функция
f
дифференцируема в точке (a,b),
то
В),
z=
f(a,b).
Если функция
f
дифференцируема в точке (a,b),
то
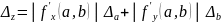
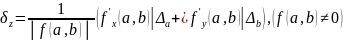
1.7. Оценка погрешностей арифметических действий
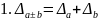
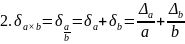
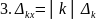

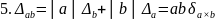
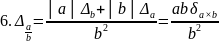
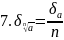
Задание
Пусть а,b,у — приближенные числа с верными в строгом смысле значащими цифрами, х — точное число. Вычислите
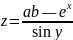
и оцените погрешность результата. Для вычисления значений функций еx и sin у используйте либо математические таблицы, либо микрокалькулятор, либо компьютер.
Вариант |
а |
b |
x |
y |
10 |
2,410 |
-0,794 |
2,019 |
1,96 |
1. Заполним первую таблицу, определив абсолютные погрешности исходных данных по известным верным значащим цифрам, использовав формулу (2) :
а |
2,410 |
b |
-0,794 |
x |
2,019 |
y |
1,96 |
Δа |
0,0005 |
Δb |
0,0005 |
Δx |
0 |
Δy |
0,005 |
δа |
0,00021 |
δb |
0,00063 |
δx |
0 |
δy |
0,0026 |
2.
Оценим погрешности
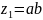 ,
взяв
для этого две-три значащие цифры
произведения. Затем найдем верные
значащие цифры
,
взяв
для этого две-три значащие цифры
произведения. Затем найдем верные
значащие цифры
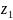 и
запишем ответ с одной сомнительной
цифрой.
и
запишем ответ с одной сомнительной
цифрой.
z1 |
-1,9135 |
z2 |
7,531 |
z3 |
-9,445 |
z4 |
0,925 |
z5 |
-10,2108 |
|
0,0016077 |
|
0,0005 |
|
0,002107 |
|
0,001895 |
|
0,0231948 |
|
0,00084 |
|
0,0000663 |
|
0,000223 |
|
0,0020486 |
|
0,0022716 |
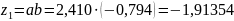
Возьмем
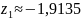 .
Тогда:
.
Тогда:
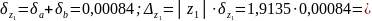
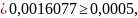
что
говорит о том, что в произведении три
верные цифры после запятой
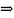
 .
.
3.
Вычислим
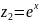 и
округлим его при необходимости так,
чтобы погрешность округления не
оказала существенного влияния на
точность дальнейших расчетов.
и
округлим его при необходимости так,
чтобы погрешность округления не
оказала существенного влияния на
точность дальнейших расчетов.
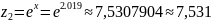
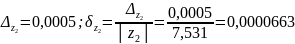
4.
Продолжим вычисления, после чего заполним
вторую таблицу, найдем
 и оценим погрешность результата.
и оценим погрешность результата.
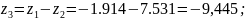
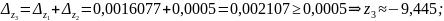
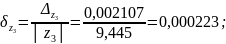
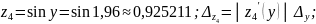

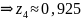
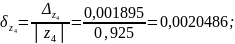
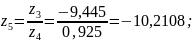
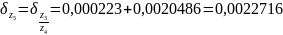
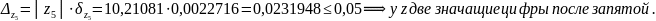
Ответ:
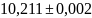 .
.