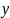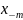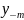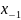- •Міністерство освіти і науки України Національний технічний університет України "Київський політехнічний інститут"
- •Розрахунково-графічна робота з курсу «Обчислювальна математика»
- •Содержание
- •1. Вычисления с учетом погрешностей Необходимые сведения из теории
- •1.1 Абсолютная и относительная погрешности приближенных
- •Чисел и правило их записи.
- •1.2. Верные значащие цифры приближенных чисел.
- •1.3. Нахождение абсолютной погрешности по верным цифрам
- •1.4. Правило округления чисел
- •1.5. Правило записи приближенных чисел
- •1.6. Оценка влияния погрешностей аргументов на значение функции
- •1.7. Оценка погрешностей арифметических действий
- •Задание
- •2. Метод половинного деления Необходимые сведения из теории
- •2.1. Этапы приближенного решения уравнений с одним неизвестным
- •2.2. Отделение корней. Графическое отделение корней
- •2.3. Условия применения метода половинного деления
- •2.4. Алгоритм метода половинного деления
- •2.5. Условие окончания процесса деления при заданной допустимой погрешности
- •Задание
- •3. Комбинированный метод хорд и касательных
- •3.5. Условие окончания процесса вычислений при заданной допустимой погрешности
- •Задание
- •4. Уточнение корней уравнений методом простой итерации Необходимые сведения из теории
- •4.1. Методы отделения корней уравнений
- •4.2. Алгоритм построения итерационной последовательности, порождаемой уравнением )
- •4.3. Достаточное условие сходимости итерационной последовательности
- •4.4. Оценка погрешности n-го приближения к корню
- •4.5. Условие окончания итерационного процесса при заданной допустимой погрешности
- •Задание
- •5. Метод простой итерации приближенного решения систем линейных алгебраических уравнений Необходимые сведения из теории
- •5.1. Способы определения расстояния в пространстве Rn
- •5.2. Абсолютная погрешность числового вектора и его координат
- •5.3. Сходимость последовательности векторов в Rn
- •5.4. Приведенная система уравнений. Cпособы преобразования систем к приведенному виду
- •5.5. Построение итерационной последовательности
- •6. Интерполирование математических таблиц Необходимые сведения из теории
- •6.1. Табличная функция
- •6.2. Задача интерполирования табличной функции
- •6.3. Теорема о единственности задачи полиномиального интерполирования
- •6.4. Конечные разности таблиц
- •6.5. Первый и второй интерполяционные многочлены Ньютона. Оценка погрешностей интерполяционных формул Ньютона
- •6.6. Формула линейного интерполирования и способы оценки ее погрешности
- •6.7. Обратное линейное интерполирование
- •Задание
- •Квадратичное приближение табличных функций по методу наименьших квадратов Необходимые сведения из теории
- •Задача аналитического приближения табличных функций
- •Задача приближения по методу наименьших квадратов
- •7.3. Алгоритм построения наилучшего многочлена по данному методу
- •7.4. Уклонения, среднеквадратичное уклонение
- •Задание
- •Задание по вариантам
- •Порядок выполнения работы
- •8. Приближенное вычисление определенных интегралов Необходимые сведения из теории
- •8.1. Численный метод приближенного вычисления определенных интегралов
- •8.2. Квадратурные формулы трапеций и Симпсона
- •8.3. Строгая оценка погрешностей этих формул
- •8.4. Оценка погрешностей методом двойного пересчета
- •8.5. Определение шага разбиения отрезка интегрирования, при котором квадратурная формула обеспечивает заданную точность
- •8.6. Вопросы оценки точности приближенного интеграла с учетом вычислительных погрешностей
- •Задание
- •Численное решение обыкновенных дифференциальных уравнений методом эйлера-коши Необходимые сведения из теории
- •Общее и частное решения обыкновенного дифференциального уравнения 1-го порядка. Интегральные кривые
- •Задача Коши. Теорема Пикара
- •Геометрический смысл правой части дифференциального уравнения, разрешенного относительно производной
- •Понятие численного решения. Ломаная Эйлера
- •Метод Эйлера- Коши, его геометрический смысл
- •Оценка погрешности численного решения методом двойного пересчета
- •Задание
- •Порядок выполнения работы
- •Использованная литература:
Задача Коши. Теорема Пикара
Задача нахождения частного решения уравнения , удовлетворяющего начальному условию у=у0 и x=х0, называется задачей Коши.
Задачу
Коши можно решить без выявления общего
решения. Если же общее решение известно
и начальное условие дано, то число С0,
определяющее искомое частное решение,
находят из уравнения относительно
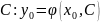 .
.
Геометрический смысл задачи Коши заключается в нахождении интегральной кривой, проходящей через начальную точку (х0, у0).
Прежде чем приступать к решению задачи Коши, предварительно надо выяснить, существует ли решение уравнения, удовлетворяющее данному начальному условию, а если да, то сколько их может быть. Справедлива следующая теорема (теорема Пикара): пусть точка (х0, у0) является внутренней точкой замкнутой прямоугольной области

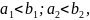 и
на области
D
выполнены условия:
и
на области
D
выполнены условия:
1) функция f непрерывна как функция двух переменных;
2) частная производная f'y существует и ограничена как функция двух переменных (в частности, непрерывна в этой области).
Тогда
найдется такой отрезок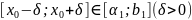 ,
на
котором уравнение
имеет
единственное решение
удовлетворяющее
заданному начальному условию.
,
на
котором уравнение
имеет
единственное решение
удовлетворяющее
заданному начальному условию.
В
качестве начальной точки в теореме
Пикара можно взять любую внутреннюю
точку области
D.
Следовательно,
через каждую такую точку в достаточно
малой ее окрестности проходит
единственная интегральная кривая из
семейства
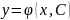 .
.
Геометрический смысл правой части дифференциального уравнения, разрешенного относительно производной
Возьмем
произвольную точку
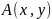 на
интегральной кривой
на
интегральной кривой
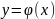 (рис. 9).
Так как функция
φ
является решением, справедливо
соотношение
(рис. 9).
Так как функция
φ
является решением, справедливо
соотношение
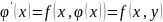
С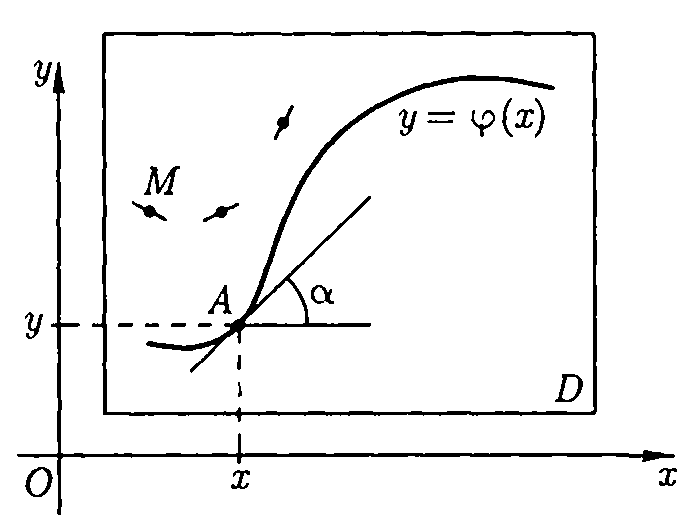
Рис.9
другой стороны, по геометрическому смыслу производной,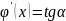 ,
где
α
— угол между касательной, проведенной
к данной кривой в точке А,
и
положительным направлением оси Ох.
Отсюда
следует, что
,
где
α
— угол между касательной, проведенной
к данной кривой в точке А,
и
положительным направлением оси Ох.
Отсюда
следует, что
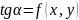 ,
т.е.
значение
f(x,у)
функции
f
равно угловому коэффициенту
касательной, проведенной в точке А
к интегральной кривой
.
,
т.е.
значение
f(x,у)
функции
f
равно угловому коэффициенту
касательной, проведенной в точке А
к интегральной кривой
.
Полученный
результат справедлив для любой
внутренней точки М(х,у)
из
области
D.
Вычислив
 получим
угловой коэффициент касательной к
некоторой проходящей через эту точку
интегральной кривой, при этом сама
кривая может быть неизвестна. Можно
сказать, что значения
получим
угловой коэффициент касательной к
некоторой проходящей через эту точку
интегральной кривой, при этом сама
кривая может быть неизвестна. Можно
сказать, что значения
 определяют
направления
интегральных кривых в
тех точках, где они вычислены.
определяют
направления
интегральных кривых в
тех точках, где они вычислены.
Направление
кривой в точке М(х,у)
обычно
указывается с помощью отрезка
небольшой длины с центром в
Μ
и
с углом наклона
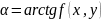 к
положительному направлению оси Ох.
Проведя
достаточно большое число таких отрезков,
получаем некоторое представление
о конфигурации интегральных кривых
уравнения.
к
положительному направлению оси Ох.
Проведя
достаточно большое число таких отрезков,
получаем некоторое представление
о конфигурации интегральных кривых
уравнения.
Понятие численного решения. Ломаная Эйлера
|
|
|
|
|
|
|
|
|
|
|
|
|
|
… |
… |
|
|
Табл.2 |
|
На
практике наиболее распространенными
являются численные
методы приближенного
интегрирования дифференциальных
уравнений, дающие решение задачи
Коши в виде таблицы приближенных
значений точного решения
φ.
Эту таблицу [таблично заданную
функцию
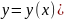 и
называют численным
решением задачи Коши. Для
выполнения начального условия таблица
должна содержать данные х0,
у0.
и
называют численным
решением задачи Коши. Для
выполнения начального условия таблица
должна содержать данные х0,
у0.
|
|
|
|
|
|
|
|
… |
… |
|
|
Табл.3 |
|
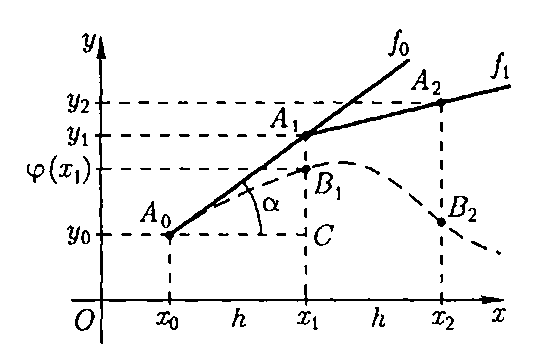
Рис.10
сли задан конечный промежуток, на котором ищется решение, и точка х0 лежит внутри этого промежутка, приближенное решение имеет вид табл. 2. Вначале в ней известны х0 и у0, затем отыскиваются остальные табличные данные. Так как правила определения «верхних» и «нижних» (относительно х0 и у0) данных одинаковы, будем искать это решение в виде табл. 3.
Для
построения табл. 3
выбирается шаг
h
и
вычисляются табличные аргументы
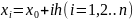 .
Затем
последовательно находятся числа
,
близкие
к значениям точного решения
.
Затем
последовательно находятся числа
,
близкие
к значениям точного решения
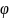 в
точках
:
в
точках
:
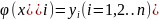
Точность приближенных равенств (5.6) зависит от способа вычисления и от шага таблицы h. Чем меньше шаг, тем выше должна быть точность таблицы. Заданное значение у0 считается точным числом. Погрешности появляются при вычислении у1 , а далее обычно происходит их накопление.
Табл.
3
является
приближением к решению
φ.
Если
на плоскости хОу
построить
точки таблицы (х0,
у0),...,(хn,
уn)
и
соединить их отрезками, получится
так называемая ломаная
Эйлера (рис.
10).
Она будет приближением интегральной
кривой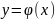 .
.
Теорема.
Если
все частные производные функции
f
до
k-го
(k≥1)
порядка
непрерывны в прямоугольной области
D,
то всякое решение
 уравнения
,
график
которого проходит через внутреннюю
точку (х0,
у0)
этой области, имеет производную
(k+1)-го
порядка,
непрерывную в некоторой окрестности
x0.
уравнения
,
график
которого проходит через внутреннюю
точку (х0,
у0)
этой области, имеет производную
(k+1)-го
порядка,
непрерывную в некоторой окрестности
x0.