Порядок выполнения работы

1 . На координатной плоскости построим график по точкам таблицы (p_i) и убеди­мся, что они располагаются вблизи некоторой квадратной параболы.

Рис.8

Будем искать квадратичную функцию вида

2. Напишем в общем виде систему уравнений для определения коэффициентов многочлена и выражения для коэффициен­тов системы.

3. Составим программу вычисления коэффициентов и решения системы по правилу Крамера.

Текст программы:

const n=6;

type

TArrayXY = array[1..2,1..n] of real;

TArray = array[1..n] of real;

var

SumX,SumY,SumX2,SumXY,SumX3,SumX4,SumX2Y: real;

OPR:real;

c,b,a:real;

i:integer;

const

ArrayXY:TArrayXY=((1.2,1.4,1.5,1.6,1.8,2.1),

(0.9,3.3,4.1,3.9,2.8,1.1));

begin

for i:=1 to n do

begin

SumX:=SumX+ArrayXY[1,i];

SumY:=SumY+ArrayXY[2,i];

SumXY:=SumXY+ArrayXY[1,i]*ArrayXY[2,i];

SumX2:=SumX2+sqr(ArrayXY[1,i]);

SumX3:=SumX3+ArrayXY[1,i]*ArrayXY[1,i]*ArrayXY[1,i];

SumX4:=SumX4+sqr(ArrayXY[1,i])*sqr(ArrayXY[1,i]);

SumX2Y:=SumX2Y+sqr(ArrayXY[1,i])*ArrayXY[2,i];

end;

OPR:=n*SumX2*SumX4+SumX*SumX3*SumX2+SumX2*SumX*SumX3-SumX2*SumX2*SumX2-n*SumX3*SumX3-SumX*SumX*SumX4;

c:=(SumY*SumX2*SumX4+SumX*SumX2Y*SumX3+

SumX2*SumXY*SumX3- SumX2*SumX2*SumX2Y-SumY*SumX3*SumX3-SumX*SumXY*SumX4)/OPR;

b:=(n*SumXY*SumX4+SumY*SumX3*SumX2+SumX2*SumX*SumX2Y-SumX2*SumX2*SumXY-n*SumX3*SumX2Y-SumY*SumX*SumX4)/OPR;

a:=(n*SumX2*SumX2Y+SumX*SumXY*SumX2+SumY*SumX*SumX3-SumY*SumX2*SumX2-n*SumXY*SumX3-SumX*SumX*SumX2Y)/OPR;

writeln('kvadrati4naya funkciya');

writeln('a=',a:8:2);

writeln('b=',b:8:2);

writeln('c=',c:8:2);

end.

Результат, выведенный на экран:

kvadrati4naya funkciya

a= -14.09

b= 46.14

c= -33.89

4. Найдите (округлив коэффициенты до двух цифр в дроб­ной части) и постройте ее график на той же координатной плоско­сти, где отмечены точки таблицы.

Из предыдущего пункта следует, что

График показан на рис.8 как y(x).

5. Найдите все уклонения и среднеквадратичное уклонение мно­гочлена от табличной функции.

Уклонения

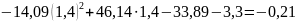
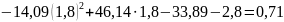
Среднеквадратичное уклонение по всей таблице

8. Приближенное вычисление определенных интегралов Необходимые сведения из теории

8.1. Численный метод приближенного вычисления определенных интегралов

Численные методы позволяют обходиться без аналитических построений. Приближение к интегралу отыскивается по числово­му выражению на основе значений подынтегральной функции в ко­нечном множестве точек из отрезка интегрирования. Такой способ вычислений часто называется механической квадратурой, соответ­ствующие приближенные формулы называют формулами численного интегрирования или квадратурными формулами, а используе­мые при этом аргументы функции — узлами квадратуры.

Общая схема вычислений: берут число , отрезок , разбивают на n равных частей одинаковой длины 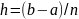(шаг разбиения), из каждой части выбирают узлы x_i , вычисляют а за­тем эти данные подставляют в правую часть квадратурной форму­лы вида

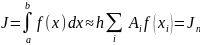
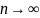Числовые коэффициенты определяют при выводе каждой кон­кретной формулы. Суммы состоят из или слагаемых. Оста­точный член этих формул таков, что при . Это означает, что чем меньше шаг разбиения, тем квадратурная фор­мула точнее, и, следовательно, достаточно мелким разбиением от­резка интегрирования можно обеспечить сколь угодную малость погрешности квадратурных формул.