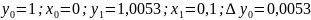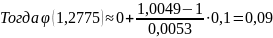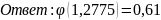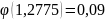- •Міністерство освіти і науки України Національний технічний університет України "Київський політехнічний інститут"
- •Розрахунково-графічна робота з курсу «Обчислювальна математика»
- •Содержание
- •1. Вычисления с учетом погрешностей Необходимые сведения из теории
- •1.1 Абсолютная и относительная погрешности приближенных
- •Чисел и правило их записи.
- •1.2. Верные значащие цифры приближенных чисел.
- •1.3. Нахождение абсолютной погрешности по верным цифрам
- •1.4. Правило округления чисел
- •1.5. Правило записи приближенных чисел
- •1.6. Оценка влияния погрешностей аргументов на значение функции
- •1.7. Оценка погрешностей арифметических действий
- •Задание
- •2. Метод половинного деления Необходимые сведения из теории
- •2.1. Этапы приближенного решения уравнений с одним неизвестным
- •2.2. Отделение корней. Графическое отделение корней
- •2.3. Условия применения метода половинного деления
- •2.4. Алгоритм метода половинного деления
- •2.5. Условие окончания процесса деления при заданной допустимой погрешности
- •Задание
- •3. Комбинированный метод хорд и касательных
- •3.5. Условие окончания процесса вычислений при заданной допустимой погрешности
- •Задание
- •4. Уточнение корней уравнений методом простой итерации Необходимые сведения из теории
- •4.1. Методы отделения корней уравнений
- •4.2. Алгоритм построения итерационной последовательности, порождаемой уравнением )
- •4.3. Достаточное условие сходимости итерационной последовательности
- •4.4. Оценка погрешности n-го приближения к корню
- •4.5. Условие окончания итерационного процесса при заданной допустимой погрешности
- •Задание
- •5. Метод простой итерации приближенного решения систем линейных алгебраических уравнений Необходимые сведения из теории
- •5.1. Способы определения расстояния в пространстве Rn
- •5.2. Абсолютная погрешность числового вектора и его координат
- •5.3. Сходимость последовательности векторов в Rn
- •5.4. Приведенная система уравнений. Cпособы преобразования систем к приведенному виду
- •5.5. Построение итерационной последовательности
- •6. Интерполирование математических таблиц Необходимые сведения из теории
- •6.1. Табличная функция
- •6.2. Задача интерполирования табличной функции
- •6.3. Теорема о единственности задачи полиномиального интерполирования
- •6.4. Конечные разности таблиц
- •6.5. Первый и второй интерполяционные многочлены Ньютона. Оценка погрешностей интерполяционных формул Ньютона
- •6.6. Формула линейного интерполирования и способы оценки ее погрешности
- •6.7. Обратное линейное интерполирование
- •Задание
- •Квадратичное приближение табличных функций по методу наименьших квадратов Необходимые сведения из теории
- •Задача аналитического приближения табличных функций
- •Задача приближения по методу наименьших квадратов
- •7.3. Алгоритм построения наилучшего многочлена по данному методу
- •7.4. Уклонения, среднеквадратичное уклонение
- •Задание
- •Задание по вариантам
- •Порядок выполнения работы
- •8. Приближенное вычисление определенных интегралов Необходимые сведения из теории
- •8.1. Численный метод приближенного вычисления определенных интегралов
- •8.2. Квадратурные формулы трапеций и Симпсона
- •8.3. Строгая оценка погрешностей этих формул
- •8.4. Оценка погрешностей методом двойного пересчета
- •8.5. Определение шага разбиения отрезка интегрирования, при котором квадратурная формула обеспечивает заданную точность
- •8.6. Вопросы оценки точности приближенного интеграла с учетом вычислительных погрешностей
- •Задание
- •Численное решение обыкновенных дифференциальных уравнений методом эйлера-коши Необходимые сведения из теории
- •Общее и частное решения обыкновенного дифференциального уравнения 1-го порядка. Интегральные кривые
- •Задача Коши. Теорема Пикара
- •Геометрический смысл правой части дифференциального уравнения, разрешенного относительно производной
- •Понятие численного решения. Ломаная Эйлера
- •Метод Эйлера- Коши, его геометрический смысл
- •Оценка погрешности численного решения методом двойного пересчета
- •Задание
- •Порядок выполнения работы
- •Использованная литература:
6.6. Формула линейного интерполирования и способы оценки ее погрешности
Пусть
имеется таблица значений функции f
с постоянным шагом h
>
0 и требуется по табличным данным найти
f(x)
при
х,
не
совпадающим с табличными аргументами.
Для этого обозначим через
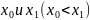 два
соседних табличных аргумента, между
которыми находится х,
через
у0,
у1
—
соответствующие табличные значения, и
из первой интерполяционной формулы
Ньютона при
n
=
1 получим формулу
линейного интерполирования
два
соседних табличных аргумента, между
которыми находится х,
через
у0,
у1
—
соответствующие табличные значения, и
из первой интерполяционной формулы
Ньютона при
n
=
1 получим формулу
линейного интерполирования
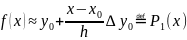
Слагаемое
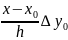 называется
поправкой
к
значению
,
соответствующей
отклонению х
от
.
называется
поправкой
к
значению
,
соответствующей
отклонению х
от
.
Оценочная функция:
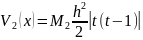
Оценка погрешности:
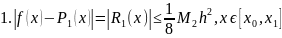
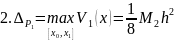

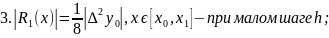
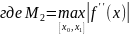
6.7. Обратное линейное интерполирование
Дано
какое-то значение у функции f,
не равное табличным значениям
и необходимо найти соответствующий
аргумент
,
обозначим его как
 Если f
монотонна в области вычисления, то
обратная
для нее функция
там существует, причем она табличная.
Если f
монотонна в области вычисления, то
обратная
для нее функция
там существует, причем она табличная.
Формула обратного линейного интерполирования
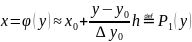
Для вычислений с ее помощью при заданном у выбираются два соседних табличных значения функции f, между которыми находится у, и предыдущее значение принимается за , а последующее — за .
Остаточный член данной формулы выглядит следующим образом:
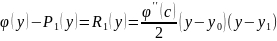
где
с — некоторое число между
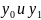 .
Следовательно,
.
Следовательно,
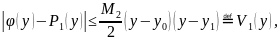
где
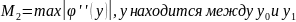
Общая оценка погрешности формулы для всех у, находящихся между , обеспечивается неравенством
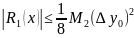
Задание
Дана
таблица значений функции
 с
верными цифрами:
с
верными цифрами:
x |
|
X |
|
X |
|
X |
|
X |
|
0 |
1 |
0,4 |
1,1024 |
0,8 |
1,5082 |
1,2 |
2,3881 |
1,6 |
3,9536 |
0,1 |
1,0053 |
0,5 |
1,1693 |
0,9 |
1,6763 |
1,3 |
2,7057 |
1,7 |
4,4823 |
0,2 |
1,0227 |
0,6 |
1,2575 |
1,0 |
1,8768 |
1,4 |
3,0696 |
1,8 |
5,0758 |
0,3 |
1,0543 |
0,7 |
1,3695 |
1,1 |
2,1130 |
1,5 |
3,4842 |
1,9 |
5,7396 |
Вариант |
а |
b |
с |
d |
10 |
0,96 |
0,92 |
1,2775 |
1,0049 |
Все исходные данные a, b, c, d считаются точными числами.
1. Вычислим приближенное значение с помощью первого интерполяционного многочлена Ньютона второй степени, определим его абсолютную погрешность и верные значащие цифры.
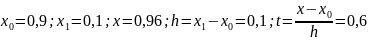
Составим таблицу конечных разностей:
x |
y |
Δy |
Δ2y |
Δ3y |
Δ4y |
0 |
1 |
0,0053 |
0,0121 |
0,0021 |
0,0002 |
0,1 |
1,0053 |
0,0174 |
0,0142 |
0,0023 |
0 |
0,2 |
1,0227 |
0,0316 |
0,0165 |
0,0023 |
0,0002 |
0,3 |
1,0543 |
0,0481 |
0,0188 |
0,0025 |
0 |
0,4 |
1,1024 |
0,0669 |
0,0213 |
0,0025 |
0,0004 |
0,5 |
1,1693 |
0,0882 |
0,0238 |
0,0029 |
-0,0002 |
0,6 |
1,2575 |
0,112 |
0,0267 |
0,0027 |
0,0003 |
0,7 |
1,3695 |
0,1387 |
0,0294 |
0,003 |
0,0003 |
0,8 |
1,5082 |
0,1681 |
0,0324 |
0,0033 |
-0,0001 |
0,9 |
1,6763 |
0,2005 |
0,0357 |
0,0032 |
0,0004 |
1 |
1,8768 |
0,2362 |
0,0389 |
0,0036 |
0,0002 |
1,1 |
2,113 |
0,2751 |
0,0425 |
0,0038 |
0,0006 |
1,2 |
2,3881 |
0,3176 |
0,0463 |
0,0044 |
-0,0003 |
1,3 |
2,7057 |
0,3639 |
0,0507 |
0,0041 |
0,0004 |
1,4 |
3,0696 |
0,4146 |
0,0548 |
0,0045 |
0,001 |
1,5 |
3,4842 |
0,4694 |
0,0593 |
0,0055 |
0 |
1,6 |
3,9536 |
0,5287 |
0,0648 |
0,0055 |
|
1,7 |
4,4823 |
0,5935 |
0,0703 |
|
|
1,8 |
5,0758 |
0,6638 |
|
|
|
1,9 |
5,7396 |
|
|
|
|
Табл. 3 |
|||||
Поскольку вторые разности таблицы практически постоянны, хорошее приближение должен дать многочлен второй степени. Используя данные девятой строки табл.3, на отрезке [0,9; 1,0] будем иметь интерполяционную формулу
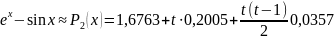
Оценим
погрешность этой формулы в точке
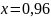 .
Поскольку
.
Поскольку
 для всех
для всех
 ,
примем
,
примем
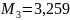 .
Учитывая значение t
=
0,6 , находим
.
Учитывая значение t
=
0,6 , находим

Таким
образом, при
погрешность интерполяции меньше
погрешности таблицы
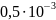 ,
поэтому точность результата определится
точностью табличных данных. Чтобы узнать
степень влияния этих данных, сначала
вычислим
,
поэтому точность результата определится
точностью табличных данных. Чтобы узнать
степень влияния этих данных, сначала
вычислим
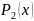 :
:

а
затем найдем оценку
υ
точности
приближения
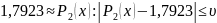 .
Для этого применим правила учета
погрешностей арифметических действий,
имея в виду, что число
.
Для этого применим правила учета
погрешностей арифметических действий,
имея в виду, что число
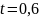 здесь точное. Абсолютные погрешности
табличных данных определим по верным
цифрам значений уi
:
здесь точное. Абсолютные погрешности
табличных данных определим по верным
цифрам значений уi
:
у чисел уi они равны 0,0005, у разностей Δyi — 0,001, у Δ2yi — 0,002. Тогда
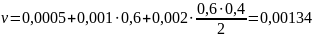
Полученная
оценка
ν
действительно
является основной в суммарной оценке
погрешности приближения 1,7923 к
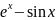 :
:

Теоретически
число 1,7923 имеет только две верные
значащие цифры после запятой. Для
сравнения приведем искомое значение
функции с пятью верными значащими
цифрами, рассчитанное на калькуляторе: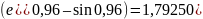 .
Расстояние
.
Расстояние
 показывает,
что при учете вычислительной
погрешности получена завышенная ее
оценка (в основном за счет завышения
оценок погрешностей значений уi
и
конечных разностей по сравнению с
их реальными погрешностями). На самом
деле верными являются три цифры после
запятой.
показывает,
что при учете вычислительной
погрешности получена завышенная ее
оценка (в основном за счет завышения
оценок погрешностей значений уi
и
конечных разностей по сравнению с
их реальными погрешностями). На самом
деле верными являются три цифры после
запятой.
Ответ:
 .
.
2.
Линейным интерполированием найдите
значения функции f
для аргументов
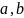 и определите их верные значащие цифры
с помощью таблицы конечных разностей.
и определите их верные значащие цифры
с помощью таблицы конечных разностей.
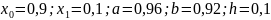
Поскольку
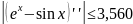 для всех
,
примем
для всех
,
примем
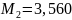 .
Сначала
применим общие для всех
неравенства оценки
погрешностей:
.
Сначала
применим общие для всех
неравенства оценки
погрешностей:
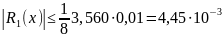
Так как Δ2y=0,0357 (из табл. 3),
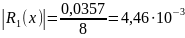
Обе оценки почти одинаковы и показывают, что не только числам а и b, но и всем другим приближениям к функции, для всех , формула обеспечивает по крайней мере две верные значащие цифры после десятичной запятой.
Из оценочной функции
1)
для
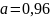 :
:
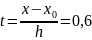

2)
для
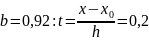
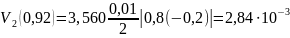
Следовательно, в обоих случаях формула даст нам две верные цифры. Найдем искомые приближения:
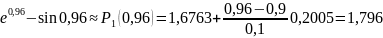
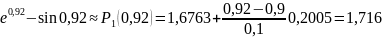
Для
оценки точности вычислений определяем
абсолютные погрешности чисел у0
=
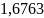 и Δу0
=
0,042 по известным верным цифрам табличных
значений
и Δу0
=
0,042 по известным верным цифрам табличных
значений
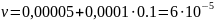
Точность значения Р1(1,11) оценится числом ν = 0,0005 + 0,1 · 0,001 = 0,0006.
Добавляем 0,00006 к подсчитанной ранее оценке
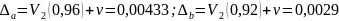
Значит, у a и b будет две верные цифры после запятой.
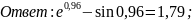
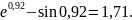
3. Вычислим значения обратной для d функции φ для аргументов с, d по формуле обратного линейного интерполирования и запишите ответы с двумя цифрами после десятичной запятой.
1)
Для
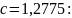
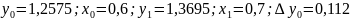
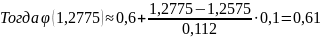
2)
Для
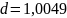 :
: