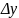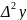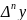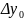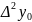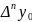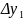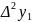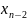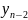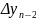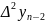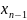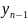- •Міністерство освіти і науки України Національний технічний університет України "Київський політехнічний інститут"
- •Розрахунково-графічна робота з курсу «Обчислювальна математика»
- •Содержание
- •1. Вычисления с учетом погрешностей Необходимые сведения из теории
- •1.1 Абсолютная и относительная погрешности приближенных
- •Чисел и правило их записи.
- •1.2. Верные значащие цифры приближенных чисел.
- •1.3. Нахождение абсолютной погрешности по верным цифрам
- •1.4. Правило округления чисел
- •1.5. Правило записи приближенных чисел
- •1.6. Оценка влияния погрешностей аргументов на значение функции
- •1.7. Оценка погрешностей арифметических действий
- •Задание
- •2. Метод половинного деления Необходимые сведения из теории
- •2.1. Этапы приближенного решения уравнений с одним неизвестным
- •2.2. Отделение корней. Графическое отделение корней
- •2.3. Условия применения метода половинного деления
- •2.4. Алгоритм метода половинного деления
- •2.5. Условие окончания процесса деления при заданной допустимой погрешности
- •Задание
- •3. Комбинированный метод хорд и касательных
- •3.5. Условие окончания процесса вычислений при заданной допустимой погрешности
- •Задание
- •4. Уточнение корней уравнений методом простой итерации Необходимые сведения из теории
- •4.1. Методы отделения корней уравнений
- •4.2. Алгоритм построения итерационной последовательности, порождаемой уравнением )
- •4.3. Достаточное условие сходимости итерационной последовательности
- •4.4. Оценка погрешности n-го приближения к корню
- •4.5. Условие окончания итерационного процесса при заданной допустимой погрешности
- •Задание
- •5. Метод простой итерации приближенного решения систем линейных алгебраических уравнений Необходимые сведения из теории
- •5.1. Способы определения расстояния в пространстве Rn
- •5.2. Абсолютная погрешность числового вектора и его координат
- •5.3. Сходимость последовательности векторов в Rn
- •5.4. Приведенная система уравнений. Cпособы преобразования систем к приведенному виду
- •5.5. Построение итерационной последовательности
- •6. Интерполирование математических таблиц Необходимые сведения из теории
- •6.1. Табличная функция
- •6.2. Задача интерполирования табличной функции
- •6.3. Теорема о единственности задачи полиномиального интерполирования
- •6.4. Конечные разности таблиц
- •6.5. Первый и второй интерполяционные многочлены Ньютона. Оценка погрешностей интерполяционных формул Ньютона
- •6.6. Формула линейного интерполирования и способы оценки ее погрешности
- •6.7. Обратное линейное интерполирование
- •Задание
- •Квадратичное приближение табличных функций по методу наименьших квадратов Необходимые сведения из теории
- •Задача аналитического приближения табличных функций
- •Задача приближения по методу наименьших квадратов
- •7.3. Алгоритм построения наилучшего многочлена по данному методу
- •7.4. Уклонения, среднеквадратичное уклонение
- •Задание
- •Задание по вариантам
- •Порядок выполнения работы
- •8. Приближенное вычисление определенных интегралов Необходимые сведения из теории
- •8.1. Численный метод приближенного вычисления определенных интегралов
- •8.2. Квадратурные формулы трапеций и Симпсона
- •8.3. Строгая оценка погрешностей этих формул
- •8.4. Оценка погрешностей методом двойного пересчета
- •8.5. Определение шага разбиения отрезка интегрирования, при котором квадратурная формула обеспечивает заданную точность
- •8.6. Вопросы оценки точности приближенного интеграла с учетом вычислительных погрешностей
- •Задание
- •Численное решение обыкновенных дифференциальных уравнений методом эйлера-коши Необходимые сведения из теории
- •Общее и частное решения обыкновенного дифференциального уравнения 1-го порядка. Интегральные кривые
- •Задача Коши. Теорема Пикара
- •Геометрический смысл правой части дифференциального уравнения, разрешенного относительно производной
- •Понятие численного решения. Ломаная Эйлера
- •Метод Эйлера- Коши, его геометрический смысл
- •Оценка погрешности численного решения методом двойного пересчета
- •Задание
- •Порядок выполнения работы
- •Использованная литература:
6.3. Теорема о единственности задачи полиномиального интерполирования
Наиболее часто интерполирующую функцию ищут в виде многочлена (полинома). Тогда интерполирование называют полиномиальным, а соответствующий многочлен — интерполяционным. Задача полиномиального интерполирования всегда имеет решение.
Теорема. Пусть известна табл.1 значений функции f с n+1 аргументом. Тогда существует единственный многочлен
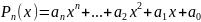
степени п, удовлетворяющий равенствам
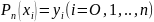 .
.
Таким образом, для любой табличной функции найдется единственный интерполяционный многочлен, степень которого в общем случае па единицу меньше количества узлов интерполирования.
6.4. Конечные разности таблиц
В случае таблиц с равноотстоящими узлами используются величины, называемые конечными разностями. Конечные разности первого порядка — это разности между соседними табличными значениями:
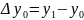
Формула
для конечных
разностей k-го
порядка
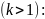
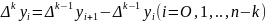
Для
табл. 1 разностью наивысшего порядка
будет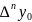 .
.
Можно
определять разности функций в произвольной
точке а;при некотором шаге
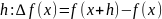 (приращение
функции),
(приращение
функции),
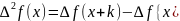 и
т.д.
и
т.д.
Конечные разности удобно располагать в форме таблиц
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Табл.2
|
|||||
По таблице конечных разностей часто удается находить наилучшую степень интерполяционного многочлена. Если разности k-ого порядка на каком-то участке таблицы практически постоянны, то это значит, что здесь табличная функция близка к многочлену k-ой степени.
6.5. Первый и второй интерполяционные многочлены Ньютона. Оценка погрешностей интерполяционных формул Ньютона
Первый интерполяционный многочлен Ньютона:
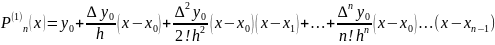
Приближенное
равенство:
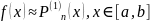 называется
первой
интерполяционной формулой Ньютона.
называется
первой
интерполяционной формулой Ньютона.
На
практике чаще всего используется другая
форма записи многочлена
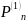 .
Положим
.
Положим
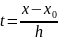 или
или
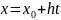 .
Тогда
.
Тогда
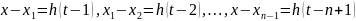 .
С
учетом полученных соотношений многочлен
.
С
учетом полученных соотношений многочлен
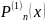 примет вид
примет вид
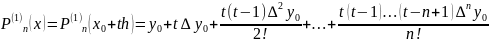
Выражение для остаточного члена
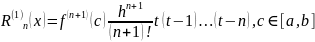
и оценочной функции
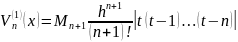
где
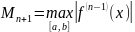 .
.
С
помощью первой интерполяционной формулы
Ньютона обычно вычисляют значения
функции f
для x,
близких
к х0,
т.е.
находящихся в начале
таблицы.
Это обстоятельство следует учитывать
при выборе узлов для построения
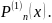
Второй интерполяционный многочлен Ньютона
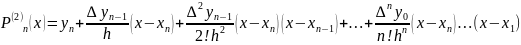
Приближенное
равенство:
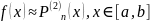 называется
второй
интерполяционной формулой Ньютона.
называется
второй
интерполяционной формулой Ньютона.
Положим
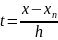 или
или
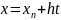 :
:
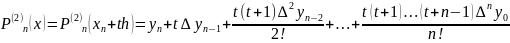
Выражение для остаточного члена
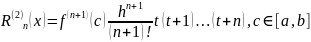
и оценочной функции
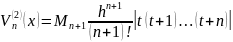
где
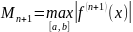 .
.