Міністерство освіти і науки України Національний технічний університет України "Київський політехнічний інститут"

Факультет електроніки

Кафедра акустики та акустоелектроніки

Розрахунково-графічна робота з курсу «Обчислювальна математика»

Перевірив: К.т.н., ст.викладач Богданова Н.В.

Виконала: Студентка групи ДГ82 Михеєва Анастасія Миколаївна

КИЕВ – 2009

Содержание

1. Вычисления с учетом погрешностей……………………………………………3

2. Метод половинного деления…………………………………………………..10

3. Комбинированный метод хорд и касательных……………………………….16

4. Уточнение корней уравнений методом простой итерации…………………21

5. Метод простой итерации приближенного решения систем линейных алгебраических уравнений……………………………………………………….27

6. Интерполирование математических таблиц…………………………………35

7. Квадратичное приближение табличных функций по методу наименьших квадратов……………………………………………………………………………45

8. Приближенное вычисление определенных интегралов……………………..53

9. Численное решение обыкновенных дифференциальных уравнений методом Эйлера-Коши…………………………………………………………….………..59

Использованная литература………………………………………..…………….68

1. Вычисления с учетом погрешностей Необходимые сведения из теории

1.1 Абсолютная и относительная погрешности приближенных

Чи­сел и правило их записи.

Пусть А — точное значение некоторой числовой, векторной или функциональной величины, a — известное приближение к нему (т. е. приближенное значение для А). Обозначаем: А ≈ а или а≈ А. В зависимости от типа величины принято называть А точным числом (вектором, функцией), а его приближение а — приближен­ным числом (вектором, функцией). Например, в соотношениях π ≈ 3,14, π ≈ 3,142 число π является точным, а числа 3,14, 3,142 — приближенными (приближениями к π).

1. Разность А - α (или а - А) между точным и приближенным значениями величины называется погрешностью значения a.

2. Любое неотрицательное число Δ_а , удов­летворяющее неравенству

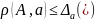
называется абсолютной погрешностью приближенного значения a (относительно р).

Число Δ_α устанавли­вает «верхний предел» для значений расстояния; с его помо­щью можно найти границы, т.е. «пределы от ... и до ...», в которых находится неизвестное точное значение А.

Как число Δ„, так и само неравенство (*) называют также оцен­кой погрешности (точности) значения о или приближенного равен­ства А ≈ а. Чтобы отличать эту оценку от приближенных оценок вида ρ(А, а) ≈ А, иногда ее называют строгой оценкой.

Если а — приближенное число, то неравенство (*) примет вид

│А – а│≤ Δ_α

Абсолютная погрешность определяется неоднозначно. На практике стараются в качестве Δ_α выбрать возможно меньшее при данных обстоятельствах число, удовлетворяющее (*).

Если точное значение А известно, можно принять 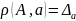. Когда α является точным значением, т.е. а = А, будет 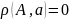. Тогда и Δ_α = 0.

Абсолютная погрешность даст ценную информацию о неизвест­ном точном значении А: оно находится от известного приближе­ния а на расстоянии, не большем чем Δ_а. В случае числовых вели­чин имеем

│А – а│≤ Δ_α <=> а – Δ_а ≤ А ≤ а + Δ_а.

Следовательно, найдя приближенное значение а и его абсолют­ную погрешность Δ_а, узнаем, что точное значение А располагается на отрезке [а - Δ_а; а + Δ_α].

3. Если известна абсолютная погрешность Δ_α приближенного значения а, то а называют приближением к Ас точ­ностью до Δ_а.

Когда говорят, что надо получить результат с заданной точностью ε > 0, это означает, что абсолютная погрешность его дол­жна быть не больше ε.

4. Все цифры десятичной записи числа, на­чиная с первой ненулевой слева, называются значащими цифрами этого числа. Нули в конце числа всегда считаются значащими, иначе их не пишут. Так, число 0,05020 содержит четыре значащие цифры: 5,0,2 и 0.

Абсолютную погрешность не следует записывать с большим ко­личеством значащих цифр. Основной информацией, содержащейся в ней, являются значение первой ненулевой цифры и десятичный разряд, в котором эта цифра расположена.

Правило. В записи абсолютной погрешности обычно оставля­ют только одну или две значащие цифры. Для сохранения условия (1) округление при этом всегда производится с избытком.

Как и всякое действительное число, абсолютную погрешность мож­но записывать в так называемой плавающей форме (с плавающей де­сятичной запятой)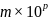 . Здесь т называется мантиссой числа, а р — его порядком.

Для оценки качества измерений или вычислений вводится поня­тие относительной погрешности.

5. Относительной погрешностью (часто называют предельной относительной погрешностью) прибли­женного числа а (а≠0) назывют неотрицательное число

Формула (2) связывает абсолютную и относительную погреш­ности чисел. Из нее, в частности, следует важное соотношение:

Δ_а = |а|δ_а.

Из-за неоднозначности абсолютной погрешности относительная погрешность приближенного числа также не единственна. Как и абсолютную погрешность, относительную погрешность записывают с одной-двумя значащими цифрами и округляют при необходимости с избытком. Она является безразмерной величиной и потому часто выражается в процентах:

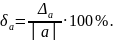
При фиксированном Δ_α относительная погрешность тем меньше, чем больше абсолютная величина приближенного чис­ла.

Правило записи приближенных чисел. В промежу­точных результатах вычислений обычно сохраняются одна-две со­мнительные цифры, а окончательные результаты округляют с со­хранением не более одной сомнительной цифры.