7. Двойная логарифмическая модель

Вычислим логарифмы столбцом х и y и по новым полученным столбцам с помощью Excel найдем неизвестные величины.

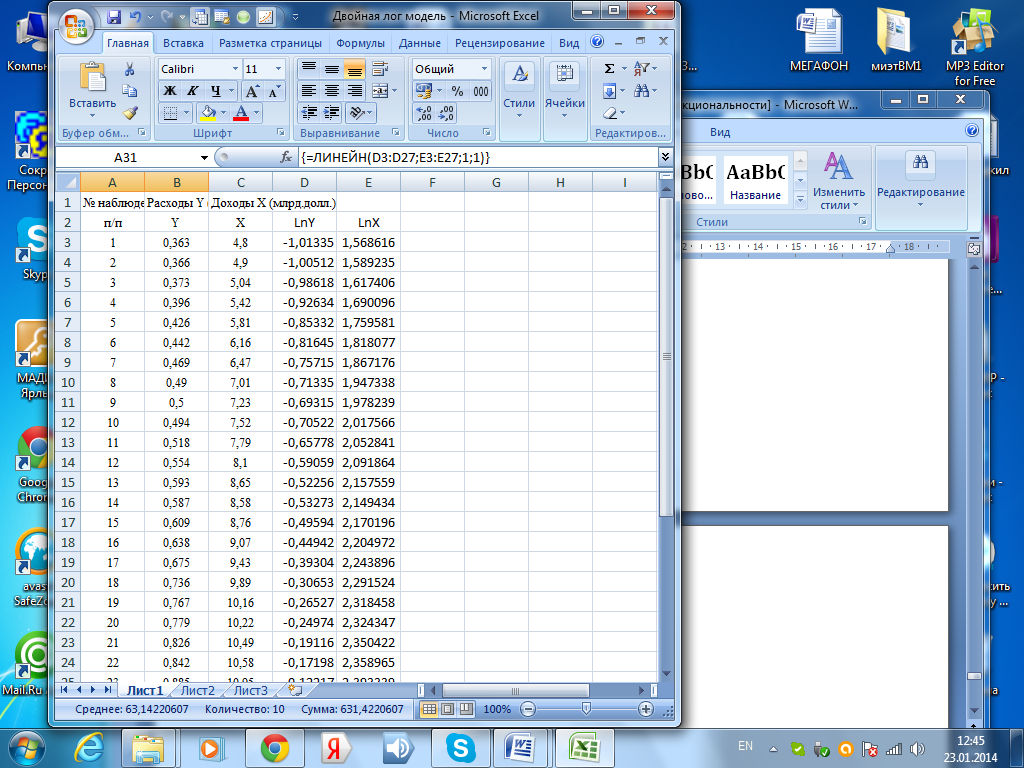
Полученные результаты трактуем соответственно ниже приведенной таблице.

Значение коэффициента b	Значение коэффициента a
Среднеквадратическое отклонение b	Среднеквадратическое отклонение a
Коэффициент детерминации R2	Среднеквадратическое отклонение y
F – статистика	Число степеней свободы
Регрессионная сумма квадратов	Остаточная сумма квадратов

Также с помощью РЕГРЕССИЯ получаем искомые параметры:

Объединив результаты построения парных регрессии в одной таблице 4, выберем наилучшую модель.

Таблица 4

Уравнение регрессии	Коэффициент детерминации	- статистика критерий Фишера	Средняя ошибка аппроксимации ,%
Линейная модель = - 0,08531 + 0,084061*X	0,959275	541,7701176	3,2676252
	0,934777948	329,6415	5,233239
	0,988921604	2053,11286	0,8889002
	0,829294287	111,734799	13,6969594
Линейно логарифмическая	0,904306225	217,3500114	7.6782067
Показательная модель	0,991027	2054,213	6,76
Двойная лог. модель	0,963478	606,754	5,92

Общий вывод по заданию в целом.

Все уравнения регрессии достаточно хорошо описывают исходные данные. Предпочтение можно отдать показательной модели , для которой значение коэффициента детерминации и F-критериев Фишера наибольшие, а ошибка аппроксимации – средняя.

Следовательно, для построения дальнейших прогнозов и принятия решений лучше применить показательную модель парной регрессии.