3. Использование режимов статистических сравнений для решения статистических задач

З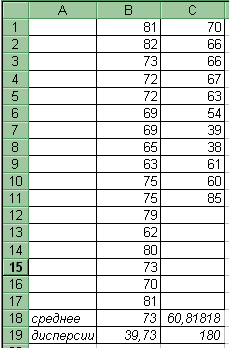 адание 1. Изучается проблема психологических барьеров при обращении в службу знакомств у мужчин и женщин. В эксперименте участвовали 17 мужчин и 11 женщин в возрасте от 17 до 45 лет. Испытуемые должны были отметить на отрезке точку, соответствующую интенсивности внутреннего сопротивления, которое им пришлось преодолеть, чтобы обратиться в службу знакомств. Длина отрезка составляла 100 мм. В таблице приведены показатели интенсивности сопротивления, выраженные в миллиметрах. Предварительным анализом было установлено, что внутреннее сопротивление подчиняется нормальному закону распределения и у мужчин ²_x =39, 73, а у женщин ²_y=68,45. Можно ли утверждать, что среднее внутреннее сопротивление у мужчин совпадает с сопротивлением у женщин? Проверить выдвинутую гипотезу при уровне значимости 0,05.

Решение

1. Сформулируйте гипотезу H₀: а_x = a_y при альтернативной H₁: a_xa_y. На рабочем листе Microcoft Excel оформите таблицу с исходными данными.

2. В ячейках В18 и С18 найдите среднее математическое ожидание, используя формулу =СРЗНАЧ(В1:В17) и =СРЗНАЧ(С1:С11).

3. В ячейки В19 и С19 внесите данные дисперсии.

4. Д 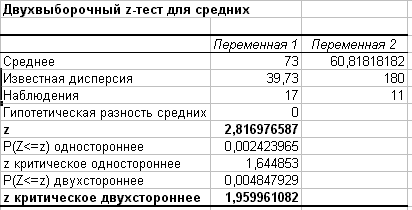алее используйте режим работы «Двухвыборочный - тест для средних», введя соответствующие параметры. Так как расчетное значение параметра больше критического, то нулевую гипотезу отвергаем (2,81>1,95). Считаем, что различие выборочных средних неслучайно. Более того, если рассматривать конкурирующую гипотезу Н₁: а_x > a_y, то критическая область – правосторонняя (1,64; ) и наблюдаемое значение попадает в критическую область, а следовательно нулевую гипотезу отклоняем и принимаем альтернативную. Следовательно, мужчинам приходится преодолевать более сильное внутреннее сопротивление, чем женщинам.

Задание 2. Выборочные данные о расходе сырья при производстве продукции по старой и новой технологиям приведены в таблице, сформированной на рабочем листе Microcoft Excel. При уровне значимости =0,05 требуется проверить гипотезу H₀: а_x = a_y, предположив, что соответствующие генеральные совокупности X и Y имеют нормальные распределения:

1. с одинаковыми дисперсиями;2 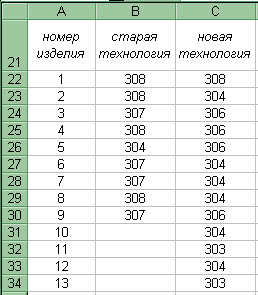) с различными дисперсиями.

Решение.

Д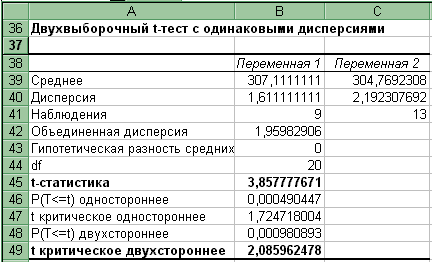 ля проверки предположения 1 используем режим работы «Двухвыборочный t-тест с одинаковыми дисперсиями», а для проверки предположения 2 – «Двухвыборочный t-тест с различными дисперсиями». Рассчитанные показатели для первого предположения представлены в таблице.

Так как расчетное значение критерия t_р=3,86 больше критического t_к=2,09, то нулевую гипотезу H₀: а_x = a_y отвергаем, то есть при переходе на новую технологию происходит изменение среднего расхода сырья на одно изделие.

Расчеты второго показателя незначительно будут отличаться от первого.

Задание 3 (самостоятельно). Используя данные задания 1, и считая, что генеральные дисперсии не известны, перепроверить гипотезу о равенстве средних на уровне значимости 0,05.

Задание 4 (самостоятельно). Используйте данные задания 3 рассчитайте одностороннее и двустороннее Р-значение t-теста по формуле ТТЕСТ. Сравните полученные значения. Есть ли отличия Р-значений полученных по формуле ТТЕСТ и вычисляемых функцией СТЬЮРАСП, используемой в режимах «Двухвыборочный t- тест c одинаковыми дисперсиями» и «Двухвыборочный t- тест c различными дисперсиями» и почему?

З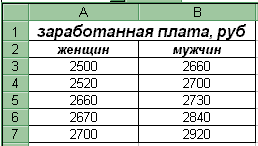 адание 5 (самостоятельно). Имеются следующие данные выборочного обследования размера заработной платы у 5 мужчин и 5 женщин в одном НИИ. На уровне значимости 0,05 проверить, можно ли считать случайным расхождения между средней заработной платой мужчин и женщин.

Сформулируем гипотезу о равенстве дисперсий двух нормальных генеральных совокупностей. Рассмотрим две случайные величины X и Y, каждая из которых подчиняется нормальному закону распределения с дисперсиями ²_x и ²_y. Проверим гипотезу Н₀: ²_x= ²_y на основании альтернативной гипотезы Н₁: ²_x> ²_y. Для оценки ²_x используется

Задание 6. Используя выборочные данные о расходе сырья по старой и новой технологиям задания 2, установите, можно ли при уровне значимости =0,05 считать статистически незначимым различие между оценками s_х²=1,61 и s_y²=2,19, рассчитанными в задаче.

Решение.

Д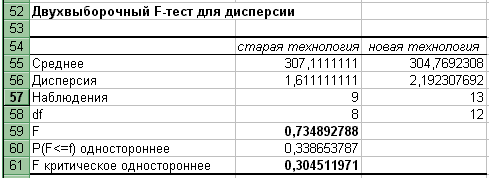 ля проверки гипотезы Н₀: ²_x= ²_y, приняв в качестве альтернативной Н₁: ²_x ²_y, используем режим работы «Двухвыборочный F- тест для дисперсий». Получим следующие показатели.

В отличие от ранее рассмотренных режимов проверки статистических гипотез, в режиме«Двухвыборочный F- тест для дисперсий» рассчитываются только односторонние оценки Р-значения (ячейка 60) и F^кр_лев,(ячейка 61). Это объясняется тем, что в данном режиме в качестве альтернативной гипотезы рассматривается гипотеза Н₁: ²_x< ²_y (или ²_x> ²_y).

Из таблицы видно, что расчетное значение критерия F_р=0,73 не попадает в критическую область (0; 0,30), то гипотезу о равенстве дисперсий расхода сырья по старой и новой технологиям принимаем.

Расчетное значение критерия вычисляется в ячейке В59 по формуле =В56/С56, где в ячейках В56 и С56 рассчитываются оценки дисперсий с помощью функции ДИСП.

Число степеней свободы рассчитывается в ячейках В58 и С58.

Значение левосторонней критической точки определяется в ячейке В61 по формуле =FРАСПОБР(1-0,05;В58;С58).

Задание 7 (самостоятельно). В задании 6 одностороннее Р-значение F- теста рассчитывалось по формуле =FРАСП (В59;В58;С58), которая адекватна формуле ФТЕСТ. Проверьте полученные значения.

80