- •(Тени в аксонометрии. Тени в перспективе)
- •1.Тени в аксонометрии
- •1.1.Тень от точки
- •1.2. Тени геометрических тел
- •1.3.Примеры построения теней архитектурных деталей
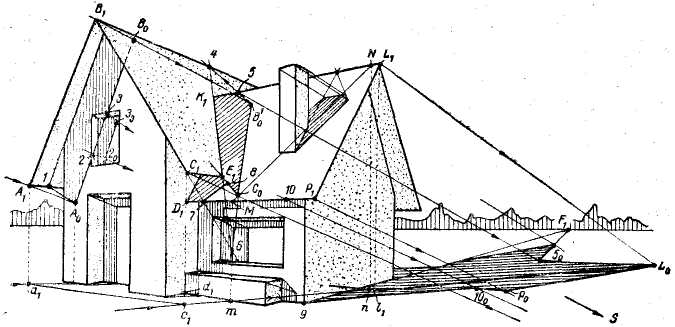
- •2.Тени в перспективе
- •2.1. Тени от точки, от прямой и геометрических тел
- •2.2. Примеры построения теней архитектурных деталей
- •2.3. Построение теней при искусственном источнике света
- •3.Содержание
- •1. Тени в аксонометрии…………………………………………………...……..2
- •1.1.Тень от точки………………………………………………………………....2
- •1.2.Тени геометрических тел……………………………………………….......3
- •4.Список литературы
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ ФИЛИАЛ ФЕДЕРАЛЬНОГО ГОСУДАРСТВЕННОГО БЮДЖЕТНОГО УЧРЕЖДЕНИЯ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«КАМСКАЯ ГОСУДАРСТВЕННАЯ ИНЖЕНЕРНО – ЭКОНОМИЧЕСКАЯ АКАДЕМИЯ»
В Г.ЧИСТОПОЛЕ
ЛЕКЦИИ
по дисциплине:
«Инженерная графика»
(Тени в аксонометрии. Тени в перспективе)
для специальности 270800.62
г. Чистополь
1.Тени в аксонометрии
При построении теней в аксонометрических проекциях направление световых лучей может быть принято любым и задается первичной и одной из вторичных проекций светового луча.
Направление световых лучей выбирается с учетом получения светотеневого рисунка, выявляющего наилучшим образом объемный рельеф и конфигурацию здания или сооружения.
Основные положения, рассмотренные при построении теней в ортогональных проекциях, остаются в силе и при построении теней в аксонометрии.
1.1.Тень от точки
На рис. 1 точка А задана первичной и горизонтальной проекциями. Направление световых лучей также задано первичной проекцией S и горизонтальной проекцией s.
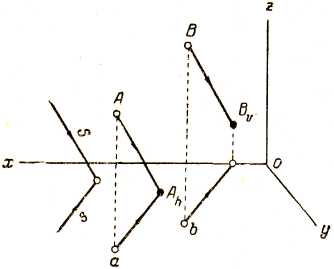
Рис. 1
Для построения падающей тени от точки А проводим через эту точку световой луч принятого направления (через первичную проекцию точки проводим первичную проекцию светового луча, а через горизонтальную проекцию — горизонтальную проекцию светового луча). Точка пересечения светового луча с плоскостью или поверхностью, встретившейся на его пути, и будет являться падающей тенью от данной точки. На рис. 1 тень от точки А падает на горизонтальную плоскость проекций, а тень от точки В — на фронтальную плоскость проекций.
1.2. Тени геометрических тел
При построении теней геометрических тел приходится определять контуры как собственных, так и падающих теней. Так как контур падающей тени строится от контура собственной тени, то в первую очередь следует определять, в общем случае, контур собственной тени.
Контур собственной тени призмы (рис. 2) при заданном направлении световых лучей представляет собой замкнутую ломаную линию ABCDEFA, участками которой являются ребра призмы.
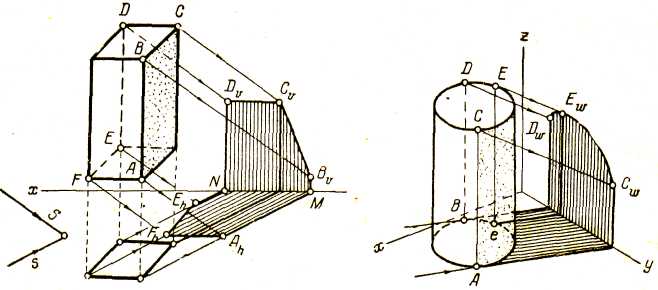
Рис. 2 Рис. 3
От контура собственной тени строится контур AhBvCvDvEhFhAh падающей тени с точками перегиба М и N на оси х. На рис. 3 построены тени цилиндра, стоящего своим основанием на горизонтальной плоскости. Горизонтальные проекции световых лучей, проведенные касательно к основанию цилиндра, определяют точки А и В — основания образующих цилиндра, которые являются линиями раздела света и тени боковой поверхности цилиндра. К контуру собственной тени относится также дуга CED верхнего основания цилиндра. От указанного контура строится контур падающей тени, для чего достаточно определить падающие тени Cw и Dw от точек С и D, а также тени от ряда промежуточных точек дуги CED верхнего основания цилиндра (см. тень E,w).
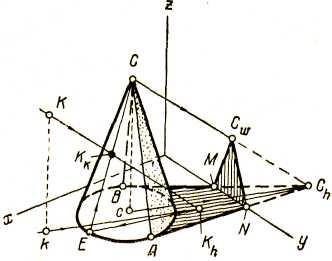 Рис.
4
Рис.
4
При построении теней конуса (рис. 4) в первую очередь строится тень Ch от вершины конуса на плоскость его основания. Проведенные из точки Ch прямые, касательные к основанию конуса, определяют собой контур тени, падающей на горизонтальную плоскость, а также точки А и В, через которые проходят образующие АС и ВС, являющиеся контуром собственной тени конуса.
Тень от конуса в данном случае падает частично и на профильную плоскость проекций, на которой контур тени определяется точками перегиба М и N и реальной тенью Cw от вершины конуса.
На этом же чертеже показано построение падающей тени Kk на поверхность конуса от точки К. Для определения указанной тени находим вначале ложную тень Kh от точки К на горизонтальной плоскости, через которую из точки Ch проводим прямую, и в пересечении ее с основанием конуса отмечаем точку Е.
Прямая ECh является тенью образующей конуса, на которой должна находиться падающая тень Kh от точки К. Проводим из точки Е образующую ЕС. В пересечении ее с первичной проекцией светового луча, проведенной через первичную проекцию точки К, находим искомую тень от точки К на поверхности конуса.