5. Алгоритм решения проблемной задачи.

1. Находим опорный план чисел заполненных клеток должно быть равным n + m – 1

2. Находят потенциалы α_i, β_j соответственно пунктов назначения и отправления.

3. Для каждой свободной клетки определяет число α_ij. Если среди чисел α_ij нет положительных, то решение оптимальное; если они имеются то переходят к новому опорному плану.

4. Среди положительных чисел α_ij выбирают максимальный и строят для свободной клетки цикл пересчета и производят сдвиг по циклу пересчета.

5. Проверяют полученный опорный план на оптимальность, то есть снова повторяют все действия начиная со второго этапа.

4. Список литературы.

2. Заключение.

Для определения оптимального плана транспортной задачи разработано несколько методов. Наиболее часто встречаемые являются метод потенциалов, модифицировано- распределительный метод и метод дифференциальных рент.

Общий принцип определения оптимального плана транспортной задачи методом потенциалов аналогичен принципу решения задачи линейного программирования симплексным методом, а именно : сначала находят опорный план транспортной задачи, а затем его последовательно улучшают до получения оптимального плана. Но наиболее применимый метод – метод потенциалов.

5. Реализация алгоритма задачи.

Рассматриваемый автосервис представляет собой одноканальную систему массового обслуживания с ожиданием без ограничений на длину очереди и время ожидания. Параметры системы: 

• число каналов (число рабочих мест) n=1;

• интенсивность входящего потока 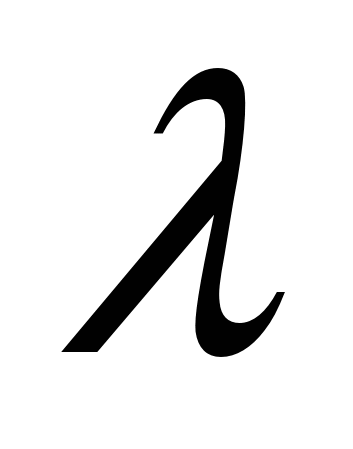 =2 чел./ч.;

• интенсивность потока обслуживания 1-го механика = =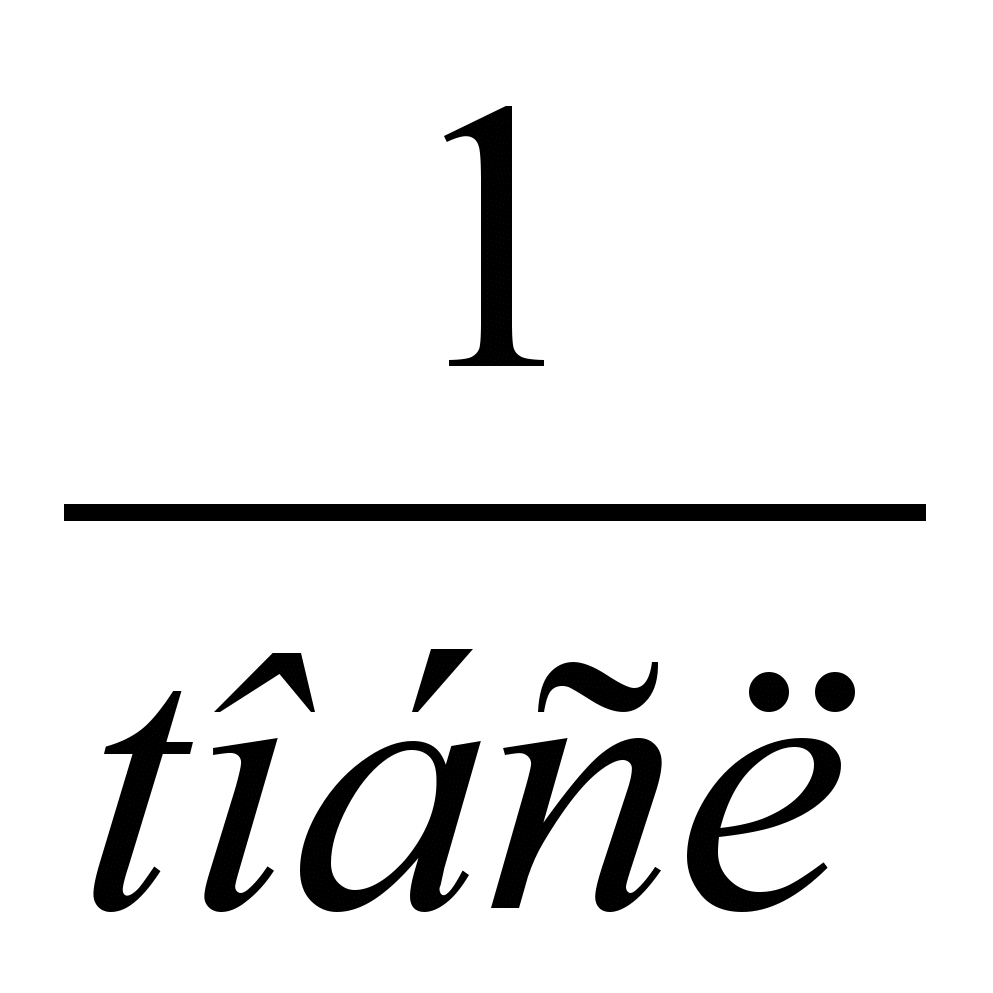3 чел./ч.

2-го механика = =4 чел./ч.

• Издержки компании по ожиданию клиентами своей очереди C_ож=15 ден.ед.

• Издержки компании по найму на работу1-го механика C_экспл=7 ден.ед.

2-го механика C_экспл=10 ден.ед.

1. Рассчитываем интенсивность нагрузки:

1-го механика  2-го механика 

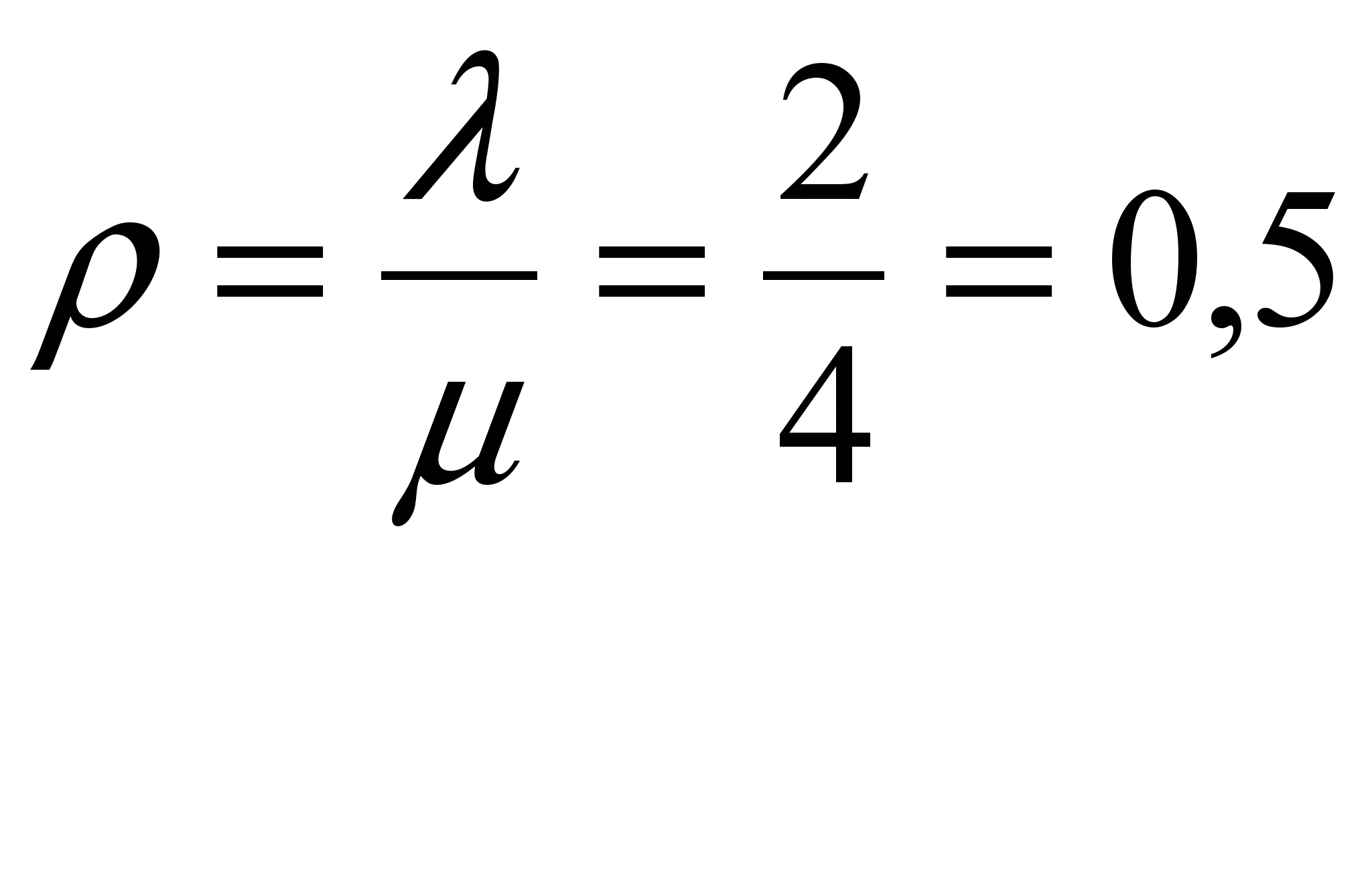
2. Рассчитываем нагрузку на один канал:

1-го механика  2-го механика 

3. 0,667 и 0,5 < 1, то предельный режим функционирования системы существует, и мы можем определить основные характеристики эффективности СМО в данном режиме: 

   1. Определяем вероятность того, что система обслуживания окажется незанятой при условии найма одного или второго работника:

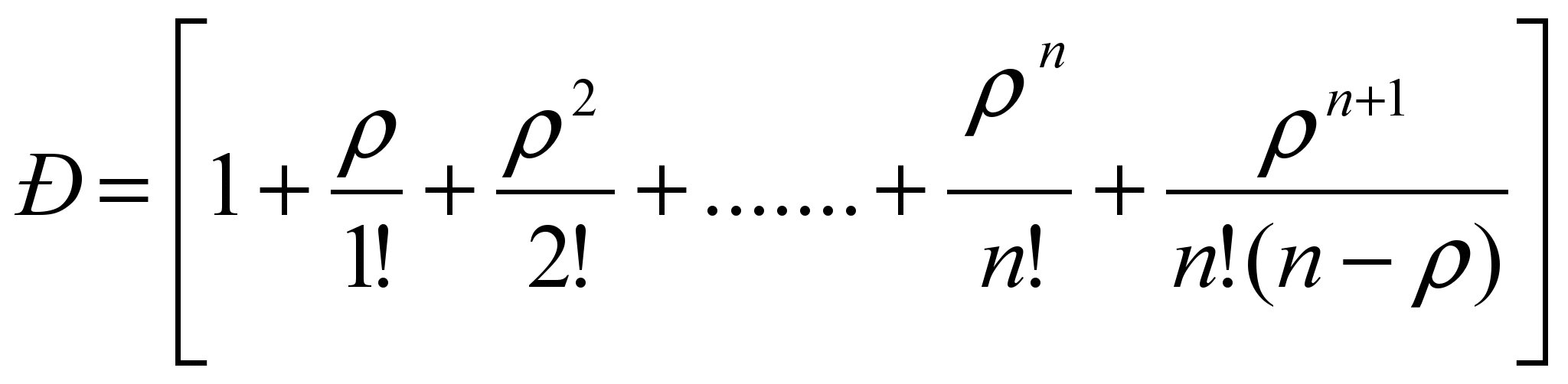=  Р₁= =3,006^-1= Р₂= =2^-1=

2. Находим среднее число занятых каналов:

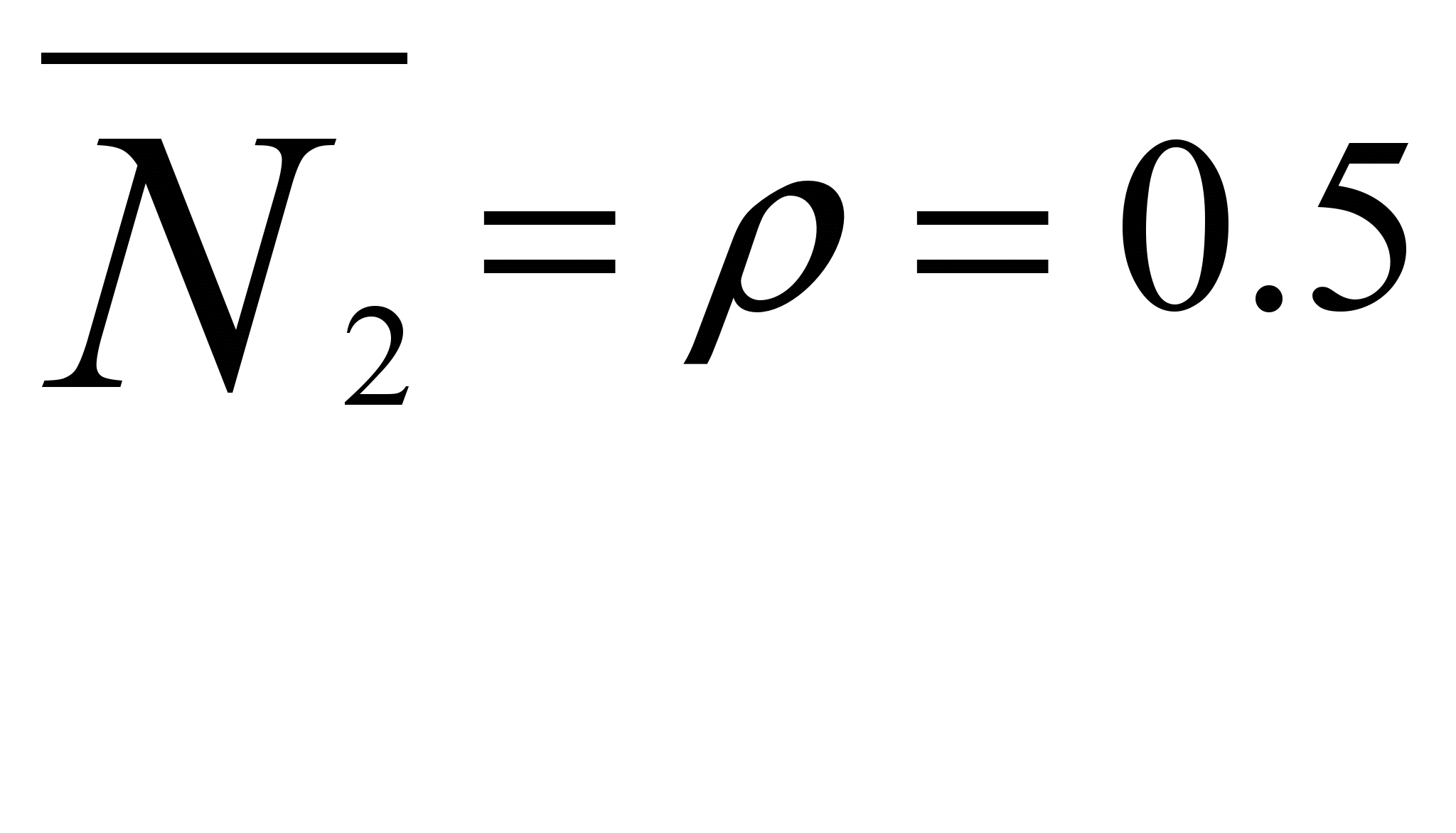
3. Находим среднюю длину очереди:

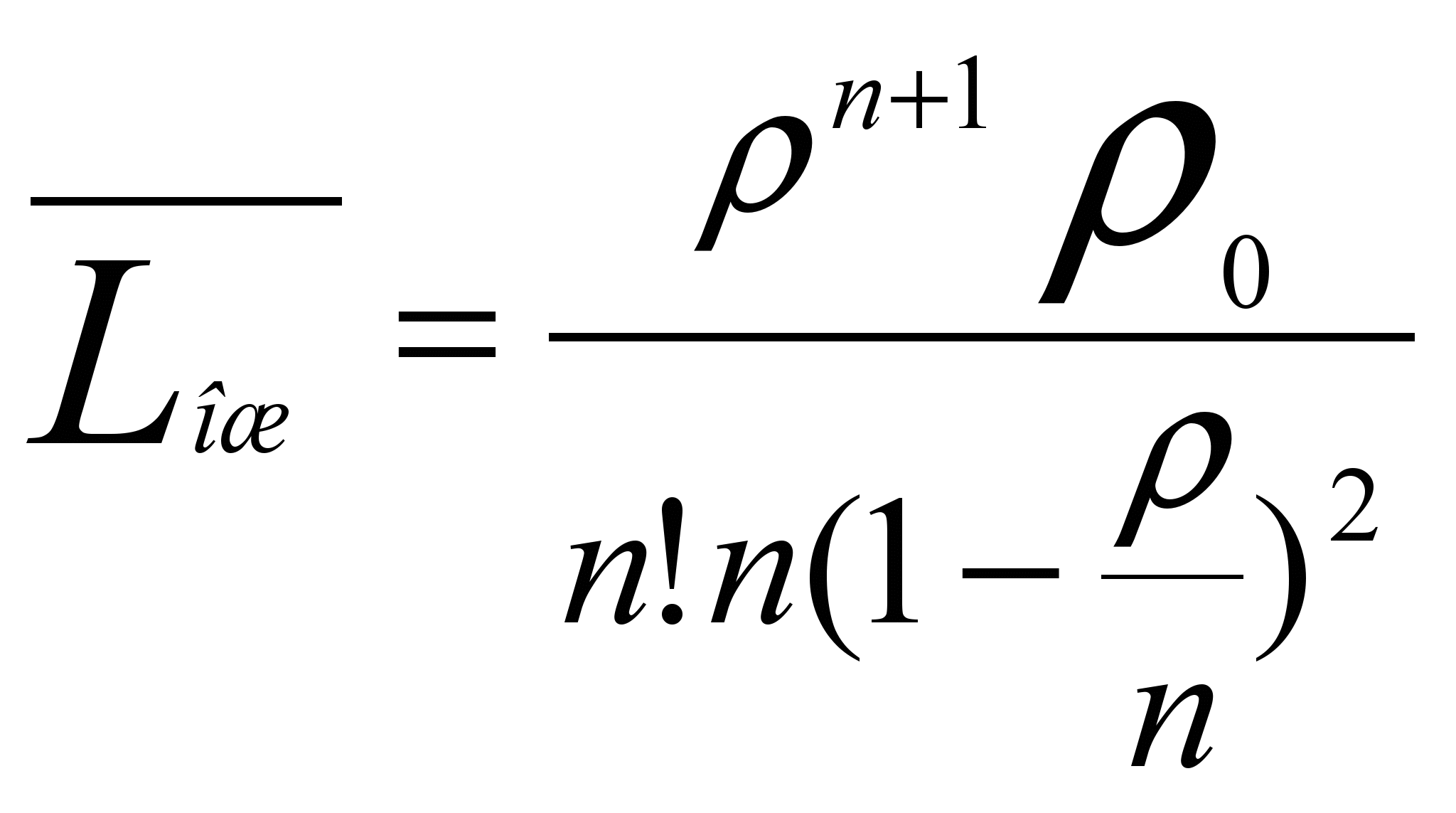
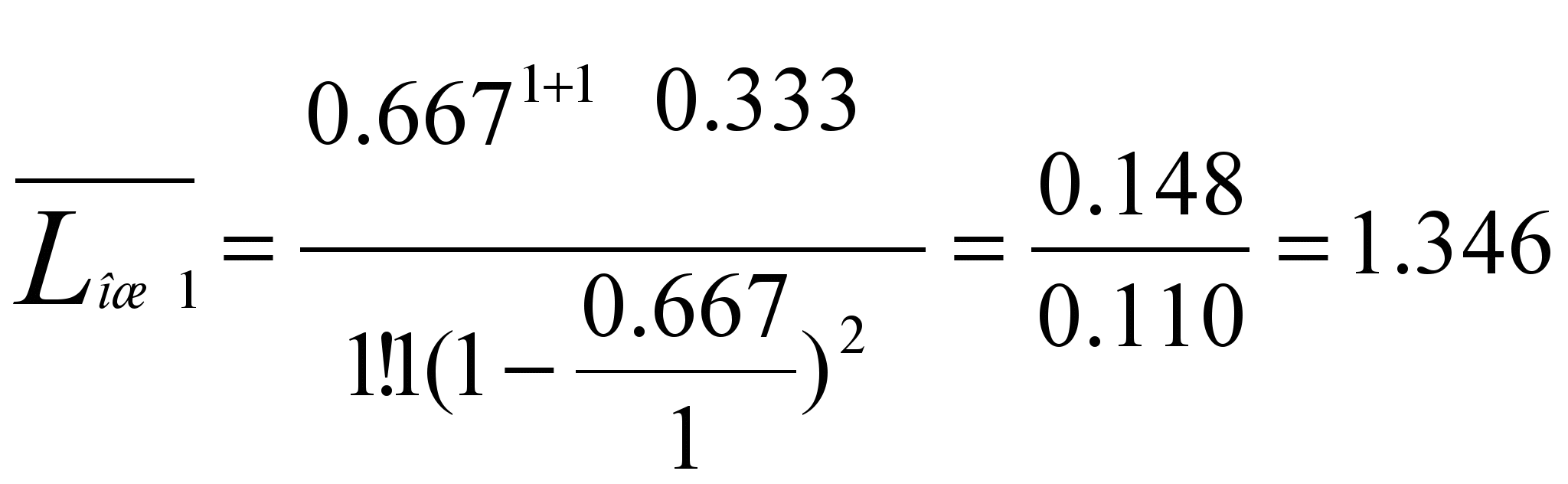
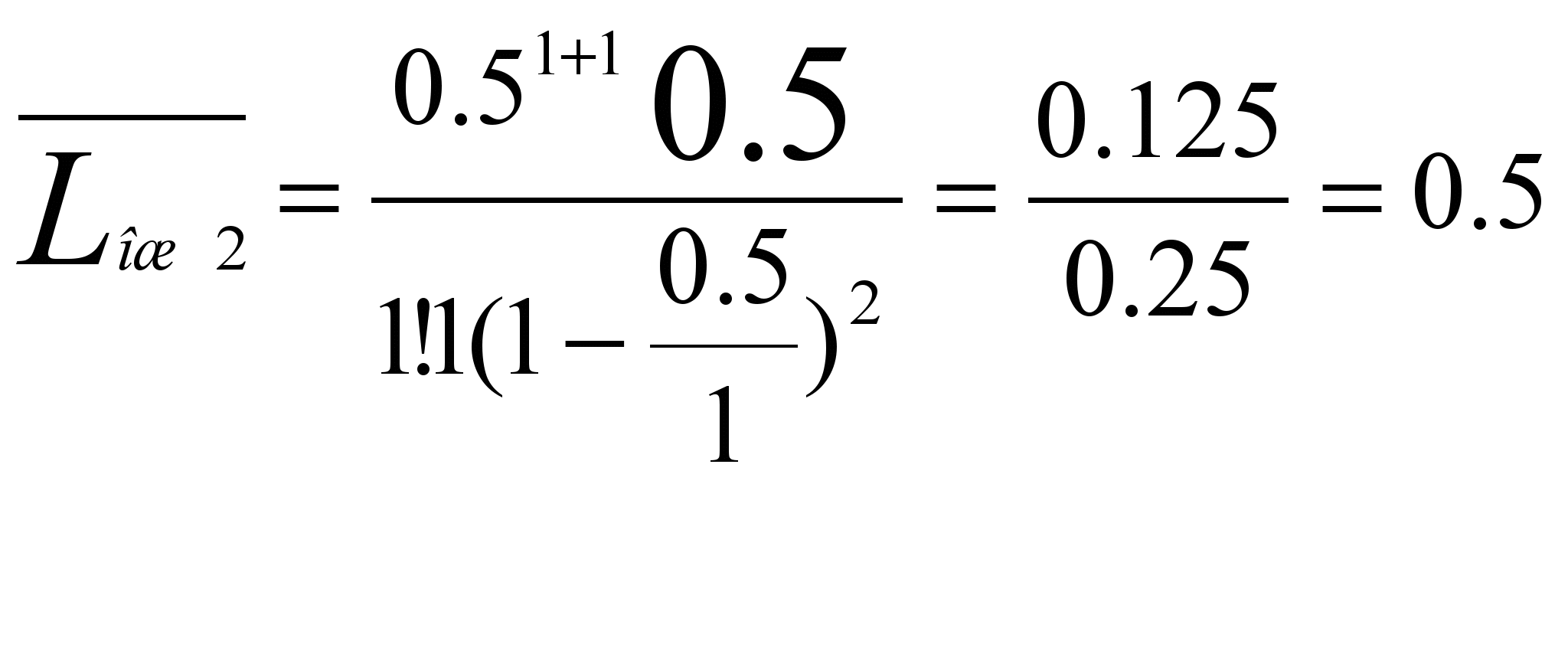
4. Находим среднее число клиентов находящихся в системе:

5. Находим среднее время пребывания клиента в очереди:

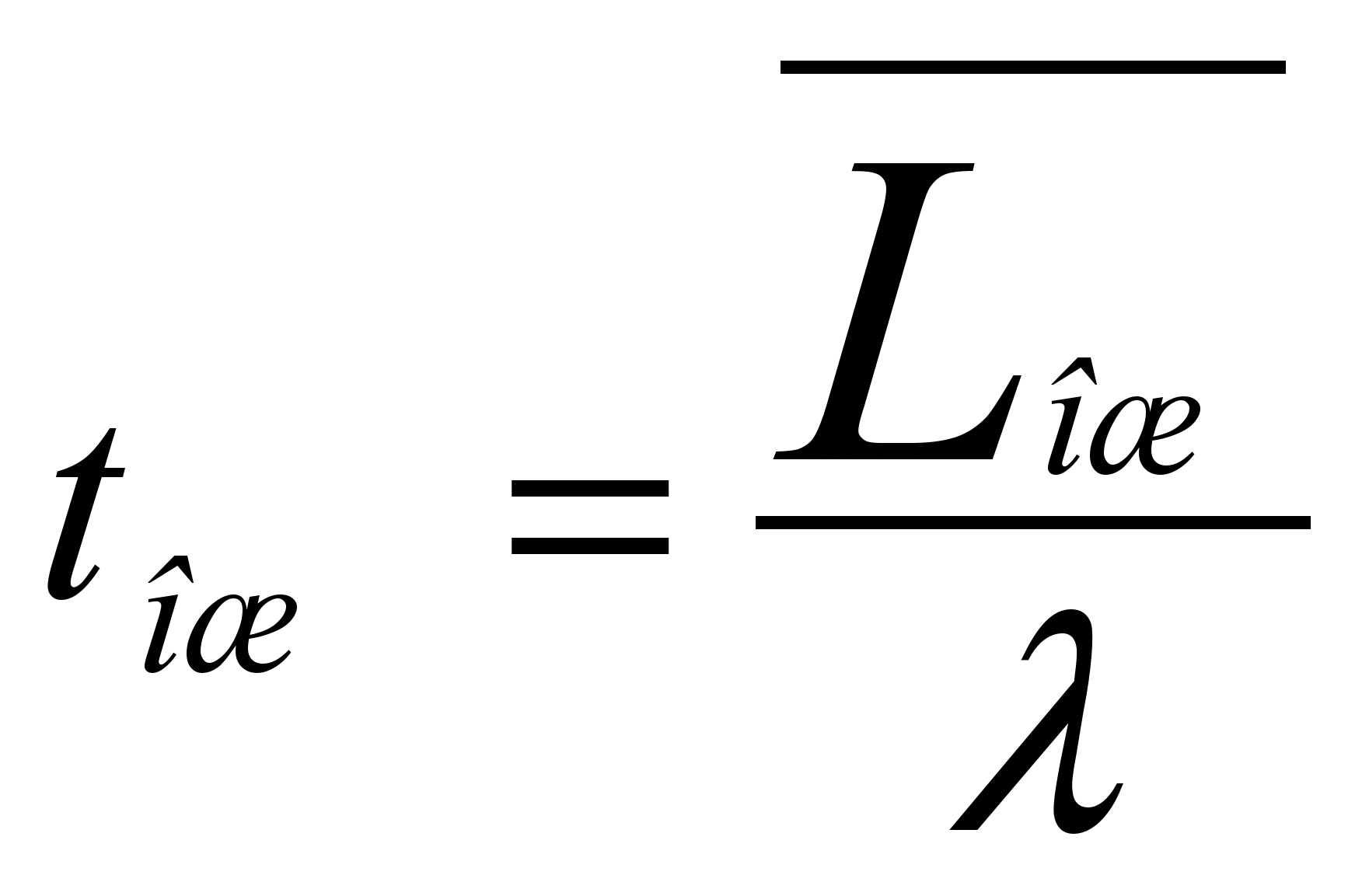
6. Находим среднее время пребывания клиента в системе:

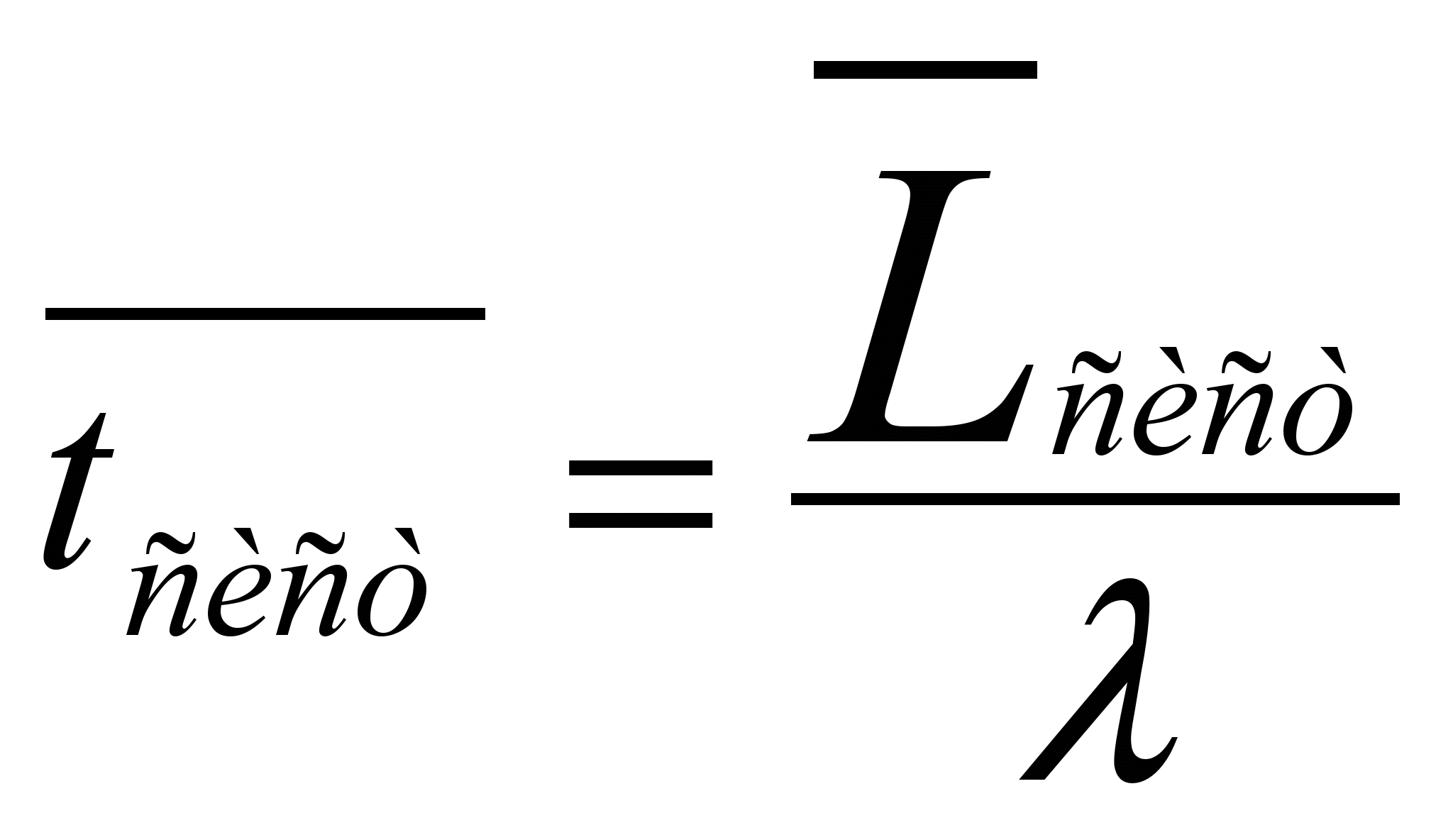
7. Находим среднее число простаивающих каналов:

4. Определяем издержки, связанные с функционированием системы в единицу времени: