1. Введение

2. Основная часть

2.1. Постановка проблемной задачи.

Автосервис решил нанять нового механика для того чтобы он менял старые покрышки на новые. На это место есть 2 кандидата. Один из них имеет ограниченный опыт и может быть нанят за 7 ден. ед /ч. Ожидается, что этот механик сможет обслуживать 3 клиентов в час. Другой механик более опытен, он в состоянии обслуживать 4 клиентов в час, но его можно нанять на работу за 10 ден. ед /ч. Клиенты прибывают соскоростью 2 чел /ч. Предполагая пуассоновское распределение времени прибытия и экспоненциальное распределение продолжительности времени обслуживания, определить:

1.среднее время, которое клиент проводит и очереди;

2.среднюю длину очереди;

3.среднее время, которое клиент проводит в системе обслуживания;

4.среднее число клиентов в системе обслуживания.

5.вероятность того, что система обслуживания окажется незанятой при условии найма одного или другого механика.

Компания оценивает издержки по ожиданию клиентами своей очереди в 15 ден. ед /ч. Какого механика следует нанять, чтобы, обеспечить меньшие совокупные издержки? Каковы минимальные совокупные издержки?

2.2. Построение математической модели задачи.

2.2.1. Формализованное описание модели.

Рассмотрим задачу организации перевозок . Допустим , имеется М пунктов отпровления А1, А2 ,...., Ам , в которых сосредоточены запасы некоторого груза в количествах а1 , а2 , ... , ам едениц соответственно , и N пунктов назначения B1, B2, …, Bn, куда необходимо перевести b₁, b₂,…, bn единиц указанного груза . Стоимость перевозки единицы груза из любого пункта отправления Ai ( i=1,2,…, M ) до любого пункта назначения Bi ( j = 1,2N) равна Cij ( Аi Вj : cij).

Требуется составить план перевозок, суммарная стоимость которых при условии выполнения всех заявок будет минимальной.

В такой постановке показателем эффективности транспортной задачи является суммарная стоимость перевозок, а сама транспортная задача называется транспортной задачей по критерию стоимости.

Обозначим через хij ( i= 1,2,…, M, j =1,2,…, N) количество груза, перевозимого из i- го пункта отправления Ai в j – й пункт назначения Bj ( Ai Bj : xij). Величины хij называются перевозками.

Перевозки х_ij являются управляемыми переменными транспортной задачи. Понятно, что х_ij должны удовлетворять естественным ограничениям

X_ij 0,

так как количество перевозимого груза не может быть отрицательным.

На перевозки x_ij накладываются ограничения, обусловленные количеством перевозимого груза:

количество груза, вывозимого из i – го пункта отправления Ai во все пункты назначения, должно быть не больше запаса груза в пункте назначения aij:

,

,

……………………………

,

…………………………..

;

количество груза, ввозимого в j – й пункт назначения из всех пунктов отправления, должно быть не больше заявки на груз , поданной в пункте назначения :

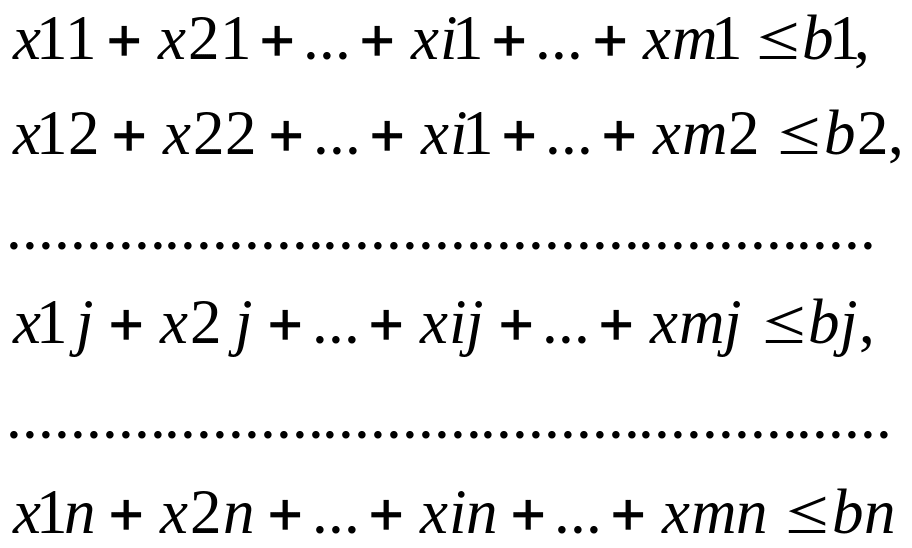
Суммарная стоимость всех перевозок определяется формулой

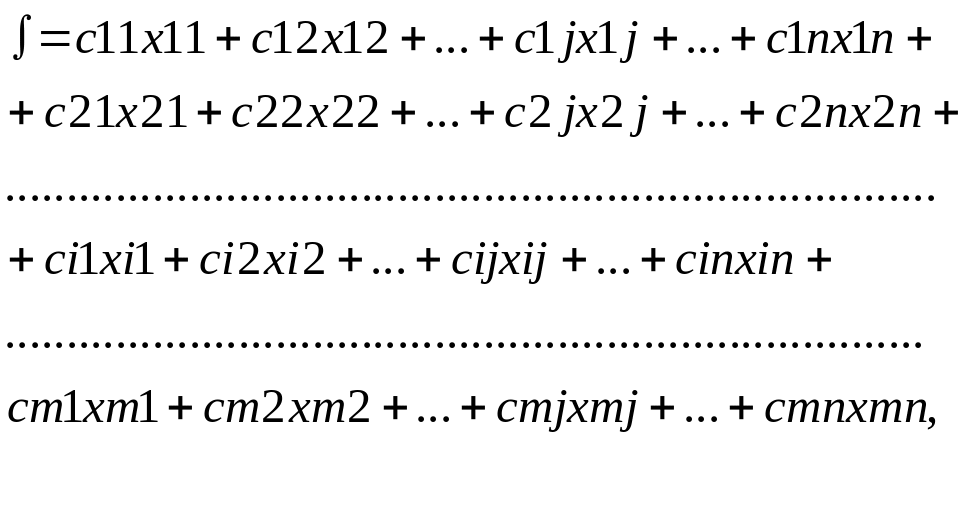
Или короче,

И должно быть минимальна

Совокупность перевозок называется планом перевозок, или

планом. План перевозок называется допустимым, если он удовлетворяет поставленным ограничениям. Допустимый план перевозок называется опорным планом, если в нем отличны от нуля только базисные перевозки. План перевозок называется оптимальным, если соответствующая ему стоимость перевозок минимальна среди всех допустимых планов. Как в любой задачи линейного программирования, оптимальный план является опорным.

Транспортная задача линейного программирования может быть решена более просто из-за того, что коэффициенты при переменных в ограничениях равны единице.

Для решения транспортной задачи составляется транспортная таблица, первые строка и столбец которые соответствуют пунктам отправления и пунктам назначения , последние столбец и строка – запасам в пунктах отправления и заявкам , поданным в пунктах назначения. Нижняя правая клетка таблицы содержит суммарный запас и суммарную заявку . В правый верхний угол внутренних клеток записывается стоимость соответствующих перевозок ( , а в их нужную часть заносятся значения конкретных перевозок , удовлетворяющие поставленным ограничениям. Для того чтобы было удобнее в таблице различать стоимость и перевозки , значение перевозок во всех транспортных таблицах выделены полужирным шрифтом.

Равенство между запасами и ввозимый груз в виде равенств:

Количество груза, вывозимого из пункта отправления А_i во все пункты назначения, должно быть равно запасу груза в пункте назначения а_i.

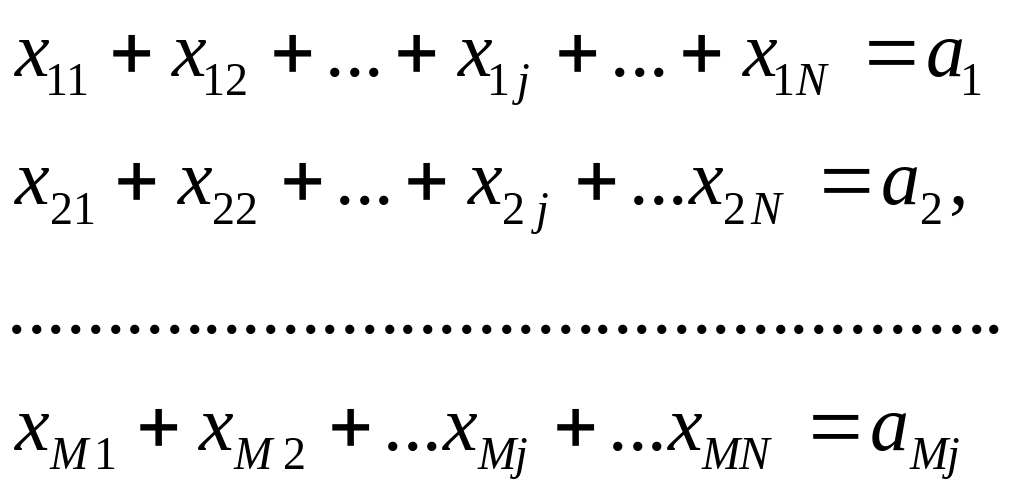
Количество груза, ввозимого в пункт назначения B_j из всех пунктов отправления, должно быть равно заявке на груз b_j поданной в пункте назначения B_j.

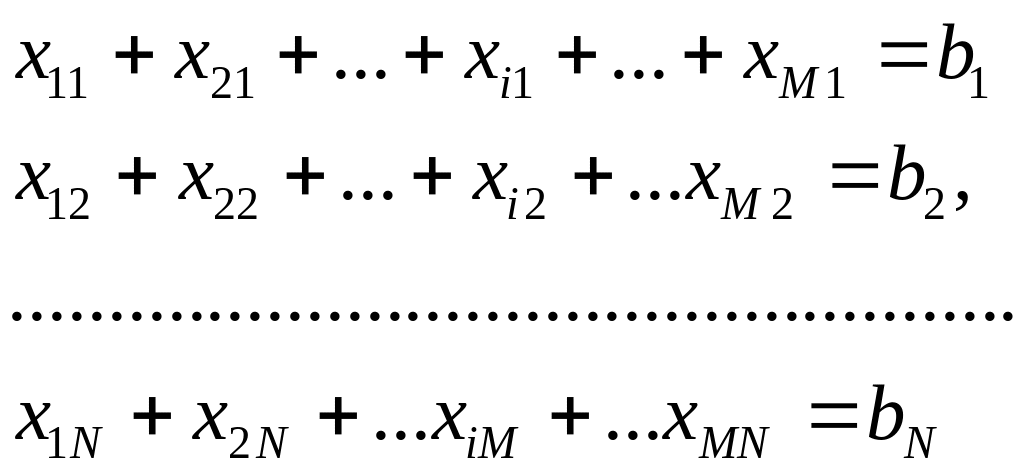
Система ограничения равенств содержит M · N переменных х_ij. Условие баланса приводит к тому, что одно M + N ограничений линейно зависит от других, т.е. ранг системы r = M + N – 1, и сбалансированная транспортная задача должна содержать r базисных переменных. Количество свободных переменных равно р = (М - 1) (N – 1) и, следовательно, р перевозок х_ij равны нулю.

В результате допустимое решение сбалансированной транспортной задачи, т.е. решение, удовлетворяющее ограничениям, может быть получено, если заполнить клетки транспортной таблицы следующим образом:

• Сумма перевозок в каждой строке 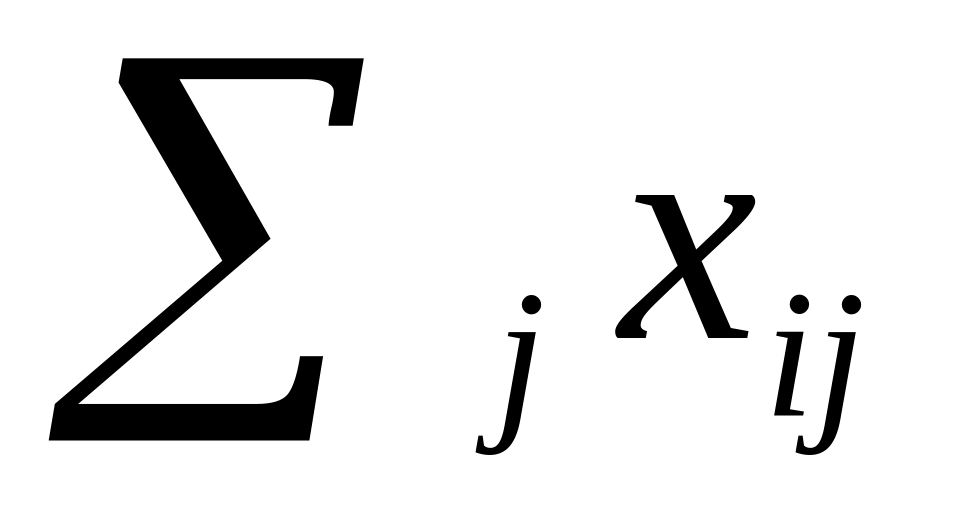была равна запасам соответствующего пункта отправления а_i.

• Сумма перевозок в каждом столбце была равна заявке соответствующего пункта назначения b_i.

Понятно, что так транспортную таблицу можно заполнить разным способом. Искомым решением является то из допустимых решений, для которого общая стоимость перевозок минимальна.

Как для любой линейного программирования, для решения

сбалансированной транспортной задачи, во – первых, необходимо найти какое-то начальное допустимое решение, а затем в результате последовательного итерационного процесса найти оптимальное решение. В отличие от произвольной задачи линейного программирования решение сбалансированной задачи всегда существует.

Для определения начального допустимого решения сбалансированной задачи наиболее часто применяются метод северо-западного угла, метод минимального элемента и метод Фогеля.

В дальнейших разделах, если не оговорено противоположное, всегда рассматривается сбалансированная транспортная задача.