Пример выполнения расчетной работы № 2

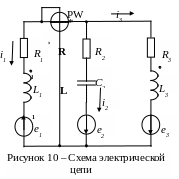Исходные данные:

; ; ;

; , ,

, , .

L₁ - переменный параметр.

РЕШЕНИЕ

1. Система уравнений по первому и второму законам Кирхгофа:

- В дифференциальной форме:

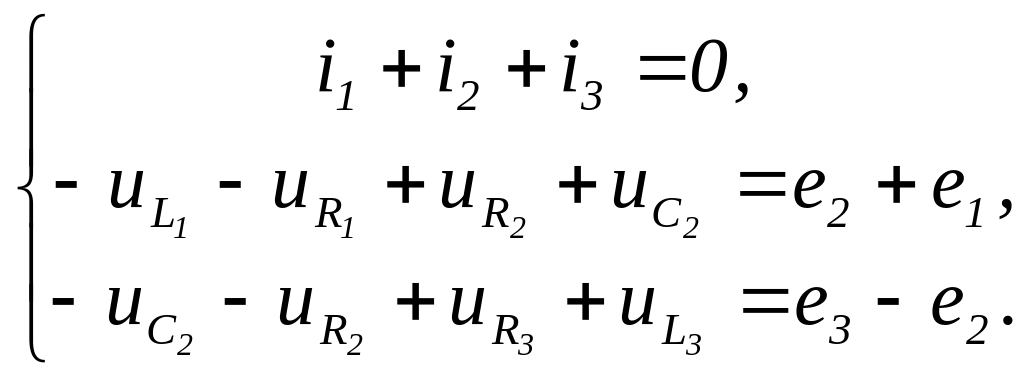
или

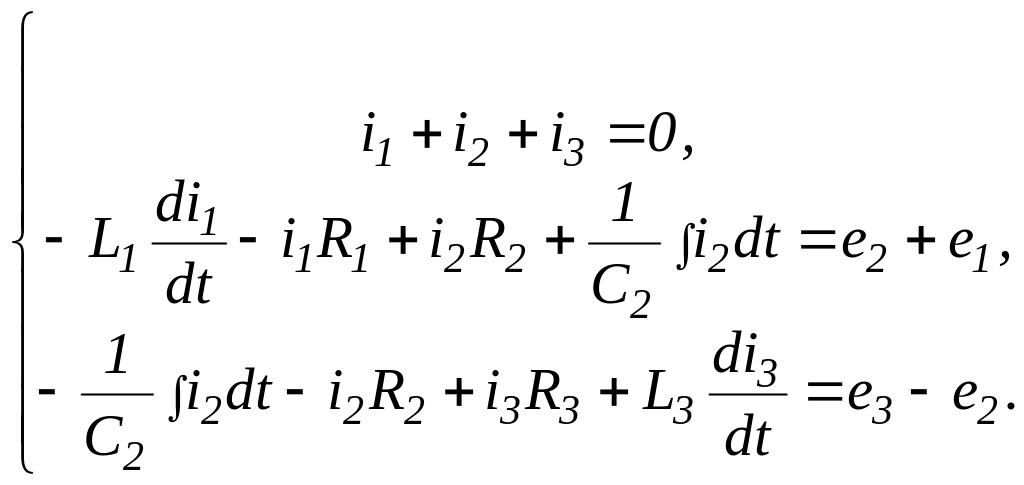
2. Заданная схема электрической цепи с изображением всех параметров, ЭДС и токов в символической форме показана на рисунке 11. Запишем для этой схемы систему уравнений по первому и второму законам Кирхгофа:

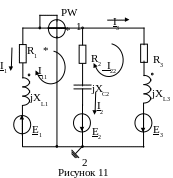
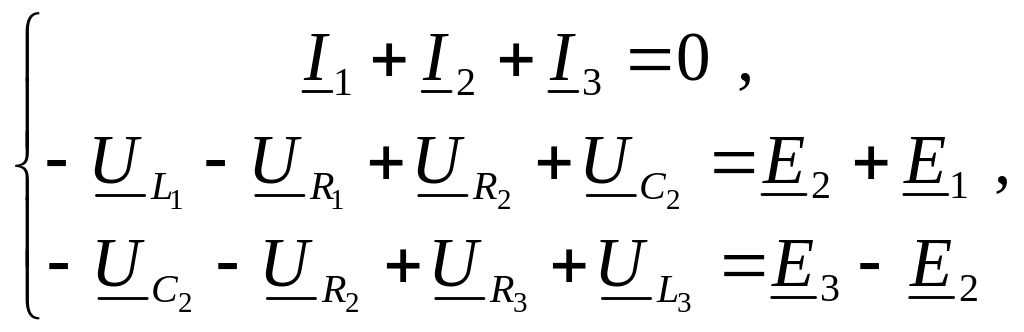
или

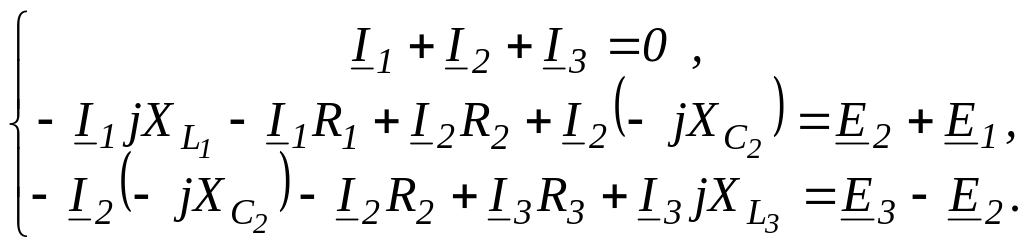
3. Рассчитаем сопротивления и проводимости в символической форме:

; ;

; ;

; ;

; ;

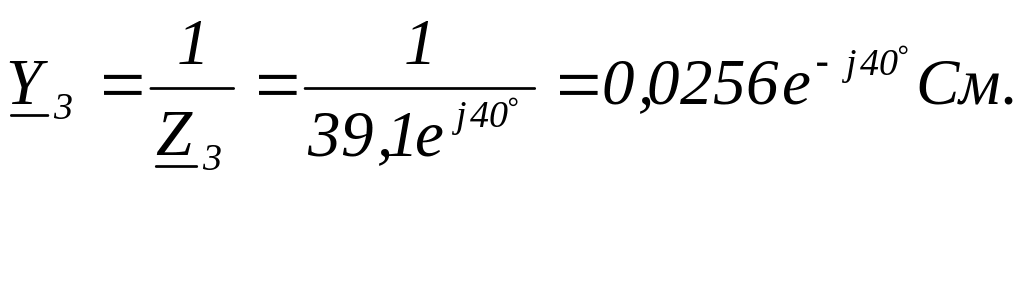
4. Определяем комплексы действующих значений токов I₁₁ и I₂₂ в ветвях двумя методами: методом контурных токов и методом двух узлов.

Метод контурных токов

На схеме электрической цепи наносим контурные токи одного направления I₁₁, I₂₂ , I₃₃ и составляем систему уравнений вида:

В системе уравнений

.

.

.

.

Представим заданные ЭДС в символическом виде:

;

;

.

Тогда

;

.

Подставив значения коэффициентов в систему уравнений, получим

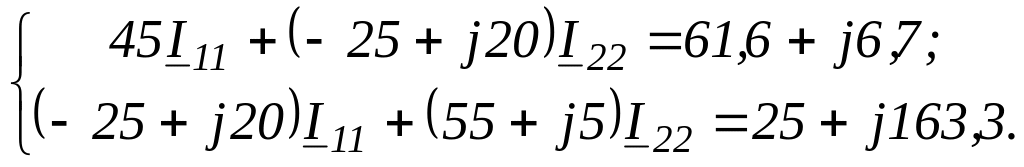
Решим систему уравнений:

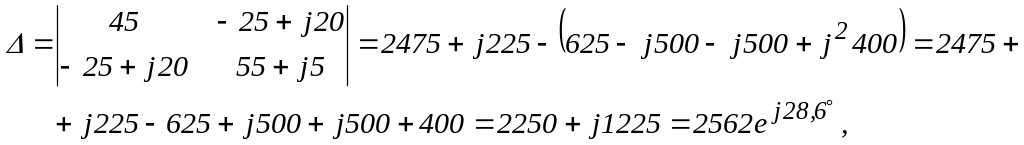
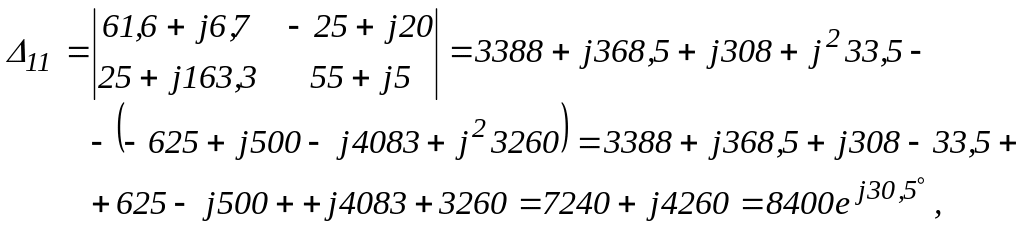
Значения контурных токов:

, .

Действительные комплексы токов в ветвях электрической цепи будут равны:

,

,

Метод двух узлов

Определим напряжение между узлами 1 и 2:

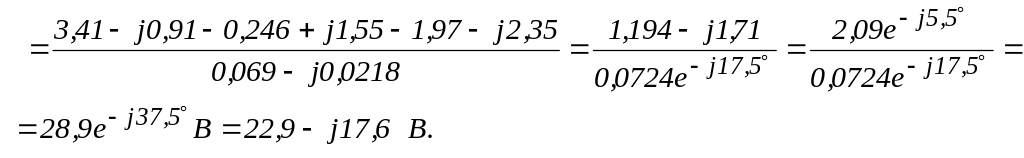Составим уравнения по второму закону Кирхгофа для каждой ветви, замкнутой напряжением U₁₂:

• для первой ветви:

,

откуда

• для второй ветви:

,

тогда

;

• для третьей ветви:

,

откуда

.

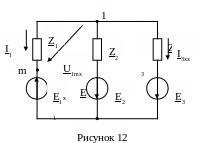
5. Определим ток в ветви с переменным параметром L₁ методом активного двухполюсника (эквивалентного генератора) (рисунок 12). Схема для определения входного сопротивления показана на рисунке 13.

.

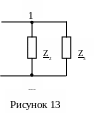
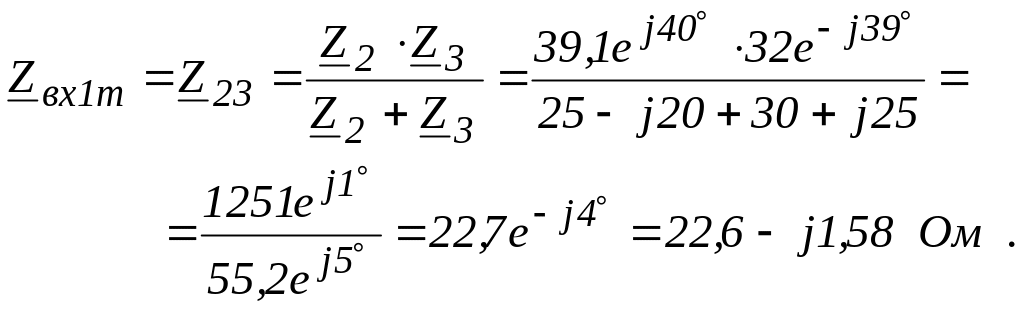
6. Значения всех токов, определенных разными методами, занести в таблицу и сравнить их.

	I1,A	I2,A	I3,A
Метод контурных токов
Метод двух узлов
Метод активного двухполюсника		____	_____

Значения токов, полученные разными методами, приблизительно одинаковы. Небольшие несоответствия можно объяснить погрешностью расчетов. Использование того или иного метода выбирается исходя из условия задачи и поставленной конечной цели.

7. Определить показание ваттметра.

.

.

.

8. Построить топографическую диаграмму напряжений, совмещенную с векторной диаграммой токов. Заземлим узел 2, то есть присвоим ему потенциал, равный нулю. Рассчитываются потенциалы всех точек электрической цепи (обозначены на рисунке 14).

Пусть . Тогда

Примем масштаб напряжений и токов равный: ; .

О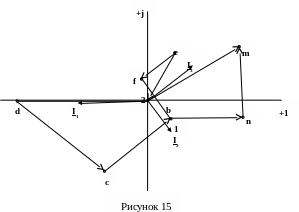 тложим на комплексной плоскости значения потенциалов и соединим их отрезками. Напряжение между любыми двумя точками можно определить по топографической диаграмме. Топографическая диаграмма показана на рисунке 15.

9. Составим систему уравнений по законам Кирхгофа в дифференциальной и символической форме с учетом магнитной связи между катушками индуктивности (начало обмоток выбрать произвольно см. рисунок 11).

В дифференциальной форме:

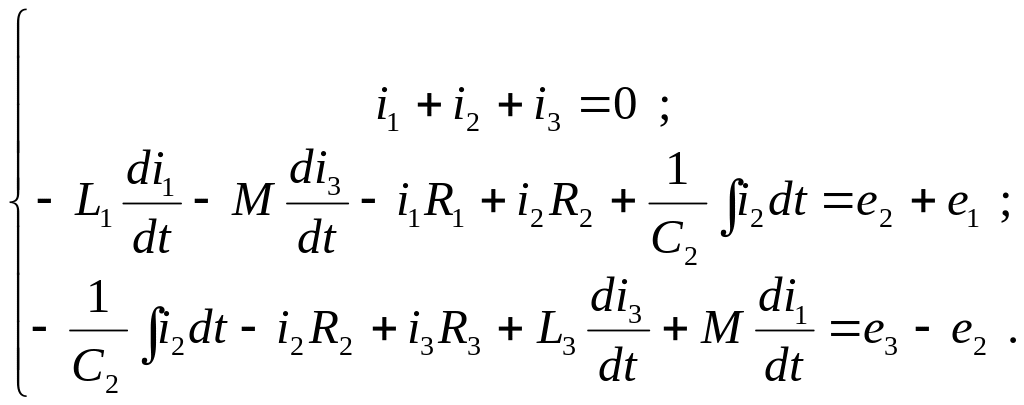
В символической форме:

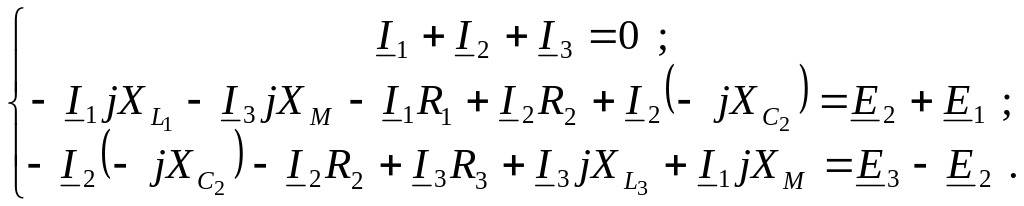
или

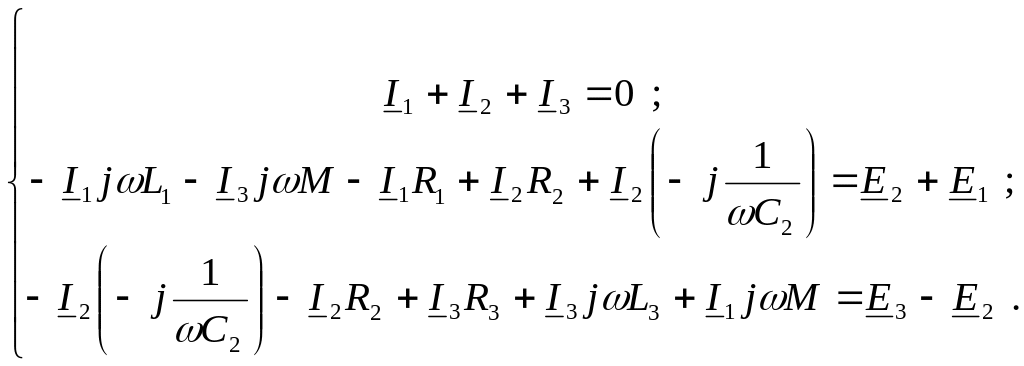
10. Построить круговую диаграмму для тока I₁ , если L₁=Var.

По методу эквивалентного генератора можно записать:

где

.

Подставив U_nmxx и Z_вх, получим уравнение для тока I₁, представляющее собой уравнение окружности, проходящей через начало координат:

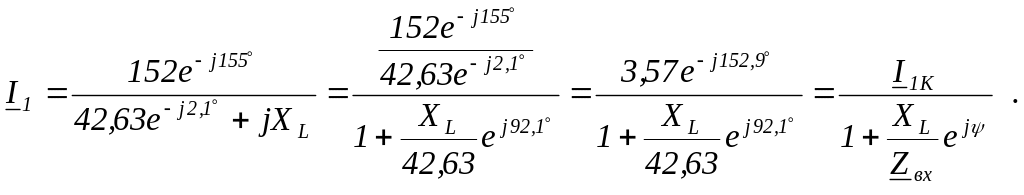
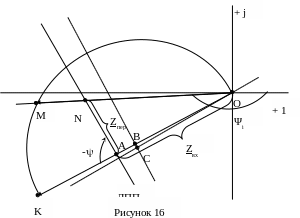Для построения круговой диаграммы выберем масштаб для тока m_i=0.5 А/см, для сопротивлений - m_c=10 Ом/см. Начальная фаза искомого тока Ψ_i = -177^о. Круговая диаграмма приведена на рисунке 16.

Из круговой диаграммы при X_L1=20 Ом,

МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ

ПО ВЫПОЛНЕНИЮ РАСЧЕТНОЙ РАБОТЫ № 3 на тему