Метод двух узлов. Метод является частным случаем метода узловых потенциалов. Для расчета составляется только одно уравнение.

Область применения. Метод используется, когда ЭЦ имеет несколько параллельных ветвей и только два узла.

Сущность метода заключается в том, что при расчете определяют разность потенциалов между двумя узлами, затем по закону Ома вычисляют токи в ветвях. Порядок расчета следующий:

• Напряжение между двумя узлами вычисляется по формуле

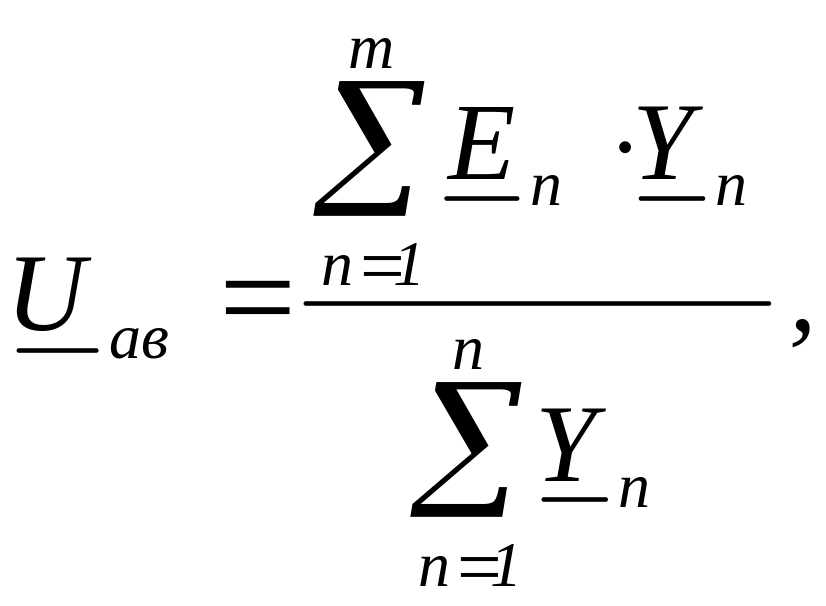
где Е_n – комплекс ЭДС n-ой ветви (если направлена к узлу «а», то имеет

знак плюс, если от узла – то знак минус);

Y_n – комплексная проводимость n-ой ветви;

n – число параллельных ветвей;

m – число ветвей, содержащих ЭДС.

• Токи в ветвях определяют по закону Ома с учетом известного уже напряжения на зажимах каждой ветви.

Методом эквивалентного генератора задача решается также, как описано выше на странице 12, при расчете все токи напряжения и сопротивления подставляются в комплексной форме.

Для определения показаний ваттметра, установленного в электрической цепи, следует помнить, что он показывает скаляр, равный произведению трех величин:

,

где U – действующее значение напряжения на обмотке напряжения ватт-

метра;

I – действующее значение тока в токовой обмотке ваттметра;

_u – начальная фаза напряжения U;

_i – начальная фаза тока I.

Для построения топографической диаграммы предварительно определяют комплексные значения всех токов электрической цепи. Найденные комплексные токи откладывают на комплексной плоскости в выбранном масштабе.

Маркируют все точки электрической цепи, одну из них условно заземляют, то есть присваивают ей потенциал, равный нулю. Эта точка будет располагаться в начале координат комплексной плоскости. Рассчитывают потенциалы каждой точки электрической цепи. Выбирают масштаб потенциалов и каждую точку цепи наносят на комплексную плоскость. Точки, имеющие прямую электрическую связь, соединяют прямыми линиями.

Таким образом, каждой точке электрической цепи будет соответствовать точка на комплексной плоскости. Разность потенциалов между двумя любыми точками электрической цепи может быть определена по топографической диаграмме. Для этого следует соединить вектором соответствующие точки на комплексной плоскости.

В расчетной работе требуется построить круговую диаграмму тока в той ветви, для которой определялся ток методом активного двухполюсника (эквивалентного генератора).

Предполагается, что ЭДС электрической цепи неизменны по модулю и фазе, а заданная нагрузка Z_Х в ветви изменяется только по модулю. Известно, что в этом случае для тока I_Х может быть построена круговая диаграмма, поскольку он проходит непосредственно через переменное сопротивление.

В данной работе при расчете тока в той же ветви методом эквивалентного генератора вся электрическая цепь относительно ветви с искомым током представляется в виде активного двухполюсника с внутренним сопротивлением Z_вх относительно зажимов двухполюсника а-в. При этом ток рассчитывался по формуле:

Разделив числитель и знаменатель первой части уравнения на Z_вх, получим

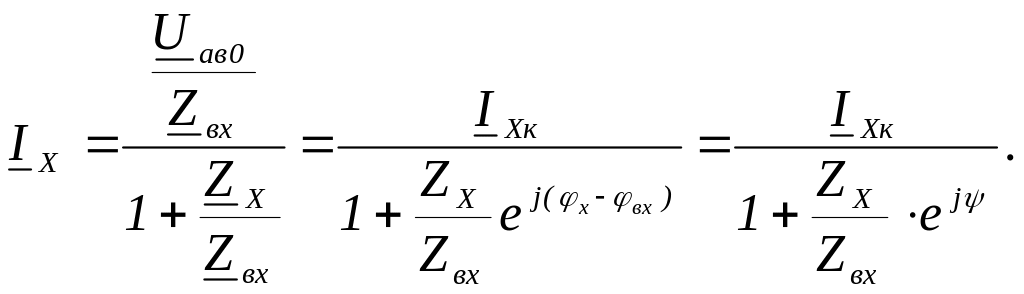
Из этого уравнения следует, что конец вектора тока I_Х скользит по дуге окружности, проходящей через начало координат, хордой которой является вектор тока I_Хк. Из уравнения также видно, что для построения круговой диаграммы необходимо определить:

• ток короткого замыкания I_Хк;

• сопротивление короткого замыкания Z_вх;

• угол  = _Х - _вх.

Значения тока I_Хк, его начальная фаза _Хк, сопротивление Z_вх и угол _вх определяют в расчете тока в данной ветви методом эквивалентного генератора.

Круговая диаграмма приведена на рисунке 9. Порядок ее построения следующий:

• Произвольно выбирают масштабы напряжений m_U, токов m_I, сопротивлений m_Z.

• В осях координат строят ток I_Хк - вектор ОК.

• От точки О на хорде ОК в масштабе m_Z откладывают модуль сопротивления Z_вх (отрезок ОА).

• Через точку А под углом минус  к хорде ОК проводят рабочую часть линии переменного параметра.

• Определяют центр окружности, дуга которой является геометрическим местом конца вектора тока I_Х. Центром окружности является точка С пересечения двух перпендикуляров, один из которых восстанавливается к

середине хорды (точка В), а второй опускается из точки О на линию переменного параметра или ее продолжение.

• Проводят дугу круговой диаграммы, она ограничена хордой ОК и лежит с той стороны хорды, где расположена рабочая часть линии переменного параметра. Диаграмма готова.

Для определения значения тока I_Х при заданном значении сопротивления ветви Z_X (переменного параметра, указанного в задании) вдоль линии

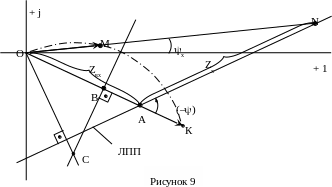
переменного параметра от точки А в сторону отложенного угла минус ψ откладывают в масштабе сопротивлений значение заданного сопротивления

Z_X – отрезок АN. Соединяют начало координат (точку О) с точкой N и находят точку М пересечения прямой ОN с окружностью круговой диаграммы. Соединив точку М с точкой О, получают вектор ОМ, который в масштабе токов представляет собой значение тока в ветви при заданном сопротивлении, то есть

,

значение начальной фазы тока получают измерением транспортиром угла между этим вектором и действительной осью на комплексной плоскости.