Пример выполнения расчетной работы № 6

И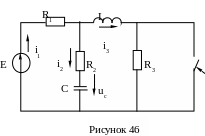 сходные данные:

E = 60 В;

L = 20 мГн;

С = 100 мкФ;

R₁ = 60 Oм;

R₂ = 20 Oм;

R₃ = 60 Oм.

Искомая величина i₁.

Классический метод расчета переходного тока i₁

Для электрической цепи на рисунке 46 составим систему уравнений по законам Кирхгофа:

(21)

(22)

(23)

Дл упрощения дальнейших расчетов решаем систему относительно , так как переходной процесс един для всей цепи.

Из уравнения (22) с учетом того, что , получим

Решим это уравнение относительно тока i₁.

(24)

Из уравнения (21) получим

. (25)

Подставим (24) и (25) в уравнение (23)

,

.

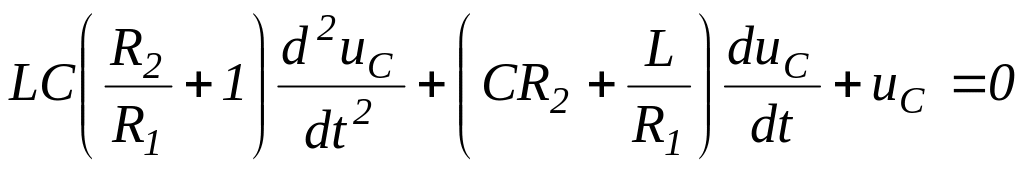От полученного в результате преобразований последнего уравнения перейдем к характеристическому уравнению послекоммутационной цепи:

;

подставив значения параметров из условия задания, получим

.

Решив данное квадратное уравнение, найдем корни характеристического уравнения

.

Так как корни характеристического уравнения получились комплексными сопряженными, представим решение задачи в виде:

или

Здесь

Для определения постоянных интегрирования составим систему уравнений:

.

П ри t = 0

;

.

Определим начальные условия:

1. Независимые начальные условия (Н.Н.У.):

2. Зависимые начальные условия (З.Н.У.):

,

из уравнения (22) получим

;

;

;

.

Продифференцируем уравнение (21)

– – = 0;. (26)

Из (23) определим

= . (27)

Дифференцируем уравнение (22)

+ + ;

= . (28)

Подставляя (27) и (28) в (26), получим

;

;

4 = ;

= 375.

Таким образом, для момента коммутации цепи получим два уравнения:

Решим систему, разделив второе уравнение на первое:

,

,

.

Подставив значение  в первое уравнение системы, получим:

В итоге получаем значение искомого тока:

Для построения временной диаграммы вычислим величину

Определим период колебания:

П остроенная временная диаграмма приведена на рисунке 47.

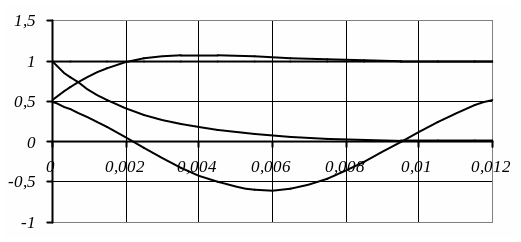
Рисунок 47

Операторный метод расчета переходного тока i₁

С оставим операторную схему замещения электрической цепи (рисунок 48).

Определив эквивалентные ЭДС Еэ(р) и сопротивление Zэ(р) двух параллельных ветвей, упростим схему на рисунке 48 и получим схему на рисунке 49.

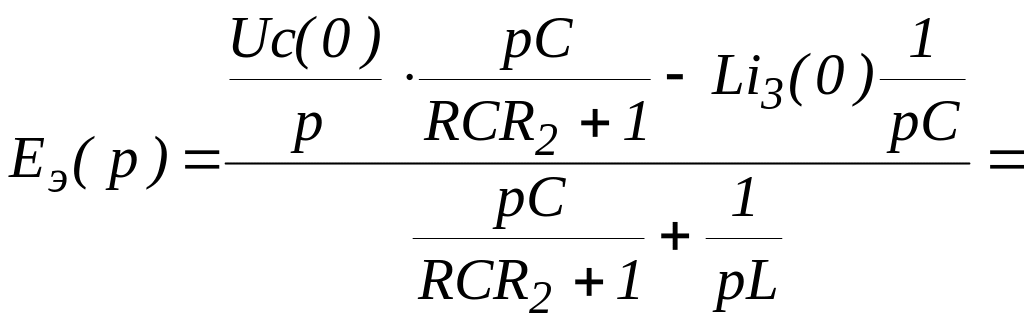
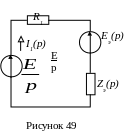
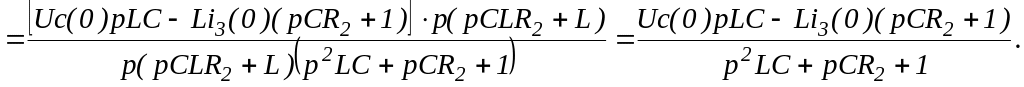
Эквивалентную проводимость ветвей и их эквивалентное сопротивление определим следующим образом:

;

.

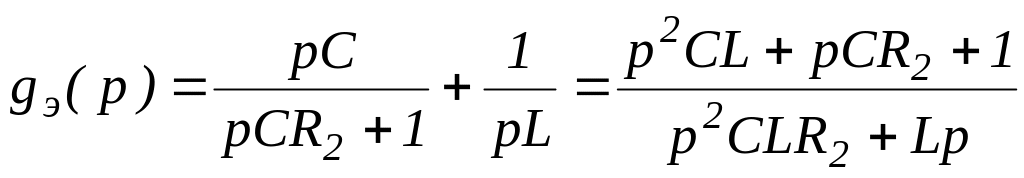Тогда изображение искомого тока будет:

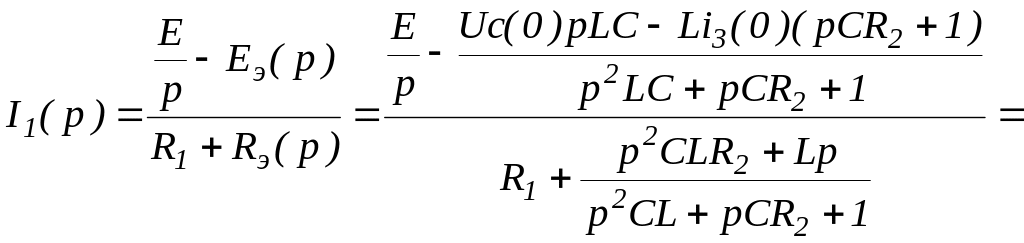
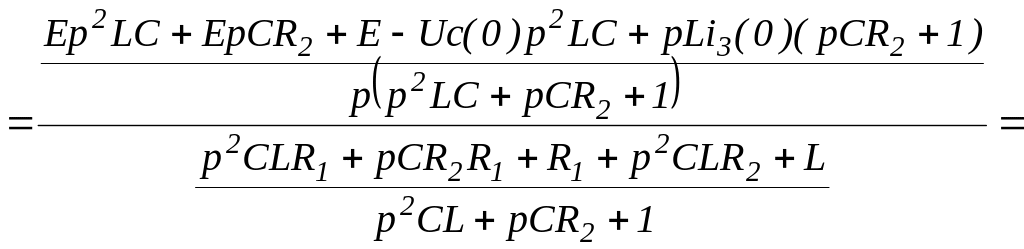
Приравняем знаменатель нулю и найдем его корни

После преобразований получим: , откуда .

Перейдем от изображения к оригиналу:

.

Здесь .

Так как , а , то