
- •Теоретические основы электротехники учебно-методическое пособие по выполнению расчетных работ
- •Зерноград, 2004
- •Общие сведения
- •Методические указания
- •Основная литература
- •Дополнительная литература
- •Методические рекомендации по выполнению
- •Электрическая цепь постоянного тока
- •Порядок расчета:
- •Метод эквивалентного генератора (или метод активного двухполюсника, или метод холостого хода и короткого замыкания).
- •Пример выполнения расчетной работы № 1
- •Методические рекомендации по выполнению расчетной работы № 2 на тему Электрическая цепь синусоидального тока
- •Метод двух узлов. Метод является частным случаем метода узловых потенциалов. Для расчета составляется только одно уравнение.
- •Пример выполнения расчетной работы № 2
- •- В дифференциальной форме:
- •В системе уравнений
- •Подставив значения коэффициентов в систему уравнений, получим
- •Метод двух узлов
- •Электрическая цепь трехфазного тока
- •Пример выполнения расчетной работы № 3
- •6. Разложение на симметричные составляющие.
- •Несинусоидальные токи в трехфазных цепях
- •П ример выполнения расчетной работы № 4
- •Определим мгновенные значения эдс по фазам.
- •Магнитная цепь постоянного тока
- •Пример выполнения расчетной работы № 5
- •Переходные процессы в линейных электрических цепях
- •1. Если .
- •2. Если .
- •3. Если ,
- •Пример выполнения расчетной работы № 6
- •Оглавление
Пример выполнения расчетной работы № 5
Исходные данные:
Д ля
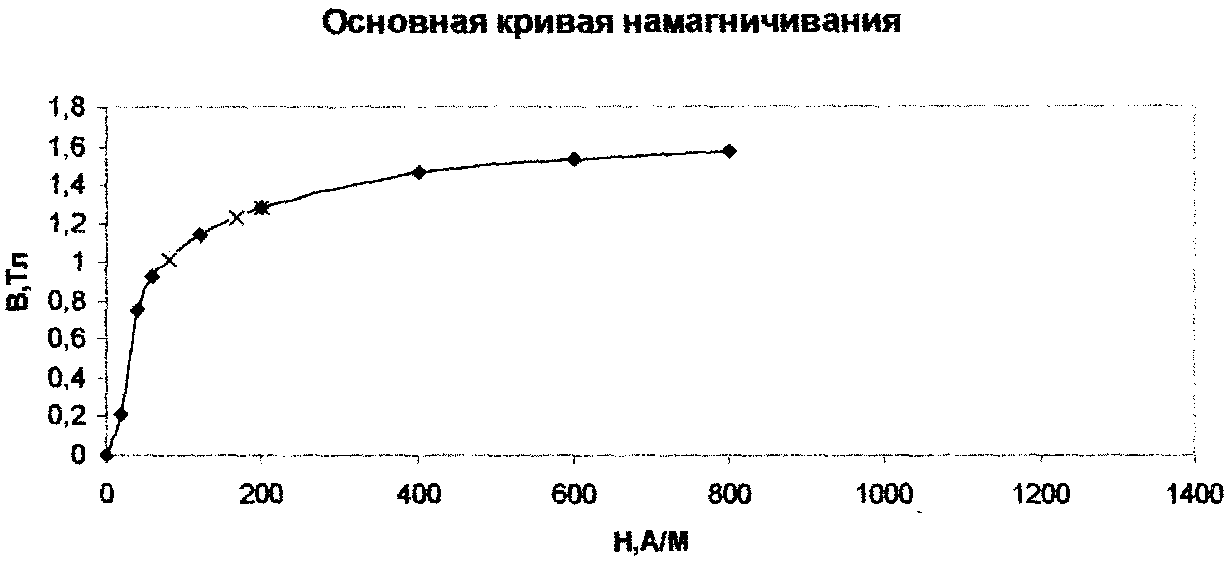
магнитной цепи (рисунок 36), основная
кривая намагничивания магнитопровода
которой задана (рисунок 37), требуется
определить ток I2,
и магнитный поток Ф3.
ля
магнитной цепи (рисунок 36), основная
кривая намагничивания магнитопровода
которой задана (рисунок 37), требуется
определить ток I2,
и магнитный поток Ф3.
Размеры магнитопровода:
L1 = 28 см; S1 = 4 см2 ;
L2 = 8 см; S2 = 7 см2;
L3 = 28 см; S3 = 10 см2 ;
параметры катушек:
W1 = 80; I1 = 0,25 А; W2 = 275;
W3 = 320; I3 = 0,25 А.
Дополнительные условия: Ф2 –Ф1 = 20·10-4 Вб.
РЕШЕНИЕ
Для решения задачи выберем положительные направления магнитных потоков и укажем их на рисунке магнитопровода.
Составим уравнения по первому и второму законам Кирхгофа для магнитной цепи:
Ф1 + Ф2 – Ф3 = 0; (10)
I1W1 -I2W2= H1L1 –H2L2;
I3W3 + I2W2= H3L3 +H2L2.
Поскольку по своей постановке имеем обратную задачу, то решаться она будет методом графоаналитическим. Для ее решения и построения вебер-амперных характеристик составим уравнения по второму закону Кирхгофа для каждой из ветвей, охваченной падением магнитного напряжения
между двумя узлами Uмdk.
Рисунок 37
Для первой ветви: I1W1= Uмdk + H1L1; тогда Uмdk = I1W1 - H1L1 .
Для второй ветви: I2W2= Uмdk + H2L2; откуда Uмdk = I2W2-Н2L2.
Для третьей ветви: I3W3= - Uмdk + H3L3; тогда Uмdk = - I3W3 +H3L3.
В полученных уравнениях: H1, H2, H3 – напряженности магнитного поля соответственно в ветвях 1, 2, 3; L1, L2, L3 – длина средней силовой линии каждой ветви.
Задаваясь различными значениями магнитных потоков Ф1 в ветви 1, определим соответствующие им значения магнитной индукции по формуле:
![]() ,
,
занесем эти значения в таблицу 1, затем по кривой намагничивания – значения, соответствующих напряженностей магнитного поля Н1.
Используя полученные ранее выражения для падения магнитного напряжения между узлами для ветви 1 рассчитываем величину Uмdk для каждой строки таблицы 1.
Таблица 1
Ф1, 10-4, Вб |
В1, Тл |
Н1, А/м |
Н1L1, А |
UMdk=I1W1-H1L1, А |
0 |
0 |
0 |
0 |
20 |
0,88 |
0,22 |
20 |
5,6 |
14,4 |
3 |
0,75 |
40 |
11,2 |
8,8 |
3,72 |
0,83 |
60 |
16,8 |
3,2 |
4,08 |
1,02 |
80 |
22,4 |
-2,4 |
4,56 |
1,14 |
120 |
33,6 |
-13,6 |
5,12 |
1,28 |
200 |
56 |
-36 |
5,88 |
1,47 |
400 |
112 |
-92 |
6,12 |
1,53 |
600 |
168 |
-148 |
6,28 |
1,57 |
800 |
224 |
-204 |
Аналогичные расчеты выполним для ветви 3. Результаты расчета представлены в таблице 2.
Таблица 2
Ф3, 10-4, Вб |
В3, Тл |
Н3, А/м |
Н3L3, А |
UMdk=-I3W3+H3L3, А |
0 |
0 |
0 |
0 |
-80 |
2,2 |
0,22 |
20 |
5,6 |
-74,4 |
7,5 |
0,75 |
40 |
11,2 |
-68,8 |
9,3 |
0,83 |
60 |
16,8 |
-63,2 |
10,2 |
1,02 |
80 |
22,4 |
-57,6 |
11,4 |
1,14 |
120 |
333,6 |
-46,4 |
12,8 |
1,28 |
200 |
56 |
-24 |
14,7 |
1,47 |
400 |
112 |
32 |
15,3 |
1,53 |
600 |
168 |
88 |
15,7 |
1,57 |
800 |
224 |
144 |
Поскольку по условию задачи неизвестен ток I2, то веберамперную характеристику для второй ветви табличным методом рассчитать не удастся.
Воспользуемся для решения задачи дополнительным условием –
Ф2-Ф1 = 20·10-4 Вб.
Построим веберамперные характеристики по данным таблиц 1 и 2 (рисунок 38).
Рисунок 38
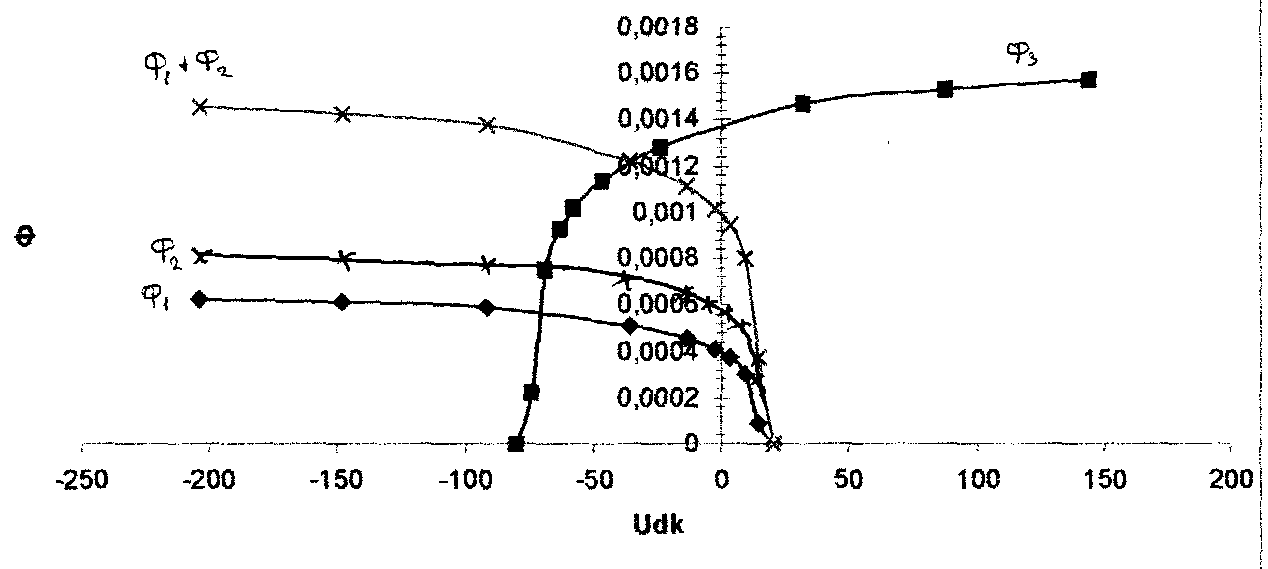
Точка пересечения веберамперных характеристик ветвей, соответствующая значению Umdk = - 36 А, есть решение задачи. При этом падении магнитного напряжения между узлами определим значения магнитных потоков, магнитных индукций и напряженностей магнитного поля в ветвях:
Ф1 = 5,12·10-4 Вб; Ф2 = 7,12·10-4 Вб; Ф3 = 12,24·10-4 Вб.
Соответствующие им значения магнитной индукции равны:
В1 = 1,28 Тл; В2 = 1,017 Тл; В3 = 1,224 Тл.
По основной кривой намагничивания по значениям магнитной индукции определим напряженности магнитного поля в стержнях магнитопровода:
Н1 = 200 А/м; Н2 = 80 А/м; Н3 = 167 А/м.
Из уравнения I2W2 = Uмdk +Н2L2 получим, подставив значения напряженности магнитного поля, во втором стержне магнитопровода Н2 и число витков второй катушки W2 , что I2 = 0,108 А.
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ ПО ВЫПОЛНЕНИЮ
РАСЧЕТНОЙ РАБОТЫ № 6 на тему
