- •Теоретические основы электротехники учебно-методическое пособие по выполнению расчетных работ
- •Зерноград, 2004
- •Общие сведения
- •Методические указания
- •Основная литература
- •Дополнительная литература
- •Методические рекомендации по выполнению
- •Электрическая цепь постоянного тока
- •Порядок расчета:
- •Метод эквивалентного генератора (или метод активного двухполюсника, или метод холостого хода и короткого замыкания).
- •Пример выполнения расчетной работы № 1
- •Методические рекомендации по выполнению расчетной работы № 2 на тему Электрическая цепь синусоидального тока
- •Метод двух узлов. Метод является частным случаем метода узловых потенциалов. Для расчета составляется только одно уравнение.
- •Пример выполнения расчетной работы № 2
- •- В дифференциальной форме:
- •В системе уравнений
- •Подставив значения коэффициентов в систему уравнений, получим
- •Метод двух узлов
- •Электрическая цепь трехфазного тока
- •Пример выполнения расчетной работы № 3
- •6. Разложение на симметричные составляющие.
- •Несинусоидальные токи в трехфазных цепях
- •П ример выполнения расчетной работы № 4
- •Определим мгновенные значения эдс по фазам.
- •Магнитная цепь постоянного тока
- •Пример выполнения расчетной работы № 5
- •Переходные процессы в линейных электрических цепях
- •1. Если .
- •2. Если .
- •3. Если ,
- •Пример выполнения расчетной работы № 6
- •Оглавление
П ример выполнения расчетной работы № 4
Исходные данные:
R=4,2 Ом;
L = 7,5·10-3 Гн;
С=37,5·10-6 Ф;
точки с, N’.
Схема электрической цепи приведена на рисунке 29.
Значения заданной несинусоидальной периодической функции e(ωt)
ωt |
0 |
15 |
30 |
45 |
60 |
75 |
90 |
105 |
e(ωt) |
175 |
194,7 |
173 |
139,9 |
125 |
139,3 |
173 |
194 |
|
|
|
|
|
|
|
|
|
ωt |
120 |
135 |
150 |
165 |
180 |
195 |
210 |
225 |
e(ωt) |
175 |
104,8 |
0 |
-104,8 |
-175 |
-194,6 |
-173 |
-139,9 |
|
|
|
|
|
|
|
|
|
ωt |
240 |
255 |
270 |
285 |
300 |
315 |
330 |
345 |
e(ωt) |
-125 |
-139,3 |
-173 |
-194,6 |
-175 |
-104,8 |
0 |
104,8 |
РЕШЕНИЕ
Для разложения заданной несинусоидальной функции e(ωt) в гармонический ряд воспользуемся заданным в таблице разбиением ее на n=24 частей. Необходимые вычисления выполним в нижеприведенной таблице. Для этого просуммируем значения третьей, шестой, седьмой, двенадцатой и тринадцатой строк таблицы.
Сумма значений третьей строки равна нулю. Следовательно, постоянной составляющей в заданной несинусоидальной функции e(ωt) нет.
|
p |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
|||||||
1 |
ωt в гр. |
7,5 |
22,5 |
37,5 |
52,5 |
67,5 |
82,5 |
97,5 |
112,5 |
|
|||||||
2 |
ωt в рад. |
0,131 |
0,351 |
0,654 |
0,916 |
1,18 |
1,44 |
1,70 |
1,96 |
|
|||||||
3 |
e(ωt) |
175 |
192 |
156 |
130 |
130 |
156 |
187 |
190 |
|
|||||||
4 |
sin(ωt) |
0,130 |
0,343 |
0,608 |
0,793 |
0,924 |
0,991 |
0,991 |
0,924 |
|
|||||||
5 |
cos(ωt) |
0,991 |
0,939 |
0,793 |
0,609 |
0,383 |
0,131 |
-0,129 |
-0,382 |
|
|||||||
6 |
e(ωt)·sin(ωt) |
22,8 |
66,0 |
94,9 |
103 |
120 |
155 |
185 |
176 |
|
|||||||
7 |
e(ωt) ·cos(ωt) |
173,5 |
181 |
124 |
79,2 |
49,8 |
20,5 |
-24,2 |
-72,5 |
|
|||||||
8 |
3ωt в гр. |
22,5 |
67,5 |
112.5 |
158 |
202 |
248 |
293 |
338 |
|
|||||||
9 |
3ωt в рад. |
0,392 |
1,05 |
1,963 |
2,75 |
3,53 |
4,32 |
5,10 |
5,89 |
|
|||||||
10 |
sin(3ωt) |
0,382 |
0,868 |
0,924 |
0,384 |
-0,381 |
-0,923 |
-0,924 |
-0,385 |
|
|||||||
11 |
cos(3ωt) |
0,92 |
0,496 |
-0,382 |
-0,923 |
-0,924 |
-0,385 |
0,380 |
0,923 |
|
|||||||
12 |
e(ωt) ·sin(3ωt) |
66,9 |
167 |
144 |
49,9 |
-49,5 |
-144 |
-173 |
-73,2 |
|
|||||||
13 |
e(ωt) ·cos(3ωt) |
161,7 |
95,3 |
-59,6 |
-120 |
-120 |
-60,0 |
71,1 |
175 |
|
|||||||
|
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
|||||||||
ωt в гр. |
127,5 |
143 |
156 |
173 |
188 |
203 |
218 |
233 |
|||||||||
ωt в рад. |
2,22 |
2,48 |
2,75 |
3,01 |
3,27 |
3,53 |
3,79 |
4,06 |
|||||||||
e(ωt) |
146 |
54 |
-54 |
-146 |
-190 |
-187 |
-156 |
-130 |
|||||||||
sin(ωt) |
0,794 |
0,609 |
0,384 |
0,132 |
-0,129 |
-0,381 |
-0,607 |
-0,792 |
|||||||||
cos(ωt) |
-0,608 |
-0,793 |
-0,923 |
-0,991 |
-0,992 |
-0,925 |
-0,795 |
-0,610 |
|||||||||
e(ωt) ·sin(ωt) |
116 |
32,9 |
-20,7 |
-19,3 |
24,5 |
71,3 |
94,7 |
103 |
|||||||||
e(ωt) ·cos(ωt) |
-88,7 |
-42,8 |
49,9 |
145 |
188 |
173 |
124 |
79,4 |
|||||||||
3ωt в гр. |
383 |
428 |
473 |
518 |
563 |
608 |
653 |
698 |
|||||||||
3ωt в рад. |
6,67 |
7,46 |
8,24 |
9,03 |
9,81 |
10,6 |
11,4 |
12,2 |
|||||||||
sin(3ωt) |
0,379 |
0,922 |
0,925 |
0,387 |
-0,378 |
-0,922 |
-0,926 |
-0,388 |
|||||||||
cos(3ωt) |
0,925 |
0,386 |
-0,379 |
-0,922 |
-0,926 |
-0,388 |
0,377 |
0,921 |
|||||||||
e(ωt) ·sin(3ωt) |
55,4 |
49,8 |
-49,9 |
-56,5 |
71,8 |
172 |
144 |
50,5 |
|||||||||
e(ωt) ·cos(3ωt) |
135 |
20,9 |
20,5 |
135 |
176 |
72,5 |
-58,9 |
-120 |
|||||||||
p |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
ωt в гр. |
248 |
263 |
278 |
293 |
308 |
323 |
338 |
353 |
ωt в рад. |
4,32 |
4,58 |
4,84 |
5,10 |
5,36 |
5,63 |
5,89 |
6,15 |
e(ωt) |
-130 |
-156 |
-187 |
-190 |
-146 |
-54 |
54 |
146 |
sin(ωt) |
-0,923 |
-0,991 |
-0,992 |
-0,925 |
-0,795 |
-0,611 |
-0,385 |
-0,134 |
cos(ωt) |
-0,385 |
-0,133 |
0,128 |
0,380 |
0,607 |
0,792 |
0,923 |
0,991 |
e(ωt) ·sin(ωt) |
112 |
155 |
186 |
176 |
116 |
33,0 |
-20,8 |
-19,5 |
e(ωt) ·cos(ωt) |
50,0 |
20,7 |
-23,9 |
-72,3 |
-88,6 |
-42,7 |
49,8 |
145 |
3ωt в гр. |
743 |
787 |
833 |
878 |
923 |
968 |
101, |
1056 |
3ωt в рад. |
12,9 |
13,7 |
14,5 |
15,3 |
16,1 |
16,9 |
17,7 |
18,5 |
sin(3ωt) |
0,377 |
0,921 |
0,927 |
0,390 |
-0,375 |
-0,921 |
-0,927 |
-0,391 |
cos(3ωt) |
0,926 |
0,389 |
-0,376 |
-0,921 |
-0,927 |
-0,390 |
0,374 |
0,920 |
e(ωt) ·sin(3ωt) |
-49,0 |
-144 |
-173 |
-74,2 |
54,8 |
49,7 |
-50,1 |
-57,1 |
e(ωt) ·cos(3ωt) |
-120 |
-60,7 |
70,2 |
175 |
135 |
21,1 |
20,2 |
134 |
Используя выражения (4), (5), (6) и (7) определим амплитуду и начальный фазовый сдвиг первой и третьей гармоник ЭДС.
Синусная составляющая 1-ой гармоники:
![]()
Косинусная составляющая 1-ой гармоники:
![]()
Амплитуда ЭДС для первой гармоники:
![]()
Начальная фаза первой гармоники:
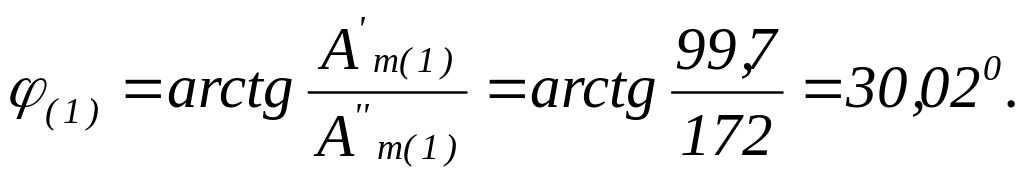
Синусная составляющая 3-ей гармоники:
![]()
Косинусная составляющая 3-ей гармоники:
![]()
Амплитуда ЭДС для третьей гармоники:
![]()
Начальная фаза третьей гармоники: