6. Разложение на симметричные составляющие.

а) Аналитический способ.

Токи нулевой последовательности:

Токи прямой последовательности:

А.

Тогда А;

А.

Токи обратной последовательности:

А;

А; А.

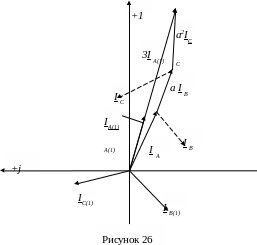
б) Графический способ.

Выберем масштаб токов m_i=2A/cm и выполним построения согласно уравнениям (1), (2), (3) (стр. 40).

Получение симметричных составляющих токов нулевой последовательности графическим способом с помощью уравнения (1) показано на рисунке 25.

Симметричные составляющие токов прямой и обратной последовательностей, полученные графически, приведены соответственно на рисунках 26 и 27.

Рисунок 27

МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ ПО ВЫПОЛНЕНИЮ

РАСЧЕТНОЙ РАБОТЫ № 4 на тему

Несинусоидальные токи в трехфазных цепях

Целью выполнения данной расчетной работы является получение навыка разложения несинусоидальной периодической функции времени в ряд Фурье, а также расчета разветвленных электрических цепей несинусоидального периодического тока с несколькими источниками ЭДС, в частности трехфазных цепей.

Согласно заданию необходимо рассчитать токи и напряжения на указанных участках трехфазной электрической цепи при наличии несинусоидальных ЭДС источника питания. вариант задания расчетной работы, выполняемой по данной теме, выбирается из приложения к данному учебному пособию либо выдается преподавателем. Каждый вариант отличатся от другого либо значениями исходных данных, либо схемой электрической цепи (ЭЦ).

Прежде, чем приступить к расчетам, необходимо изучить соответствующий раздел курса теоретических основ электротехники и ответить на контрольные вопросы.

Вопросы для самоконтроля

• Какой ток называют несинусоидальным?

• Как разложить несинусоидальную периодическую функцию времени в ряд Фурье?

• Каков порядок расчета цепи несинусоидального тока?

• Как определить действующее значение несинусоидального тока (напряжения)?

• Как вычислить мощность активную, реактивную, полную цепи несинусоидального тока?

• Как определить коэффициент мощности цепи несинусоидального тока?

• Для чего и каким образом необходимо учитывать систему электроизмерительного прибора при использовании его для измерений в цепях несинусоидального тока?

• Какими коэффициентами характеризуют несинусоидальные токи и напряжения?

Особенностью расчетов цепей несинусоидального тока является то, что студенту приходится решать последовательно как бы несколько однотипных задач. То есть рассчитывают частичные токи и напряжения на участках цепи, создаваемые постоянной составляющей несинусоидального напряжения (если она есть), и каждой из гармоник действующего напряжения в отдельности. При нахождении общего решения (действующих на участках цепи токов и напряжений), руководствуются принципом суперпозиции (наложения), справедливым для любой линейной электрической цепи, представляя полученный ток или напряжение в виде гармонического ряда вида:

где А₀ – постоянная составляющая или нулевая гармоника;

А_m(1) – амплитуда основной (первой) гармоники;

А_m(k) – амплитуда k-ой гармоники;

ω – основная частота;

ψ_(k) – начальная фаза k-ой гармоники.

Иначе, ряд Фурье можно представить в виде синусоид и косинусоид, каждая из которых имеет нулевую начальную фазу:

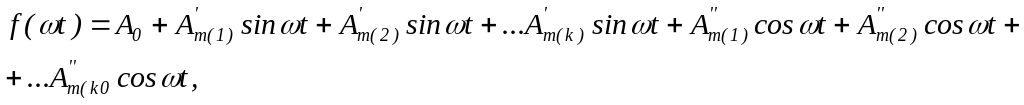где А’_m(1) – амплитуда синусной составляющей основной (первой)

гармоники и так далее;

А’’_m(1) – амплитуда косинусной составляющей основной (первой) гармоники и так далее.

Амплитуды постоянной, синусной и косинусной составляющих можно определить следующим образом:

Прежде чем начать расчет, необходимо несинусоидальную периодическую функцию времени, заданную в виде числового ряда, разложить в ряд Фурье, представленный выше. Для этого используют графический метод определения гармоник ряда Фурье, основанный на замене определенного интеграла суммой конечного числа слагаемых.

Принимают период заданной несинусоидальной периодической функции f(ωt) равным 2π. Разбивают период на n равных частей продолжительностью Δωt=2π/n. Измеряют, если функция f(ωt) задана графически, или вычисляют, если она задана таблично, ее значения f_q(ωt) в середине каждого полученного интервала Δωt_q, где q = 1, 2, 3, … , n – порядковый номер интервала Δωt. Вычисляют приближенные значения интегралов, заменяя их суммами:

;

; (4)

. (5)

Тогда значения амплитуд и начальную фазу соответствующих гармоник вычисляют, используя выражения:

(6)

и . (7)

При определении знака угла ψ_k (начальной фазы гармоники) нужно учитывать, какой знак имеют коэффициенты А’_m(k) и А’’_m(k).

Для определения числа и номера высших гармоник часто достаточно разбить исходную функцию f(ωt) на 15…24 части.

Для того, чтобы не делать лишней вычислительной работы полезно по рекомендуемым учебникам познакомиться с некоторыми свойствами несинусоидальных кривых, обладающих симметрией.

Действующее значение тока в k-ой ветви определяют по формуле:

,

где k – номер ветви (индекс тока);

n – порядковый номер гармоники тока;

I_k(n) – действующее значение тока n-ой гармоники в k-ой ветви.

,

где I_km(n) – амплитуда тока n-ой гармоники.

Аналогично рассчитывают действующее значение напряжения.

При определении показаний измерительных приборов необходимо учитывать систему электроизмерительного прибора (амперметра, вольтметра), поскольку приборы электромагнитной, электродинамической и тепловой систем измеряют действующее значение тока или напряжения на участке цепи. Приборы магнитоэлектрической системы показывают постоянную составляющую тока или напряжения, приборы с выпрямителями реагируют на среднее значение, а приборы индукционного типа – действующее значение только переменной составляющей. На максимальное значение периодической величины реагируют электронные амплитудные вольтметры.

Например, пусть в цепи, изображенной на рисунке 28, ток равен:

А.

Параметры цепи: R = 10 Ом; ωL= 20 Ом .

Измерительные приборы:

РА1 – электромагнитной системы;

PV1 – магнитоэлектрической системы, PV2 – электродинамической системы.

Тогда показания амперметра будут равны:

Для определения показаний вольтметра PV1 вычислим постоянную составляющую напряжения на активном сопротивлении, поскольку прибор магнитоэлектрической системы реагирует только на эту величину:

.

При определении показаний вольтметра PV2 электродинамической системы необходимо учитывать следующее. Поскольку Х_L= 0 на постоянном токе, то постоянная составляющая напряжения на индуктивности

комплекс напряжения первой гармоники на индуктивности

,

тогда мгновенное значение напряжения на индуктивности от первой гармоники тока

.

Комплекс напряжения на индуктивности, создаваемого третьей гармоникой тока:

Обратите внимание на то, что индуктивное сопротивление с увеличением номера гармоники возрастает пропорционально частоте. В случае наличия емкости на участке цепи, емкостное сопротивление участка с увеличением частоты будет уменьшаться в обратной пропорции.

Мгновенное напряжение на индуктивности от третьей гармоники тока

Тогда показания вольтметра PV2 будут равны:

Для определения полной активной мощности цепи вычисляют активные мощности, выделяемые на участке постоянной составляющей:

и каждой гармоникой в отдельности:

…………………………

Активная мощность цепи несинусоидального тока равна:

Реактивная мощность вычисляется также для каждой гармоники тока:

…………………………

Результирующая реактивная мощность цепи будет равна:

Полная мощность цепи определится по формуле:

,

где U и I – действующие значения напряжения и тока на данном участке

цепи.

Следует отметить, что при наличии несинусоидальных токов нельзя вычислять полную мощность цепи по формуле:

.

Коэффициент мощности цепи определится как

.

Коэффициент амплитуды k_a есть отношение максимального значения периодической функции к его действующему значению:

.

Например, для синусоиды .

Коэффициент формы k_ф есть отношение действующего значения периодической функции к его среднему значению:

,

например, для синусоиды

Коэффициент искажения k_И есть отношение действующего значения основной гармоники периодической функции к действующему значению самой функции:

,

для синусоиды