Пример выполнения расчетной работы № 3

Исходные данные:

Сопротивления:	Фазные и линейные напряжения:
Ом;	; В;
Ом;	В; ;
Ом.

П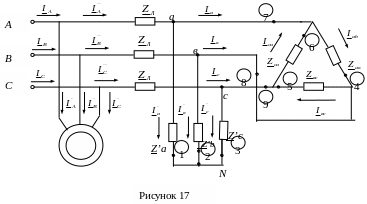 аспортные данные электродвигателя:U = 380\220 В; мощность на валу Р₂ =1,7 кВт; cos=0,86; КПД - 0,82. Заданная точка обрыва трехфазной цепи -5.

РЕШЕНИЕ

1. Выбираем схему соединения электродвигателя.

Обмотки двигателя следует соединить звездой, так как фазное напряжение сети соответствует напряжению на фазе двигателя.

Вычертим схему подключения потребителей (рисунок 17).

2. Определяем фазные и линейные токи потребителей и ток в начале линии.

Определим токи двигателя. Ток в фазе А:

.

Этот ток будет отставать по фазе от фазного напряжения на угол  = arccos(0,86) = 31⁰. Поэтому в комплексной форме этот ток и токи других фаз запишутся следующим образом:

;

;

.

Рассчитаем токи статической нагрузки. Так как статическая нагрузка представляет собой соединение сопротивлений звездой и треугольником, то следует преобразовать либо треугольник в эквивалентную звезду, либо звезду в эквивалентный треугольник. В данном случае можно использовать любой способ, так как и треугольник и звезда - симметричны.

П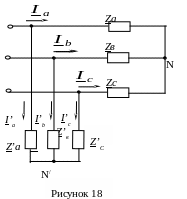 реобразуем треугольник в эквивалентную звезду (рисунок 18):

; Ом.

Потенциалы точек N^/ и N одинаковы, следовательно, две параллельные звезды можно объединить в одну, последовательно соединенную с сопротивлениями линии. Тогда схема электрической цепи примет вид, показанный на рисунке 19.

Сопротивление фазы

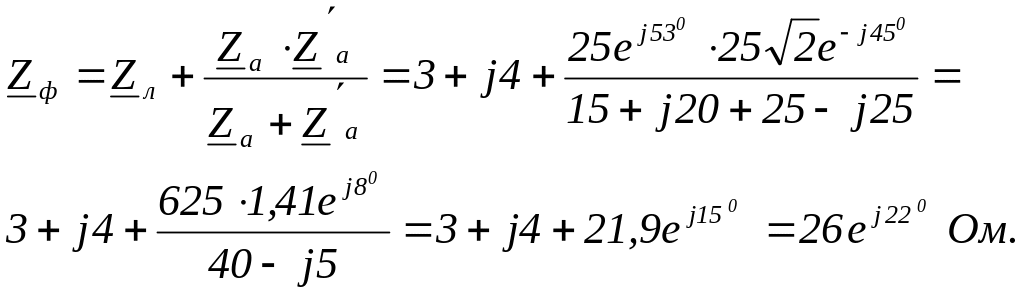
Определим токи , , . Эквивалентная схема статической нагрузки изображена на рисунке 20.

А;

А;

А .

Определяем фазные напряжения на нагрузке , , .

В;

В;

В.

Определим токи: , , .

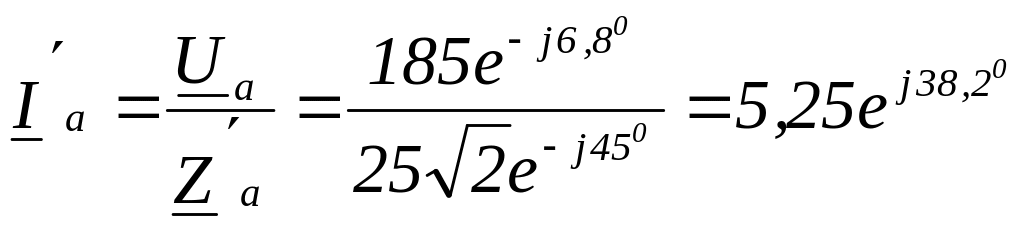А;

;

.

Определим токи , , , которые являются линейными токами треугольника нагрузки:

А;

;

.

Определим фазные токи треугольника , и . В симметричном треугольнике линейный ток больше фазного в раз и отстает от соответствующего фазного тока на угол 30⁰, то есть , отсюда:

A;

A;

A .

Определим токи в начале линии:

;

A;

A .

3. Определим КПД линии электропередачи. Поскольку электрическая цепь симметричная, КПД линии можно определить для одной фазы:

,

где Р_ф.н.— активная мощность в нагрузке, Вт;

Р_ф.— полная активная мощность фазы, Вт.

Вт;

Вт;

.

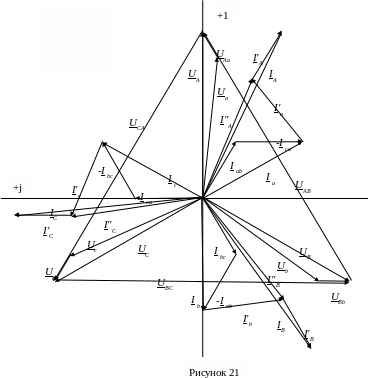
4. Топографическая диаграмма напряжений, совмещенная с векторной диаграммой токов, показана на рисунке 21. Для ее построения выбирают масштабы токов и напряжений.

5. Определить токи в начале линии при обрыве провода в точке (5) и разложить их аналитически и графически на симметричные составляющие.

С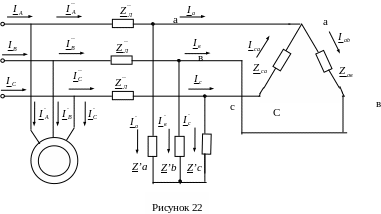 хема электрической цепи после обрыва представлена на рисунке 22.

Токи , , не зависят от изменения статической нагрузки и изменяться не будут. Ток , .

Для расчетов токов преобразуем звезду в эквивалентный треугольник

,

так как _ ; _;

Ом.

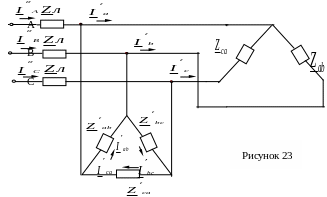
Полученная в результате преобразований схема электрической цепи показана на рисунке 23. Сопротивление включено параллельно сопротивлению , а сопротивление параллельно сопротивлению .

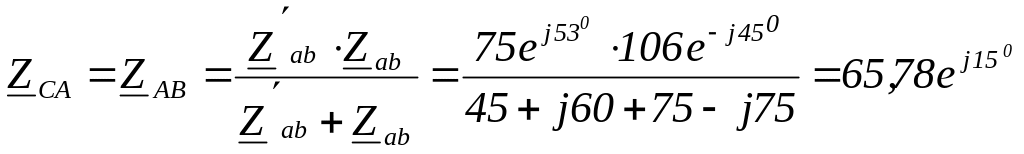
Ом, Ом.

П

реобразуем полученный треугольник в эквивалентную звезду сопротивлений:

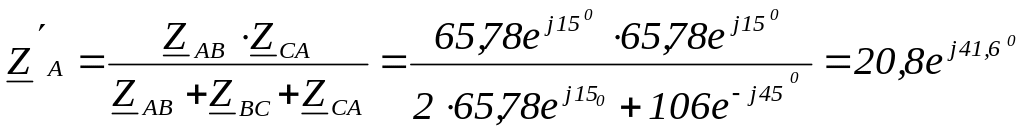Ом;

Ом;

Ом.

Упрощенная схема электрической цепи показана на рисунке 24. Определяем сопротивления и проводимости фаз :

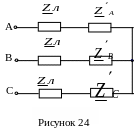
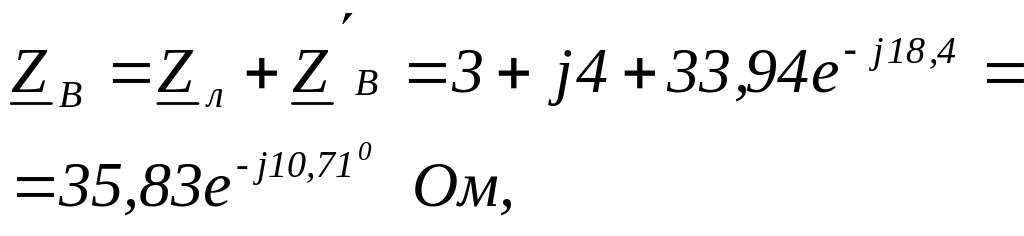
= Ом, Ом.

См; См.

Определяем токи ; ; .

А.

Аналогично рассчитаем:

=

А.

Итак, фазные токи:

А;

А; А .

А; А; А.