17)) Понятие о доверительных интервалов. Доверительный интервал для математического ожидания. Доверительный интервал для вероятности события.
17)) Продолжение
18))Проверка статистических гипотез. Критерии согласия «хи-квадрат».
Статистической гипотезой называется гипотеза, которая относится
к виду функции распределения, к параметрам функции распределения, к
числовым характеристикам случайной величины и т.д., и которую можно
проверить на основе опытных данных.
Критерий согласия Пирсона χ2 – один из основных, который можно представить как сумму отношений квадратов расхождений между теоретическими (fТ) и эмпирическими (f) частотами к теоретическим частотам:
k–число групп, на которые разбито эмпирическое распределение,
fi–наблюдаемая частота признака в i-й группе,
fT–теоретическая частота.
19))Проверка параметрических гипотез. Лемма Неймана-Пирсона.
Статистическая гипотеза называется параметрической, если в ней сформулированы предположения относительно значений параметров функции распределения известного вида.
Если
f(x1,x2,…,x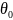n,
)
и f(x1,x2,…,xn,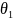
)взаимно
абсолютно непрерывны, то для любого
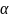(0 <
<1 ) можно указать такое С > 0 , что точки
выборочного пространства, в которых
!!!!!!!!!!!!!
образуют
критическую область Wo,
для которой Р(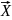
)
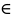Wo/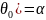
.
При этом Wo будет наиболее мощным критерием для проверки гипотезы Н0
против альтернативы Н1.
20)) Понятие о регрессивном анализе. Изучения корреляционной зависимости на основе опытных данных. Метод наименьших квадратов.
Регрессионным анализом называется раздел мат.
стат, объед. практические методы исследования
корреляц. зависимости между сл вел по
рез.
наблюдений над ними. Сюда включаются
методы выбора модели изучаемой зависимости
и оценки ее парам, методы проверки
статистич гипотез о зависимости. Изучения
корреляционной зависимости на основе
опытных данных. Пусть
из теоретических соображений или на
основе имеющихсяданных известно, что
уравнение линии регрессии имеет вид
y=f(a
a
,
где тип функции известен, но неизвестны
значения параметров a
.
.Проделаем
n
опытов,
в которых одновременно будем наблюдать
величины Х и Y. В результате наблюдений
получим n
пар
чисел (X
Это
и есть тот статистический материал, из
которого нужно извлечь информацию о
неизвестных значениях параметров. Как
уже было отмечено, линия регрессии
проходит так, что средний квадрат
отклонений Y от этой линии минимален,
сл-но, минимальна и сумма квадратов этих
отклонений. В этом состоит суть метода
наименьших квадратов. По рез наблюдений
мож найти не сами парам, а только их
оценки. Оценки парам находятся из условия
минимума ф-ии
F(a
.
Для
нахождения минимума приравняем к нулю
частные производные этой функции
Решаем
эту систему относит. a
.
В рез. получ оценки для неизв парам, а
затем и оценку самой линии регрессии.
Метод наименьш. квадратов (МНК) — мат метод, применяемый для реш различ задач, основанный на минимизации суммы квадратов некоторых функций от искомых переменных. Используется для «решения» переопределенных сист. ур. (когда к-во ур-ний превышает количество неизв), для поиска решения в случае обычных (не переопределенных) нелинейных систем уравнений, для аппроксимации точечных значений некоторой функцией. МНК является одним из базовых методов регрессионного анализа для оценки неизвестных параметров регрессионных моделей по выборочным данным.