1))Комбинаторика.Основной комбинаторный принцип.Сочетание,размещение,перестановка.Предмет теории вероятностей. Комбинато́рика — раздел математики, изучающий дискрет. объекты, мн-ва (сочетания, перестановки, размещ. и перечисления эл-тов) и отношения на них (напр., частичн. порядка)

Основной комбинаторный принцип. Если нек. 1ый выбор мож сделать t способами, для каждого 1ого выбора некоторый 2ой мож. сделать s способами, для кажд. пары 1ых 2ух – 3ий выбор мож. сдел. k спос.. и т.д., то число способов для послед-ти таких выборов = tsk ×××....

Размещениями множества из различн. эл-ов по эл-ов наз-ся комбинации, которые составлены из данных эл-ов по эл-ов и отличаются либо самими эл-ми, либо порядком элементов. Число всех размещений мн-ва из элементов по эл-ов обозначается через . Число размещений мн-ва из элементов по эл-ов равно

Перестановкой мн-ва из эл-ов наз-ся расположение эл-ов в опред. порядке. Перестановки можно считать частным случаем размещений при . Число всех перестановок из элементов обозначается . число всех различных перестановок вычисляется по формуле

Сочетаниями из различн. эл-ов по эл-ов наз-ся комбинации, которые сост. из данных эл-ов по эл-ов и отличаются хотя бы одним эл-ом. Обозначается .

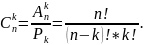
Предмет теории вероятностей

Теория вероятностей изучает закономерности, возникающие в случайных экспериментах. Случайным называют эксперимент, результат которого нельзя предсказать заранее.

2)) Статистическое и классическое определение вероятности. Свойства вероятностей.

Классическое определение вероятности. Если исходы опыта равновозможны,то вероятн. событ. A назыв-ся отношение числа исходов, благоприятств. данному событию , к числу всех возможных исходов опыта , т.е. P(A) = m/ n , где M – число исходов опыта , благоприятств. событ., а n – число всех возможн. исходов.

Статистическое определение вероятностей Относительной частотой событ. назыв. Отнош. числа испытаний, в котор. событ. появилось, к общему числу практически произведенных испытаний. Относительная частота А определяется формулой: w(A) = m/n, где m-число появлений события, n-общее число испытаний.

Свойства вероятностей. 1. Вероятность любого события – есть число , заключенное между нулем и единицей , т.е . 0 ≤ Р (А)≤ 1. Вероятность невозможного события равна 0, а вероятность достоверного события равна 1. 2. Если события A и B несовместны , то Р=( А+В) =Р(А)+Р(В). 3. Вероятность любого события A в сумме с вероятностью противо - положного события A( с черточкой вверху) равна единице : Р (А) + Р( А) с черточкой = 1. Если вероятн. интересующего нас событ. A по каким-либо причинам вычислить трудно, то можно попытаться вычислить вер. противоположного события, а затем с помощью св-ва 3 вычислить искомую вероятност события A.

3)) Условные вероятности. События зависимые и независимые. Теорема умножения вероятностей.

Условной вероятностью (два обозначения) называют вероятность события В, вычисленную в предположении, что событие А уже наступило.

Вероятность совместного появления двух зависимых событий равна произведению вероятности одного из них на условную вероятность второго, вычисленную при условии, что первое событие произошло, т.е. .

В частности, отсюда получаем .

События называются независимыми в совокупности, если любое из них не зависит от любого другого события и от любой комбинации остальных.

События называются зависимыми, если одно из них влияет на вер. появления другого. Напр., 2 производственные установки связаны единым технологическим циклом. Тогда вер. выхода из строя 1ой из них зависит от того, в каком состоянии находится др. Условие независимости событ. от событ. записывают в виде , а условие его зависимости — в виде .

Теорема умножения вероятностей.

Вер. произведения событ. равна вер. 1ого событ., умноженной на вер. другого событ., вычисленную при условии, что 1ое событ. произошло, т.е.

P(AB)=P(A)P(B/A)=P(B)P(A/B)

События назыв. независимыми, если появление 1ого из них не изменяет вер. появления другого. Если событ. независимы, то P(A/B)=P(A), P(B/A)=P(B) и P(AB)=P(A)P(B). Для любого конечного числа событий вер. произведения событ равна произведению вер. этих событ, причем вер. каждого след. событ. вычисляется при условии, что

пред. события произошли, т.е.

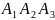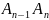P(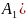 *…* )=P( P(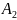 / 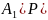)*…*P(An/A1A2A3*…*An-1).

Если события независимы, то

P(A1A2A3*…*An-1An) = P(A1)P(A2)P(A3)*…*P(An)

Перед вычислением вер. произведения событ.

необх.о установить, зависимы события или нет.