Методические указания для проведения практических занятий

В данных указаниях даются необходимые теоретические сведения, формулы, методические рекомендации, решения типичных задач и варианты заданий контрольной работы для студентов заочной формы обучения.

Рассмотрены следующие темы: исследование экономических задач методами дифференциального исчисления; изучение экономических систем с помощью линейных балансовых моделей, сетевое планирование и управление, исследование эластичности производственных функций, элементы линейного программирования и матричных игр и т.д.

Содержание

Введение……………………………………………………………………………...3

1. Тема 1. Исследование функций в экономике методами дифференциального исчисления……………………………………………………………………………4

2. Тема 2. Линейные балансовые модели…………………………………………..7

3.Метод множителей Лагранжа……………………………………………………..9

4. Линейное программирование. Симплексный метод……………………………13

5.Транспортная задача линейного программирования………………………...20

6. Парная регрессия и корреляция. Аппроксимация функций……………………31

7.Приложения теории графов……………………………………………………….35

Введение

Методические указания посвящены решению простейших задач экономики математическими методами: исследование экономических функций методами дифференциального исчисления, в частности, эластичностью; изучение экономических систем на основе линейных балансовых моделей, симплекс методом в линейном программировании, транспортной задачи, теории игр и т.д.

1. Исследование функций в экономике методом дифференциального исчисления

Приведем некоторые необходимые для решения задач понятия и формулы дифференциального исчисления в экономике ([1], [3]).

Пусть – количество произведенной продукции за время t. Производительность труда есть производная объема произведенной продукции.

Отношение , т.е. фактически производная логарифмической функции называется темпом изменения функции.

Поясним понятие предельных издержек. Пусть х – объем производства некоторой продукции, – производственная функция, описывающая зависимость издержек производства (суммарные затраты) от объема производства. Тогда предел

,

равный производной выражает предельные издержки производства и характеризует приблизительно дополнительные затраты на производство единицы дополнительной продукции.

Определение. Удельные затраты – это средние затраты на единицу продукции, т.е.

.

Задача 1. Объем продукции рабочего описывается уравнением

, ,

где t – рабочее время в часах. Вычислить производительность труда, скорость и темп её изменения через 1 час после начала работы и за 2 часа до конца рабочего дня.

Решение. Производительность труда равняется производной от объема продукции, :

.

Скорость изменения производительности труда равен производной от производительности труда:

.

Темп изменения производительности труда равен , т.е. фактически :

.

Вычисляем эти показатели при :

, ;

, ;

, .

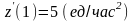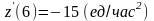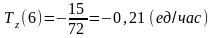Вывод: к концу работы производительность труда снижается, причем смена знака 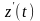и к концу рабочего дня на «минус» свидетельствует, что увеличение производительности в начале рабочего дня сменяется её снижением в конце рабочего дня.

Задача 2. Зависимость спроса товара от цены выражается формулой

.

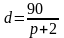Найти предельный спрос при цене: ,

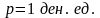Решение. Скорость изменения функции равна её производной, здесь

Отсюда , .

Знак «минус» показывает, что с увеличением цены спрос на товар падает.

Темп изменения равен

при , при .

Задача 3. Найдите предельную производительность ресурса, если функция выпуска имеет вид , а затраты ресурса равны:

1. 2 усл. ед.

2. 5 усл. ед.

Определите, начиная с какого момента увеличение затрат экономически невыгодно.

Решение. Производительность равна 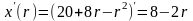. При , при .

Здесь с увеличением затрат ресурса производительность падает. Причем при , т.е. при увеличение затрат экономически невыгодно.

Задача 4. Пусть издержки производства вычисляются по формуле

.

1. Определить предельные издержки при .

2. При каких значениях х издержки производства возрастают все медленнее; всё быстрее?

3. При каком объеме производства х удельные затраты будут минимальными?

Решение.

1. Предельные издержки равны

.

Здесь

2. Далее, , здесь при и при 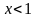. То есть если выпуск продукции меньше 1 усл. ед., то издержки производства возрастают всё медленнее. Если , то издержки растут всё быстрее.

3. Удельные затраты (К_ср) равны

.

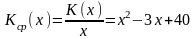Далее, , 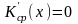при – это точка минимума (почему?) К_ср(х).

Задача 5. Функция спроса от цены имеет вид

.

Постройте график функции. Определите при каких р спрос эластичен, нейтрален, неэластичен.

Решение. Эластичность вычисляется по формуле:

,

а для функции спроса

, ,

,

.

Здесь спрос эластичен: при .

Спрос нейтрален: при .

Спрос неэластичен: при .

Вывод: при увеличении цены больше спрос эластичен, т.е. товар меньше востребован.