8. Контрольные задания

Студенты очной формы обучения выполняют в течение семестра три контрольные работы. Распределение контрольных работ в семестре устанавливается графиком учебного процесса. Студентами очной формы обучения предлагаемые ниже задания могут быть использованы для самостоятельной работы и для самоконтроля при подготовке к контрольным работам.

Студенты заочной формы обучения выполняют одну контрольную работу. К зачету допускаются студенты, у которых зачтена контрольная работа. Каждый студент заочного отделения для своего варианта контрольной работы выбирает из списка задач те, номера которых оканчиваются на ту же цифру, что и номер его зачетки. Эта цифра и является номером его варианта.

Правила оформления контрольных работ:

При выполнении контрольных работ следует придерживаться указанных ниже правил. Работы, выполненные без соблюдения этих правил, могут быть не зачтены и возвращены студенту для переработки.

1. Каждую контрольную работу следует выполнять в отдельной тетради чернилами любого цвета, кроме красного, оставляя поля для замечаний рецензента.

2. На обложке тетради должны быть ясно написаны фамилия, имя, отчество студента, название дисциплины, номер варианта, специальность и группа, в которой обучается студент. Здесь указываются фамилия, имя, отчество рецензента. В конце работы следует проставить дату выполнения и расписаться.

3. В работу включаются все задачи строго по положенному варианту. Работа, содержащая не все задачи варианта или задачи не своего варианта, не зачитывается.

4. Решение задач надо располагать в порядке номеров, указанных в задании, сохраняя номера задач. Решение задач излагать подробно и аккуратно, объясняя все действия.

5. Если работа не зачтена или сделаны замечания по решению задач, следует выполнить работу над ошибками в той же тетради. В связи с этим рекомендуется при выполнении контрольной работы оставлять в конце тетради несколько чистых листов для всех исправлений и дополнений в соответствии с указаниями рецензента. Вносить исправления в сам текст работы после ее рецензирования запрещается.

Задание 1.

1. Рассчитать эффективную ставку сложных процентов, если номинальная равна 58% годовых и начисление процентов происходит ежемесячно.

2. Найти текущее значение инвестиций при ежемесячном начислении процентов по ставке сложного процента – 9% годовых, если наращенная к концу 7-го года сумма должна составлять 756 345 д.ед.

3. Какой выигрыш получит инвестор за 5 лет от инвестирования 500 000 д.ед. по ставке сложного процента 7,25% годовых, если вместо ежегодного будет использовать непрерывное наращивание.

4. Найти текущее значение инвестиций, если наращенная к концу 5-го года сумма при поквартальном начислении по ставке сложного процента 9% годовых, составит 562 387 д.ед.

5. Предприятие получило заем на два года в размере 10 млн. руб. с условием вернуть 16 млн. руб. Рассчитайте процентную и учетную ставки (простые проценты).

6. Пусть современная стоимость $1000, которые мистер А получит по банковскому депозиту через 2 года при постоянной интенсивности , равна удвоенной современной стоимости $600, которые мистер В получит по депозиту через 4 года при том же . Найти .

7. Пусть счет с начальной суммой 100 д.ед. при годовой ставке простого процента 20% годовых открывается в момент времени 0. Спустя год открывается счет с начальной суммой 110 д.ед. с той же ставкой. Найти момент времени, когда накопленные суммы обоих счетах сравняются.

8. Вексель номиналом 1 000 д.ед. куплен по цене 850 д.ед. за 90 дней до погашения. Найти соответствующие учетную и процентную ставки (простые проценты) сделки.

9. Пусть кредитор выдал 14 февраля кредит на сумму 600 000 д.ед. под 10% годовых (простые проценты). Дата погашения кредита 27 августа. Найти сумму процентов и сумму погашения кредита.

10. Вкладчик за 2 года накопил при простой ставке 20% годовых 210 д.ед. На сколько увеличится вклад за следующие 3 года.

Задание 2.

1. Определить под какую ставку процентов выгоднее поместить капитал в 10 млн. д.ед. на пять лет: а) под простую 90% годовых; б) под сложную 49% годовых.

2. Найти срок ссуды в 350 000 руб. при наращивании по номинальной ставке 7,5% годовых поквартально до 550 000 руб.

3. Какова продолжительность займа (в годах) размером 115 000$, выросшего до 151 000$ по ставке простого процента 6% годовых.

4. Найти наращенную сумму на ссуду в 112 500 руб. с 1 марта по 12 сентября при условии, что проценты начисляются по простой учетной ставке 8,7% годовых.

5. На счете в банке 1,2 млн. руб. Банк платит 12,5% годовых (сложные проценты). Предлагается войти всем капиталом в совместное предприятие, при этом прогнозируется удвоение капитала через 5 лет. Принимать ли это предложение?

6. Был оформлен заем на следующих условиях: в первые 4 месяца установлена простая процентная ставка 8,5% годовых, в следующие 3 месяца происходит увеличение процентной ставки на 0,5%. Найти сумму первоначального займа, если сумма возврата составляет 28 915,38 руб.

7. Определить процентную ставку и современную стоимость пятилетнего платежа в 5 000 руб. при условии, что дисконтирование производится по силе роста 12% годовых.

8. Множитель наращения за два года составил 1,15, при этом на втором году начисления ставка сложного процента увеличилась на 1%. Определить исходную величину ставки сложного процента.

9. Найти номинальную ставку с ежемесячной капитализацией, эквивалентную эффективной ставке 8,75% в год.

10. Пусть банк выплачивал проценты (сложные) по накопительным вкладам в размере 10% годовых в течение 1-го года, 15% – в течение 2-го года, и 8% – в течение 3-го года. Каков размер вклада в конце последнего года, если исходная его величина составляла 30 000 руб.

Задание 3.

1. На какой срок нужно поместить 100 000 д.ед. под сложные годовые проценты – 25%, чтобы накопить к концу срока 350 000 д.ед.

2. Необходимо определить значение учетной ставки эквивалентной простой 12%.

3. Найти учетную ставку эквивалентную эффективной сложной процентной ставке 12% годовых для двухгодичного периода.

4. Какова первоначальная сумма ссуды сроком на 200 дней, если через 90 дней она была учтена по простой учетной ставке 6,55% годовых и была получена сумма 52 300 д.ед.

5. Пусть 10% – месячная ставка начисления, 3,31% – квартальная. Являются ли эквивалентными эти ставки?

6. Начальная величина вклада составляет 200 д.ед. Период начисления процентов 1 мес. Найти накопленную сумму и сложные проценты за 5 лет и 3 месяца, если месячная ставка начисления по вкладу 3%.

7. Пусть 9,5% – номинальная годовая процентная ставка с ежеквартальным начислением. Найти эффективную годовую процентную ставку эквивалентную данной.

8. Найти накопленное значение суммы 300 д.ед. за 4 года, если номинальная годовая ставка 10%, период начисления 6 мес.

9. Определить множитель наращения за 3 года при силе роста 10% годовых (ответ округлить до сотых).

10. Пусть по годовой шкале задана номинальная непрерывно начисляемая ставка 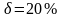. Найти накопленное по этой ставке за 3,5 года значение суммы 500 д.ед.

Задание 4.

1. В контракте два платежа S₁ = 140 000 руб. со сроком 35 дней и S₂ = 50 000 руб. со сроком 120 дней заменяются одним в 100 дней. При консолидации применяется ставка годового сложного процента 11%. Найти новую сумму.

2. Два платежа заменяются одним в 550 000 д.ед. со сроком 210 дней по ставке простого процента 7,5% годовых. Найти величину первого платежа со сроком 180 дней, если 2-ой величиной 350 000 д.ед. имеет срок 220 дней.

3. Пусть в момент времени 0 выдан заем на сумму 5 000 д.ед. сроком на два года, по истечении которых кредитор должен получить 10 000 д.ед. Найти ставку простого процента этой сделки.

4. Найти срок ссуды в 35 000 д.ед. при наращивании по номинальной ставке 7% годовых поквартально до 55 000 д.ед.

5. Два платежа заменяются одним в 400 000 д.ед. со сроком 180 дней по сложной процентной ставке 7% годовых. Найти величину первого платежа со сроком 200 дней, если 2-ой величиной 150 000 д.ед. со сроком 150 дней.

6. Платежи в 1 000$ и 2 000$ со сроками уплаты 2 и 3 года соответственно объединяются в один платеж со сроком 2,5 года. При консолидации используется сложная ставка 20%. Найти сумму консолидированного платежа.

7. Пусть инвестор ежегодно вносит в банк на пополняемый счет 300 д.ед. Банк платит 10% годовых. Какова будет сумма вклада через 5 лет, если инвестор вносит очередной вклад в конце каждого года.

8. Долг 150 350 д.ед. взят на 5 лет. Определить величину срочной уплаты после 2-го года в схеме погашения долго равными суммами, если применяется процентная ставка 12% годовых.

9. Размер взноса в погасительный фонд составляет 1 500 д.ед., какова сумма долга, если процентная ставка в погасительном фонде 11,25% годовых, а срок – 2,1 года.

10. Определить эффективную ставку сложных процентов с тем, чтобы получить такую же наращенную сумму, как и при использовании номинальной годовой ставки 6% при ежемесячном начислении.

Задание 5.

1. Определить срок действия аннуитета постнумерандо, если коэффициент приведения аннуитета пренумерандо 4,45, годовая процентная ставка – 12%.

2. Аннуитет постнумерандо с первым платежом 250 д.ед. действует 4 года, годовая процентная ставка равна 9%. Какова величина увеличения платежа, если наращенная сумма составляет 2 344,16 д.ед.

3. Суммы в размере 100 тыс., 30 тыс. и 10 тыс. руб. должны быть выплачены через 15, 6 и 3 месяца соответственно. Стороны согласились заменить их одним платежом сроком на год и простой ставкой 12% годовых. Определить размер консолидированной суммы.

4. Два платежа 45 тыс. и 78 тыс. руб. со сроками 4 и 9 месяцев соответственно консолидированы в общий платеж 130 тыс. с годовым сроком. Какова простая ставка процента консолидации?

5. Долг в сумме 10 000 руб. необходимо погасить последовательными равными срочными уплатами за 5 лет платежами постнумерандо. За заем выплачиваются проценты по ставке 5% годовых. Составьте план амортизации займа.

6. Какова величина второго платежа аннуитета постнумерандо, если каждый следующий платеж увеличивается в 3 раза, процентная ставка – 15% годовых, срок действия аннуитета 4 года, современная стоимость аннуитета составляет 400 000 руб.

7. Кредит в размере 30 млн. руб., выданный под 50% годовых, должен погашаться равными суммами в течение 5 лет. Определить размеры ежегодных срочных уплат и сумму выплаченных процентов, если погасительные платежи осуществляются один раз в конце года.

8. Имеются два обязательства 500 д.ед. и 690 д.ед. с соответствующими сроками 35 и 48 дней. Начало отсчета срока приходится на один день. Можно ли считать их равноценными, если используется простая процентная ставка 15% годовых.

9. Кредит на сумму 10 млн. руб. с ежегодным начислением сложных процентов по ставке, равной 20% годовых, должен погашаться в течение 5 лет равными срочными уплатами. Определить размер срочной уплаты.

10. Пусть инвестор ежегодно вносит в банк на пополняемый счет 300 д.ед. Банк платит 10% годовых. Какова будет сумма вклада через 5 лет, если инвестор вносит очередной вклад в начале каждого года.

Задание 6.

1. По данным о доходности 3-х активов рассчитать корреляционную матрицу.

   Доходность	1 период	2 период	3 период
   A	0,01	0,01	0,05
   B	0,03	0,06	0,06
   C	0,01	-0,02	0,02

2. Дана корреляционная матрица и риск 2-х акций соответственно: 0,12, 0,2. Найти риск портфеля, состоящего из этих акций, если в нем 16% акций 1-го вида и 84% – второго.

3. По данным о доходности 3-х активов рассчитать корреляционную матрицу, вектор средней доходности.

   Доходность	1 период	2 период	3 период
   A	0,01	0,03	0,05
   B	0,04	0,06	0,08
   C	0,03	-0,02	0,02

4. По данным о доходности 3-х активов рассчитать корреляционную матрицу, вектор средней доходности.

   Доходность	1 период	2 период	3 период
   A	0,04	0,05	0,09
   B	0,07	0,065	0,12
   C	-0,02	0,04	0,07

5. По данным о доходности 3-х активов рассчитать ковариационную матрицу.

   Доходность	1 период	2 период	3 период
   A	0	0,03	0,05
   B	-0,01	0,01	0,03
   C	0,03	0,01	0,01

6. Портфель инвестора включает акции 2-х компаний А и В. Характеристика возможных ставок доходности и вероятность их достижения приведены в таблице. Определить во сколько раз акции одной компании рискованней акций другой.

   Вероятность	Доходность
   	А	В
   0,1	60%	-10%
   0,35	40%	5%
   0,55	15%	30%

7. Дана ковариационная матрица доходности 3-х активов 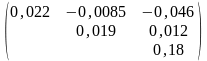. Найти корреляционную матрицу и сделать вывод.

8. Дана корреляционная матрица 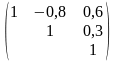и риск 3-х акций соответственно: 0,11, 0,1, 0,13. Найти риск портфеля, состоящего из этих 3-х акций, если в нем 10% акций 1-го вида, 25% – второго и 65% – третьего.

9. Можно ли найти структуру безрискового портфеля, составленного из 2-х активов с характеристиками , , .

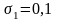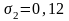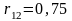10. По данным о доходности 3-х активов рассчитать корреляционную матрицу.

Доходность	1 период	2 период	3 период
A	0,01	-0,01	0,05
B	0,01	0	0,06
C	0,02	-0,02	0,02