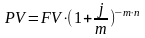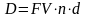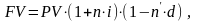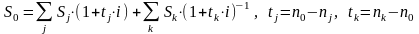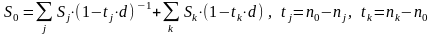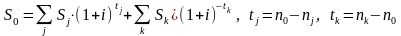3. Дисконтирование

Процесс дисконтирования в определенном смысле является обратным по отношению к процессу начисления процентов. Например, в кредитном секторе под дисконтированием понимают авансовое удержание с заемщика процентов в момент выдачи ссуды, то есть до наступления срока ее погашения. В финансовой практике существуют два вида дисконтирования: математическое дисконтирование и банковский учет.

1. При математическом дисконтировании по заданной сумме FV, которая образуется через некоторое время n, необходимо определить первоначальную сумму PV. В этом случае говорят, что сумма FV дисконтируется. Величину PV, найденную дисконтированием наращенной суммы FV, называют современной стоимостью. С помощью дисконтирования в финансовых операциях учитывается фактор времени. Разность FV-PV можно рассматривать не только как проценты, начисленные на PV, но и как дисконт с суммы FV: D=FV-PV. Дисконтирование по простым процентам осуществляется по формуле (3.1), а для сложных процентов – (3.2-3.3):

		(3.1)
	,	(3.2) (3.3)

2. Банковский учет представляет собой учет векселей, суть которого в том, что банк до наступления срока платежа по векселю покупает его у владельца по цене меньшей той суммы, которая должна быть выплачена по нему в конце срока, т.е. приобретает или учитывает его с дисконтом, при этом применяется учетная ставка d. Преобразуя формулу (1.3), получим формулу (3.4), отражающую процесс дисконтирования по удержанию:

		(3.4)
		(3.5)

В отдельных случаях может возникнуть ситуация, когда совмещают начисление процентов по ставке i и дисконтирование по ставке d. В этом случае наращенная величина ссуды будет определяться по формуле (3.6):

(3.6)

где n – общий срок платежного обязательства в годах; n' – срок от момента учета обязательства до даты погашения долга в годах, то есть n' < n.

Задачи для самостоятельного решения:

1. Какова сумма дисконта при продаже финансового инструмента на сумму 5 000 руб., если срок его погашения 2,5 года. Покупатель применил сложную годовую учетную ставку 8% годовых.

2. В условия задачи 2.8 найти дисконт по сложной учетной ставке 4 раза в год.

3. Обязательство 20 000 руб. должно быть погашено через 5 лет, учетная ставка 5% годовых, начисление дисконта поквартальное. Найти современную величину обязательства и эффективную учетную ставку.

4. Найти наращенную сумму долга 10 000 руб., если срок погашения 1,5 года и в контракте предусмотрена сложная годовая учетная ставка 10%.

5. Какова эффективность выраженная в годовой сложной ставке, дисконтирования векселя по простой ставке 8% годовых через 120 дней.

4. Консолидация задолженностей

Пусть платежи , отсчитываемые от одной базы со сроками 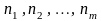объединяются на основе простых процентов в один платеж 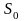с новым сроком 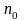, тогда величина консолидированного платежа будет рассчитываться по формуле (4.1):

(4.1)

При объединении платежей на основе учетной ставки и сложной процентной ставки, для расчета величины консолидированного платежа будут действовать формулы (4.2) и (4.3) соответственно:

		(4.2)
		(4.3)

Задачи для самостоятельного решения:

1. Платежи S₁ = 100 000 руб. и S₂ = 50 000 руб. со сроками n₁ = 150 дней и n₂ = 180 дней, отсчитываемые от одной базы, заменяются одним со сроком в 200 дней. Найти величину консолидированного платежа при использовании ставки простого процента равной 6% годовых..

2. Два векселя со сроками 10 июня стоимостью 10 000 руб. и 1 августа – 20 000 руб. заменяются одним с продлением срока до 1 октября. Определить размер суммы нового векселя, если при объединении применена учетная ставка 8% годовых.

3. Платежи S₁ =100 000 руб. и S₂ = 50 000 руб. со сроками n₁ = 150 дней и n₂ = 180 дней, отсчитываемые от одной базы, заменяются одним со сроком в 200 дней. Найти величину консолидированного платежа, если была использована сложная годовая ставка 6% годовых.

4. Платежи в размере 10 000, 20 000, 15 000 руб. уплачиваются через 50, 80 и 150 дней после некоторой даты. Решено заменить их одни платежом 50 000 руб. Найти срок консолидированного платежа, при условии, что i = 10%.

5. Решить предыдущую задачу, при условии, что размер консолидированного платежа равен сумме объединяемых обязательств.

6. Два обязательства в сумме 100 000 руб. и 50 000 руб. должны быть погашены соответственно 1-го ноября и 1-го января следующего года. Стороны согласились пересмотреть условие так, что должник 10-го декабря уплачивает 60 000 руб., а остальной долг гасится 1-го марта. Найти сумму нового платежа, при условии, что применяется простая ставка процентов 6%.
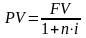
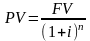