ВОЛЖСКИЙ ГУМАНИТАРНЫЙ ИНСТИТУТ

(ФИЛИАЛ)

федерального государственного автономного образовательного учреждения высшего профессионального образования

«ВОЛГОГРАДСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ»

Е.А. Решетняк, Н.С. Талалаева

Сборник задач по дисциплине «Финансовая математика»

для студентов направления подготовки бакалавров «Экономика»

очной и заочной форм обучения

Аннотация

Сборник задач предназначен для студентов высших учебных заведений очной и заочной форм обучения по направлению подготовки бакалавров 080100 «Экономика», а также слушателей системы переподготовки по специальности «Финансы и кредит», преподавателей и всех интересующихся финансовыми расчетами. Решение представленных задач позволяет овладеть навыками применения аппарата финансовой математики для расчетов простых и сложных процентов (выдача ссуды, продажа товара в кредит, помещение средств на депозитный счет, учет векселя, потоки платежей и т. д.), анализировать и осмысливать практические финансовые задачи, систематизировать свои знания в этой области.

Содержание

Введение 4

1. Простые проценты 5

2. Сложные проценты 8

3. Дисконтирование 10

4. Консолидация задолженностей 12

5. Аннуитеты 13

6. Варианты погашения задолженности 19

7. Риск и доходность активов. Элементы теории портфеля 22

8. Контрольные задания 26

Список литературы 35

Введение

Сборник задач – учебное издание, содержащее задачи способствующие усвоению теоретического материала в рамках практической части дисциплины «Финансовая математика», целью которой является изучение и усвоение студентами теоретических основ и практических навыков проведения с применением математического аппарата количественного анализа некоторых финансовых операций (накопление и дисконтирование по простым и сложным процентам, финансовые ренты, формирование портфеля ценных бумаг и т.п.), в том числе с использованием ППП Excel.

Сборник содержит следующие разделы: простые проценты; сложные проценты; дисконтирование; консолидация задолженностей; аннуитеты; варианты погашения задолженности; риск и доходность активов, элементы теории портфеля, при этом в начале каждого раздела приводятся основные расчетные формулы. В разделе «Контрольные задания» систематизированы задачи, которые будут полезны для студентов очной формы обучения при закреплении пройденного материала по соответствующей теме. Для студентов заочной формы обучения контрольная работа формируется из шести задач – по одной из каждого Задания 1 – 6.

Решение предложенных в сборнике задач позволит учащимся освоить практику проведения финансово-экономических расчетов и использования современных методов финансовых вычислений в экономических исследованиях, банковской практике, инвестиционных проектах, при планировании производственных и коммерческих операций организаций и т.д.

1. Простые проценты

Проценты (процентные деньги) – это абсолютная величина дохода от предоставления капитала в долг в любой ее форме (выдача ссуды, покупка облигации, учет векселя, продажа товара в кредит и т.д.) либо от инвестиций производственного или финансового характера.

Величина получаемого дохода определяется исходя из величины вкладываемого капитала, срока, на который предоставляется в долг или инвестируется капитал, размера и вида процентной ставки.

Наращение основной суммы FV происходит за счет присоединения процентных денег к основному капиталу, при этом множителем (коэффициентом) наращения называется безразмерная величина, которая показывает во сколько раз вырос капитал.

Существует два способа начисления процентов: декурсивный и антисипативный (таблица 1.1). При обоих способах проценты могут быть либо простыми, либо сложными.

Таблица 1.1 – Характеристика декурсивного и антисипативного способов начисления процентов

Характеристики	Декурсивный способ	Антисипативный способ
Начисление процентов	В конце каждого интервала начисления	В начале каждого интервала начисления
Величина процентов	Определяется исходя из величины PV	Определяется исходя из величины FV
Процентная ставка	Отношение суммы начисленного за определенный интервал дохода (процентов) к сумме имеющегося капитала на начало данного интервала	Отношение суммы дохода, выплачиваемой за определенный интервал, к величине наращенной суммы – учетная процентная ставка

На практике применяются три варианта расчета процентов с использованием временной базы T:

1. Точные проценты с точным число дней («английская практика»): Т = 365 (366) дней. Точное число дней t определяется путем подсчета числа дней между датой выдачи ссуды (инвестирования) и датой ее погашения (окончания срока инвестирования).

2. Обыкновенные (коммерческие) проценты с точным числом дней («французская практика»): Т = 365 дней. Величина t рассчитывается как в предыдущем случае.

3. Обыкновенные проценты с приближенным числом дней («германская практика»). В этом случае год делится на 12 месяцев, по 30 дней в каждом и Т = 360 дней.

Простые процентные ставки обычно применяются:

• в краткосрочных финансовых операциях, когда интервал начисления совпадает с периодом начисления (и составляет, как правило, срок менее одного года), или когда после каждого интервала начисления кредитору выплачиваются проценты;

• при определении доходности ценных бумаг.

При декурсивном способе начислении простых процентов наращенная сумма определяется по формуле (1.1):

, ,

(1.1)

где FV – наращенная сумма, д. ед.;

PV – величина первоначальной денежной суммы, д. ед.;

i – годовая ставка простого процента, %;

n – продолжительность периода начисления в годах: ;

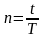t – продолжительность периода начисления в днях (месяцах);

Т – временная база – количество дней (месяцев) в году;

I – сумма процентных денег за весь период начисления, д. ед..

Если процентная ставка изменяется во времени, то наращенная сумма примет вид (1.2):

,

(1.2)

где i_t – ставка простого процента, установленная на период n_t, %.

При антисипативном способе начислении процентов наращенная сумма имеет вид (1.3):

, ,

(1.3)

где d – простая годовая учетная процентная ставка, %;

n – продолжительность периода времени от даты погашения до даты учета в годах.

На практике учетные ставки применяются главным образом при учете (т.е. покупке) векселей и других денежных обязательств, при этом временная база (Т) принимается в 360 дней. Дисконтом (D) называется доход, полученный по учетной ставке, т.е. разница между размером кредита и непосредственно выдаваемой суммой.

Задачи для самостоятельного решения:

1. Определить сумму накопленного долга и процентный платеж, если размер ссуды равен 7 000 руб., срок долга 4 года при ставке простого процента 10% годовых.

2. Ссуда в 100 000 руб. выдана 20 января до 5 октября под 8% годовых, T = 365 дней. Найти размер погасительного платежа.

3. По контракту в 1-ый год начисляется 6% годовых, в каждом следующем полугодии ставка повышается на 0,5%. Определить множитель наращения за 2,5 года.

4. Через 180 дней с момента подписания контракта должник уплатит 31 000 руб. Кредит предоставлен под 6% годовых. Определить какую сумму получил должник и сумму дисконта. T = 365 дней.

5. Тратта (переводной вексель) выдана на 100 000 руб. с уплатой 17 ноября. Владелец векселя учел его в банке 23 сентября по учетной ставке 8% годовых без учета комиссионных. Найти РV и D.

6. Найти наращенную сумму на ссуду в 100 000 руб., выданную 20 января сроком до 5 октября при условии, что проценты начисляются по простой годовой учетной ставке 8%.

7. Какова должна быть продолжительность ссуды в днях, для того, чтобы долг равный 10 000 руб. вырос до 10 500 руб., при условии, что на сумму долга начисляются простые проценты по ставке 28% годовых. T = 365 дней.

8. В контракте предусмотрено погашение обязательства через 120 дней в сумме 12 000 руб. Первоначальная сумма составляет 11 500 руб. Необходимо определить доходность операции для кредитора в виде учетной и процентной ставки.
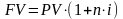