Метод замены переменной

Метод интегрирования подстановкой заключается во введении новой переменной интегрирования (то есть подстановки). При этом заданный интеграл приводится к новому интегралу, который является табличным или к нему сводящимся. Пусть требуется вычислить интеграл   Сделаем подстановку   где   — функция, имеющая непрерывную производную.

Тогда   и на основании свойства инвариантности формулы интегрирования неопределенного интеграла получаем формулу интегрирования подстановкой:

Интегрирование по частям — применение следующей формулы для интегрирования:

Или:

В частности, с помощью n-кратного применения этой формулы находится интеграл

где   — многочлен  -ой степени.

32 определен.интеграл и его определение

Определённым интегралом от функции   на отрезке  называется предел интегральных сумм при стремлении ранга разбиения к нулю  , если он существует независимо от разбиения   и выбора точек  , то есть

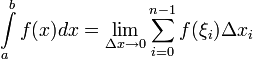
Если существует указанный предел, то функция   называется интегрируемой на   по Риману.

Формула Ньютона — Лейбница или основная теорема анализа даёт соотношение между двумя операциями: взятием определённого интеграла и вычислением первообразной.

Если   непрерывна на отрезке   и 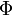  — её любая первообразная на этом отрезке, то имеет место равенство

33 Комплекс.числа.формы записи

Ко́мпле́ксные числа — числа вида  , где   и   — вещественные числа,   — мнимая единица; то есть  . Множество всех комплексных чисел обычно обозначается 

Формы записи

• Алгебраическая форма

Запись комплексного числа   в виде  , где   и  , называется алгебраической формой комплексного числа.

• Тригонометрическая форма

Если вещественную   и мнимую   части комплексного числа выразить через модуль   и аргумент   ( ,  ), то всякое комплексное число  , кроме нуля, можно записать в тригонометрической форме

• Показательная форма

Применяя формулу Эйлера к тригонометрической форме, получим показательную форму комплексного числа:

где   — расширение экспоненты для случая комплексного показателя степени.

Отсюда вытекают следующие широко используемые равенства:

34 простейш.операции над Комплек.числ

Действия над комплексными числами

• Сравнение

 означает, что   и   (два комплексных числа равны между собой тогда и только тогда, когда равны их действительные и мнимые части).

• Сложение

• Вычитание

• Умножение

• Деление

• В частности,

35диффер.урав. осн понятия

Дифференциальным уравнением называется уравнение, связывающее независимую переменную  , искомую функцию   и её производные  , т. е. уравнение вида

Порядком дифференциального уравнения называется порядок наивысшей производной, входящей в уравнение. Например, дифференциальное уравнение   — уравнение первого порядка, дифференциальное уравнение  , где   — известная функция, — уравнение второго порядка; дифференциальное уравнение   — уравнение 9-го порядка.

Дифференциальные уравнения с разделяющимися переменными  .

Прежде чем продолжить, напомним, что   когда y является функцией аргумента x.

В дифференциальных уравнениях   или   переменные могут быть разделены, проведением преобразований. Такие ОДУ называются дифференциальными уравнениями с разделяющимися переменными. Соответствующее ДУ с разделенными переменными запишется как  .

36 линейные.диффер.уравн

Линейным дифференциальным уравнением первого порядка называется уравнение, линейное относительно неизвестной функции и её производной. Оно имеет вид

(1)

где   и   — заданные функции от  , непрерывные в той области, в которой требуется проинтегрировать уравнение (1).

Если  , то уравнение (1) называется линейным однородным. Оно является уравнением с разделяющимися переменными и имеет общее решение

Общее решение неоднородного уравнения можно найти методом вариации произвольной постоянной, который состоит в том, что решение уравнения (1) ищется в виде

, где   — новая неизвестная функция от  .

37 решение.линейн.однород.уравнений

Общее решение линейного однородного дифференциального уравнения   с непрерывными на интервале интегрирования Xкоэффициентами   определяется линейной комбинацией 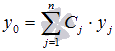 , где   - линейно независимые частные решения ЛОДУ на X, а   - произвольные постоянные.

Таким образом, общее решение линейного однородного дифференциального уравнения второго порядка   с постоянными коэффициентами имеет вид y₀=C₁⋅y₁+C₂⋅y₂, где y₁ и y₂ – частные линейно независимые решения, а С₁ и C₂ – произвольные постоянные. Осталось научиться находить частные решения y₁ и y₂.

Эйлер предложил искать частные решения в виде  .

Если принять   частным решением ЛОДУ второго порядка с постоянными коэффициентами  , то при подстановке этого решения в уравнение мы должны получить тождество:

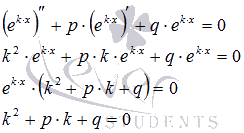
Ab altero expectes, alteri quod feceris.