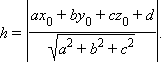Durov.all rights reserved.
Матрицей A=Amn порядка m*n называется прямоугольная таблица чисел, содержащая m - строк и n - столбцов.
Элементы матрицы aij, у которых i=j, называются диагональными и образуют главную диагональ.
Для квадратной матрицы (m=n) главную диагональ образуют элементы a11, a22,..., ann .
Действия над матрицами.
1. Сложение матриц - поэлементная операция
2. Вычитание матриц - поэлементная операция
3. Произведение матрицы на число - поэлементная операция
4. Умножение A*B матриц по правилу строка на столбец (число столбцов матрицы А должно быть равно
числу строк
матрицы B)
5![]() .
Возведение в степень
.
Возведение в степень
m>1 целое положительное число. А - квадратная матрица (m=n) т.е. актуально только
для квадратных матриц
6. Транспонирование матрицы А. Транспонированную матрицу обозначают AT или A'
Свойства опрераций над матрицами
A+B=B+A
(A+B)+C=A+(B+C)
λ(A+B)=λA+λB
A(B+C)=AB+AC
(A+B)C=AC+BC
λ(AB)=(λA)B=A(λB)
A(BC)=(AB)C
(A')'=A
(λA)'=λ(A)'
(A+B)'=A'+B'
(AB)'=B'A'
Определи́тель (или детермина́нт) — одно из основных понятий линейной алгебры. Это многочлен, комбинирующий элементы квадратной матрицы таким образом, что его значение сохраняется при транспонировании и линейных комбинациях строк или столбцов.
СВОЙСТВО 1. Величина определителя не изменится, если все его строки заменить
столбцами, причем каждую строку заменить столбцом с тем же номером, то есть
СВОЙСТВО 2. Перестановка двух столбцов или двух строк определителя
равносильна умножению его на -1. Например,
СВОЙСТВО 3. Если определитель имеет два одинаковых столбца
или две одинаковые строки, то он равен нулю.
СВОЙСТВО 4. Умножение всех элементов одного столбца
или одной строки определителя на любое число k равносильно
умножению определителя на это число k. Например,
.СВОЙСТВО 5. Если все элементы некоторого столбца или некоторой строки равны нулю, то сам определитель равен нулю. Это свойство есть частный случае предыдущего (при k=0).
СВОЙСТВО 6. Если соответствующие элементы двух столбцов или двух строк определителя пропорциональны, то определитель равен нулю.
СВОЙСТВО 7. Если каждый элемент n-го столбца или n-й строки определителя представляет собой сумму двух слагаемых, то определитель может быть представлен в виде суммы двух определителей, из которых один в n-м столбце или соответственно в n-й строке имеет первые из упомянутых слагаемых, а другой - вторые; элементы, стоящие на остальных местах, у вех трех определителей одни и те же. Например,
СВОЙСТВО 8. Если к элементам некоторого столбца (или некоторой строки) прибавить соответствующие элементы другого столбца (или другой строки), умноженные на любой общий множитель, то величина определителя при этом не изменится. Например,
.СВОЙСТВО 9. Определитель равен сумме произведений элементов какого-либо столбца (или строки) на их алгебраические дополнения.
О![]() бра́тная
ма́трица —
такая матрица A−1,
при умножении на которую, исходная
матрица A даёт
в результате единичную
матрицу E:
бра́тная
ма́трица —
такая матрица A−1,
при умножении на которую, исходная
матрица A даёт
в результате единичную
матрицу E:
Свойства обратной матрицы
![]() ,
где
,
где ![]() обозначает определитель.
обозначает определитель.
![]() для
любых двух обратимых матриц
для
любых двух обратимых матриц ![]() и
и ![]() .
.
![]() где
где ![]() обозначает
транспонированную матрицу.
обозначает
транспонированную матрицу.
![]() для
любого коэффициента
для
любого коэффициента ![]() .
Первый
способ.
.
Первый
способ.
1. Вычислить
определитель ![]() данной
матрицы. Если
данной
матрицы. Если ![]() ,
то обратной матрицы не существует
(матрица
,
то обратной матрицы не существует
(матрица ![]() вырожденная).
вырожденная).
2. Составить
матрицу ![]() из
алгебраических дополнений
из
алгебраических дополнений ![]() элементов
матрицы
3. Транспонируя
матрицу
,
получить присоединенную матрицу
элементов
матрицы
3. Транспонируя
матрицу
,
получить присоединенную матрицу ![]() .
.
4. Найти
обратную матрицу (4.1), разделив все
элементы присоединенной матрицы на
определитель ![]()
![]()
Второй способ. Для нахождения обратной матрицы можно использовать элементарные преобразования.(метод гаусса)
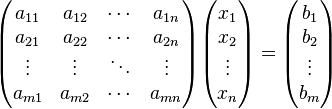
Системы линейных уравнений.метод крамера
Система m линейных алгебраических уравнений с n неизвестными (или, линейная система)
Здесь ![]() —
количество уравнений, а
—
количество уравнений, а ![]() —
количество неизвестных. x1, x2,
…, xn —
неизвестные, которые надо определить. a11, a12,
…, amn —
коэффициенты системы — и b1, b2,
… bm —
свободные члены — предполагаются
известными[1].
Индексы коэффициентов (aij)
системы обозначают номера уравнения
(i)
и неизвестного (j),
при котором стоит этот коэффициент,
соответственно.
Система
линейных уравнений может быть
представлена в
матричной форме как:
—
количество неизвестных. x1, x2,
…, xn —
неизвестные, которые надо определить. a11, a12,
…, amn —
коэффициенты системы — и b1, b2,
… bm —
свободные члены — предполагаются
известными[1].
Индексы коэффициентов (aij)
системы обозначают номера уравнения
(i)
и неизвестного (j),
при котором стоит этот коэффициент,
соответственно.
Система
линейных уравнений может быть
представлена в
матричной форме как:
Здесь
—
это матрица системы, ![]() —
столбец неизвестных, а
—
столбец неизвестных, а ![]() —
столбец свободных членов. Если к
матрице
приписать
справа столбец свободных членов, то
получившаяся матрица называется
расширенной.
—
столбец свободных членов. Если к
матрице
приписать
справа столбец свободных членов, то
получившаяся матрица называется
расширенной.
Метод Крамера
Система линейных уравнений:

Определители:

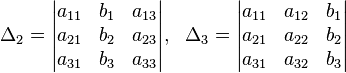
Решение:
![]()
5 Метод гаусса системы Уравнений.
Метод Гаусса –портрет Гаусса красовался на купюре в 10 дойчмарок (до введения евро), и до сих пор Гаусс загадочно улыбается немцам с обычных почтовых марок.
Сначала немного систематизируем знания о системах линейных уравнений. Система линейных уравнений может:
1) Иметь единственное решение. 2) Иметь бесконечно много решений. 3) Не иметь решений (быть несовместной).
Существуют следующие элементарные преобразования:
1) Строки матрицы можно переставлять местами.
2) Если в матрице есть (или появились) пропорциональные (как частный случай – одинаковые) строки, то следует удалить из матрицы все эти строки кроме одной.
3) Если в матрице в ходе преобразований появилась нулевая строка, то ее также следует удалить. Рисовать не буду, понятно, нулевая строка – это строка, в которой одни нули.
4) Строку матрицы можно умножить (разделить) на любое число, отличное от нуля. Рассмотрим
5) К строке матрицы можно прибавить другую строку, умноженную на число, отличное от нуля.
5 метод гаусса
метод гаусса состотит из двух основных этапов называемых прямым ходом и обратным ходом.
Суть прямого хода заключается в последовательном исключении неизвестных с целью преобразования системы к ступенчатому виду когда основная матрица системы имеет на главной диагонали отличные от нуля элементы а под главной диагональю находится только нулевые элемменты.
|
Обратный ход начинаетс с записи системы которой соответствует итоговая расширенная матрица полученная в результате прямого хода

Метод Гаусса является одним из самых наглядных и простых способов решения систем линейных алгебраических уравнений (СЛАУ): как однородных, так и неоднородных. Коротко говоря, суть этого метода состоит в последовательном исключении неизвестных.
6 вектор. Сложение умножение
Вектор – направленный отрезок прямой в плоскости либо в пространстве.
Нулевой вектор – любая точка на плоскости либо в пространстве.
Сложение
векторов ![]() и
и ![]() происходит
так: от произвольной точки A откладывается
вектор
происходит
так: от произвольной точки A откладывается
вектор ![]() ,
равный
,
далее от точки B откладываеься
вектор
,
равный
,
далее от точки B откладываеься
вектор ![]() ,
равный
,
и вектор
,
равный
,
и вектор ![]() представляет
собой сумму
векторов
и
.
Такой способ сложения двух векторов
называется правилом
треугольника.
представляет
собой сумму
векторов
и
.
Такой способ сложения двух векторов
называется правилом
треугольника.
Умножение
вектора на число k соответствует
растяжению вектора в k раз
при k > 1 или
сжатию в ![]() раз
при 0 < k < 1,
при k = 1 вектор
остается прежним (для отрицательных k еще
изменяется направление на противоположное).
Если произвольный вектор умножить на
ноль, то получим нулевой вектор.
Произведение нулевого вектора и
произвольного числа есть нулевой вектор.
раз
при 0 < k < 1,
при k = 1 вектор
остается прежним (для отрицательных k еще
изменяется направление на противоположное).
Если произвольный вектор умножить на
ноль, то получим нулевой вектор.
Произведение нулевого вектора и
произвольного числа есть нулевой вектор.
7. скаляр. Произведение векторов.
Скалярным произведением двух векторов называется действительное число, равное произведению длин умножаемых векторов на косинус угла между ними.
Скалярное
произведение векторов ![]() и
и ![]() будем
обозначать как
будем
обозначать как ![]() .
Тогда формула
для вычисления скалярного произведения имеет
вид
.
Тогда формула
для вычисления скалярного произведения имеет
вид ![]() ,
где
,
где ![]() и
и ![]() -
длины векторов
и
соответственно,
а
-
длины векторов
и
соответственно,
а ![]() -
угол между векторами
и
.
Из определения скалярного произведения
видно, что если хотя бы один из умножаемых
векторов нулевой, то .
-
угол между векторами
и
.
Из определения скалярного произведения
видно, что если хотя бы один из умножаемых
векторов нулевой, то .
Скалярным произведением двух векторов на плоскости или в трехмерном пространстве в прямоугольной системе координат называется сумма произведений соответствующих координат векторов a и b.
Т![]()
![]() о
есть, для векторов
на
плоскости в прямоугольной
декартовой системе координат формула
для вычисления скалярного произведения имеет
вид
о
есть, для векторов
на
плоскости в прямоугольной
декартовой системе координат формула
для вычисления скалярного произведения имеет
вид
![]()
![]() а
для векторов
в
трехмерном пространстве скалярное
произведение в координатах находится
как
а
для векторов
в
трехмерном пространстве скалярное
произведение в координатах находится
как
скалярным произведением двух не нулевых векторов называется число равное произведению длин этих векторов на косинус угла между ними.
Свойства.
свойство коммутативности скалярного произведения
 ;
;свойство дистрибутивности
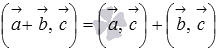 или
или 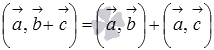 ;
;сочетательное свойство
 или
или 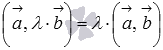 ,
где
,
где  -
произвольное действительное число;
-
произвольное действительное число;скалярный квадрат вектора всегда не отрицателен
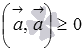 ,
причем
,
причем 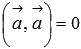 тогда
и только тогда, когда вектор
нулевой.
тогда
и только тогда, когда вектор
нулевой.
8 Векторное произведение векторов и его св-ва.
Векторным
произведением двух векторов ![]() и
и ![]() ,
заданных в прямоугольной системе
координат трехмерного пространства,
называется такой вектор
,
заданных в прямоугольной системе
координат трехмерного пространства,
называется такой вектор ![]() ,
что
,
что
он является нулевым, если векторы и коллинеарны;
он перпендикулярен и вектору и вектору (
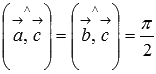 );
);его длина равна произведению длин векторов и на синус угла между ними (
 );
);тройка векторов
 ориентирована
так же, как и заданная система координат.
ориентирована
так же, как и заданная система координат.
В прямоугольной системе координат
трехмерного пространства векторное
произведение есть определитель квадратной
матрицы где
первая строка которой есть орты
прямоугольной системе координат
трехмерного пространства векторное
произведение есть определитель квадратной
матрицы где
первая строка которой есть орты ![]() ,
во второй строке находятся координаты
вектора
,
а в третьей –
координаты
вектора
в
заданной прямоугольной системе
координат:
,
,
во второй строке находятся координаты
вектора
,
а в третьей –
координаты
вектора
в
заданной прямоугольной системе
координат:
,
антикоммутативность
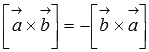 ;
;свойство дистрибутивности
 или
или 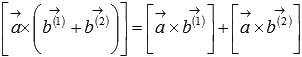 ;
;сочетательное свойство
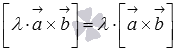 или
или 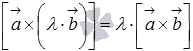 ,
где
,
где 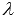 -
произвольное действительное число.
-
произвольное действительное число.
9 Смешанное произв. Вектр.и его св-ва
С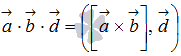 мешанным
произведением трех векторов
мешанным
произведением трех векторов ![]() и
и ![]() называется
действительное число, равное скалярному
произведению векторов
называется
действительное число, равное скалярному
произведению векторов  и
,
где
-
векторное
произведение векторов
и
.
и
,
где
-
векторное
произведение векторов
и
.
Векторное произведение в координатах имеет вид

а скалярное произведение векторов в прямоугольной системе координат равно
сумме произведений соответствующих координат, поэтому

свойства смешанного произведения:
 ;
;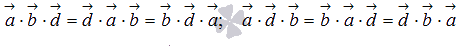 ;
;

Очевидно, что если хотя бы один из умножаемых векторов нулевой, то смешанное произведение равно нулю.
Смешанное произведение также равно нулю, если хотя бы два умножаемых вектора равны.
10 Условия колинеарности,компл и ортогонал.
Два ненулевых вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Нулевой вектор считается коллинеарным любому другому вектору.
Два
ненулевых вектора ![]() и
и ![]() коллинеарны
тогда и только тогда, когда их векторное
произведение равно нулевому вектору.
коллинеарны
тогда и только тогда, когда их векторное
произведение равно нулевому вектору.
Векторы называются компланарными, если они принадлежат одной или параллельным плоскостям.
Для
компланарности трех векторов ![]() и
и ![]() трехмерного
пространства необходимо и достаточно,
чтобы их смешанное произведение равнялось
нулю.
трехмерного
пространства необходимо и достаточно,
чтобы их смешанное произведение равнялось
нулю.
Два
ненулевых вектора называются перпендикулярными,
если угол между ними равен девяноста
градусам (![]() радиан).
радиан).
Для
перпендикулярности двух ненулевых
векторов
и
необходимо
и достаточно, чтобы их скалярное
произведение равнялось нулю, то есть,
чтобы выполнялось равенство

необходимое
и достаточное условие перпендикулярности
двух векторов в
координатах
имеет вид ![]() на
плоскости, а в трехмерном пространстве
на
плоскости, а в трехмерном пространстве ![]() .
.
11 Уравнение плоскости в Пространстве
Общее уравнение плоскости в декартовой системе координат записывается следующим образом:
ax + by + cz + d = 0. |
Если известно, что плоскость проходит через точку с координатами (x0, y0, z0), то ее уравнение можно привести к виду
a (x – x0) + b (y – y0) + c (z – z0) = 0. |
Уравнение
|
называется уравнением плоскости в отрезках на осях.
Нормаль
к плоскости имеет координаты ![]()
Угол между двумя плоскостями легко вычисляется по формуле скалярного произведения. Если эти плоскости задаются уравнениями a1x + b1y + c1z + d1 = 0 и a2x + b2y + c2z + d2 = 0, то угол между плоскостями равняется
|
Расстояние от точки (x0; y0; z0) до плоскости, задаваемой уравнением ax + by + cz + d = 0, равно
|
12 Уравнения прямой в пространстве
Векторное параметрическое уравнение прямой в пространстве:
![]()
где ![]() — радиус-вектор некоторой
фиксированной точки
— радиус-вектор некоторой
фиксированной точки ![]() лежащей
на прямой,
лежащей
на прямой, ![]() —
ненулевой вектор, коллинеарный этой
прямой (называемый её направляющим
вектором),
—
ненулевой вектор, коллинеарный этой
прямой (называемый её направляющим
вектором), ![]() — радиус-вектор произвольной
точки прямой.
— радиус-вектор произвольной
точки прямой.
Параметрические уравнения прямой в пространстве:
![]()
где ![]() — координаты некоторой
фиксированной точки
лежащей
на прямой;
— координаты некоторой
фиксированной точки
лежащей
на прямой; ![]() — координаты
вектора, коллинеарного этой
прямой.
— координаты
вектора, коллинеарного этой
прямой.
Каноническое уравнение прямой в пространстве:
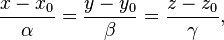
где — координаты некоторой фиксированной точки лежащей на прямой; — координаты вектора, коллинеарного этой прямой.
Общее векторное уравнение прямой[в пространстве:
Поскольку прямая является пересечением двух различных непараллельных плоскостей, заданных соответственно общими уравнениями:
![]() и
и ![]()
то уравнение прямой можно задать системой этих уравнений:

Векторное уравнение прямой в пространстве
Уравнение прямой в пространстве можно записать в виде векторного произведения радиуса-вектора произвольной точки этой прямой на фиксированный направляющий вектор прямой :
![]()
где
фиксированный вектор ![]() ,
ортогональный вектору
,
можно найти, подставляя в это уравнение
радиус-вектор какой-нибудь одной
известной точки прямой.
,
ортогональный вектору
,
можно найти, подставляя в это уравнение
радиус-вектор какой-нибудь одной
известной точки прямой.
13 Предел функции и его геометр.смысл. свойства.
Число А называется пределом функции в точке хо (или при х→хо), если для любого положительного ε найдется такое положительное число δ, что для все ххо, удовлетворяющих неравенству |х-хо|<δ, выполняется неравенство |ƒ(х)-А|<ε.

Геометрический смысл предела функции:
![]()
если для любой ε-окрестности точки А найдется такая δ-окрестность точки хо, что для всех ххо из етой δ-окрестность соответствующие значения функции ƒ(х) лежат в ε-окрестности точки А. Иными словами, точки графика функции у=ƒ(х) лежат внутри полосы шириной 2ε, ограниченной прямыми у=А+ ε , у=А-ε (см. рис. 110). Очевидно, что величина δ зависит от выбора ε, поэтому пишут δ=δ(ε).

14 Различные виды пределов.
Односторонние пределы.
Число
![]() называется пределом
функции
называется пределом
функции
![]() в
точке
в
точке
![]() слева или левосторонним
пределом,
если для любого, сколь угодно малого,
положительного
слева или левосторонним
пределом,
если для любого, сколь угодно малого,
положительного
![]() найдется
такое
найдется
такое
![]() ,
что для всех
,
что для всех
![]() таких,
что
таких,
что
![]() ,
выполняется неравенство
,
выполняется неравенство
![]() Предел
слева функции обозначается так:
Предел
слева функции обозначается так:
![]() или
или
![]()
Пределы на бесконечности.
Число
называется пределом
функции
при
![]() ,
если для любого, сколь угодно малого,
положительного
найдется
такое
,
если для любого, сколь угодно малого,
положительного
найдется
такое
![]() ,
что для всех
,
что для всех
![]() выполняется
неравенство
Пишем:
выполняется
неравенство
Пишем:
![]()
Бесконечные пределы.
Пусть
функция
неограниченно
возрастает в левосторонней окрестности
точки
.
Говорят, что функция стремится к
![]() ,
когда
,
когда
![]()
![]()
если
для любого, сколь угодно большого
числа
найденся
такое
,
что для всех
таких,
что
,
выполняется неравенство
![]() .
.
15 Бесконечно малые функции и св-ва
Функции ![]() и
и ![]() называют бесконечно
малыми при
называют бесконечно
малыми при ![]() ,
если
,
если ![]() и
и ![]()
Свойства.
1.
Если функции ![]() и
и ![]() являются
бесконечно малыми, то функция
являются
бесконечно малыми, то функция ![]() также
есть бесконечно малая. Это свойство
распространяется на случай алгебраической
суммы любого конечного числа бесконечно
малых.
также
есть бесконечно малая. Это свойство
распространяется на случай алгебраической
суммы любого конечного числа бесконечно
малых.
2.
Произведение ограниченной при ![]() функции
на бесконечно малую есть функция
бесконечно малая.
функции
на бесконечно малую есть функция
бесконечно малая.
3. Произведение постоянной на бесконечно малую есть бесконечно малая.
4. Произведение двух бесконечно малых есть бесконечно малая. Это свойство распространяется на любое конечное число бесконечно малых.
Теорема о связи между бесконечно большой и бесконечно малой функциями:
Если
функция ![]() -
функция бесконечно малая (
-
функция бесконечно малая (![]() ),
то функция
),
то функция ![]() есть
бесконечно большая функция и наоборот.
есть
бесконечно большая функция и наоборот.
Доказательство:
Пусть
-
бесконечно малая функция при ![]() ,
т.е.
,
т.е. ![]() .
Тогда для любого числа
.
Тогда для любого числа ![]() существует
такое число
существует
такое число ![]() ,
что для всех
,
что для всех ![]() ,
удовлетворяющих неравенству
,
удовлетворяющих неравенству ![]() ,
выполняется неравенство
,
выполняется неравенство ![]() ,
т.е.
,
т.е.![]() ,
т.е.
,
т.е. ![]() ,
где
,
где ![]() .
А из этого следует, что функция
.
А из этого следует, что функция ![]() -
бесконечно большая
-
бесконечно большая
16 Эквивалентно беск.мал.Замечател.пределы
Функции
и
называют эквивалентными
бесконечно малыми при
,
если 
Очень удобно пользоваться заменой эквивалентных бесконечно малых при нахождении пределов. Замена производится на основе таблицы.
Таблица эквивалентных бесконечно малых.
Пусть - бесконечно малая при .

З амеча́тельные
преде́лы —
термин, использующийся в советских и
российских учебниках по математическому
анализу для
обозначения некоторых широко
известных математических
тождеств со
взятием предела.
Особенно известны:
амеча́тельные
преде́лы —
термин, использующийся в советских и
российских учебниках по математическому
анализу для
обозначения некоторых широко
известных математических
тождеств со
взятием предела.
Особенно известны:
Первый замечательный предел:
Второй замечательный предел:

Функция у = f (х)
называется непрерывной
в точке ![]() ,
если бесконечно малому приращению
Δ х аргумента
х в точке
соответствует
бесконечно малое приращение функции
Δ y,
т. е.
,
если бесконечно малому приращению
Δ х аргумента
х в точке
соответствует
бесконечно малое приращение функции
Δ y,
т. е.  .
Другими словами, функция у = f (х)
непрерывна в точке
,
если
.
Другими словами, функция у = f (х)
непрерывна в точке
,
если
![]() ,
т. е. предел функции в точке
равен
значению функции в этой точке.
,
т. е. предел функции в точке
равен
значению функции в этой точке.
Непрерывность функции
На практике удобно использовать следующие 3 условия непрерывности функции f (x) в точке x = a :
Функция f (x) определена в точке x = a;
Предел
 существует;
существует;Выполняется равенство
 .
.
Определение непрерывности по Коши
Р![]()
![]() ассмотрим
функцию f (x),
которая отображает множество действительных
чисел
ассмотрим
функцию f (x),
которая отображает множество действительных
чисел ![]() на
другое подмножествоB действительных
чисел. Говорят, что
функция f (x) является непрерывной в
точке
на
другое подмножествоB действительных
чисел. Говорят, что
функция f (x) является непрерывной в
точке ![]() ,
если для любого числа
,
если для любого числа ![]() существует
число
существует
число ![]() ,
такое, что для всех
,
такое, что для всех ![]() ,
удовлетворяющих соотношению
,
удовлетворяющих соотношению
выполняется неравенство
Точка ![]() называется точкой
разрыва функции
называется точкой
разрыва функции ![]() ,
если она определена в некоторой проколотой
окрестности точки
(то
есть определена на некотором интервале,
для которого
служит
внутренней точкой, но в самой точке
,
возможно, не определена
,
если она определена в некоторой проколотой
окрестности точки
(то
есть определена на некотором интервале,
для которого
служит
внутренней точкой, но в самой точке
,
возможно, не определена