Пример решения задачи по теме 2.2 Силы давления

Определить силу давления воды на щит, перекрывающий треугольный водослив, если уровень воды 1,2 м, а угол при вершине 90°. Определить точку приложения силы давления.

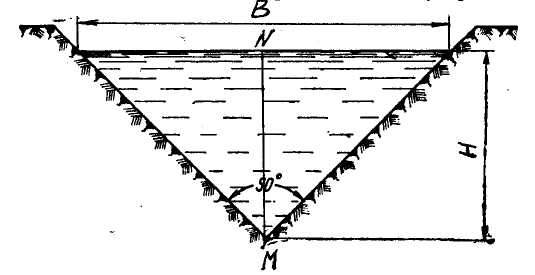
Рисунок 2.2 – Схема водослива

Дано	СИ
Н = 1,2 м	Н = 1,2 м
α = 90°	α = 90°
R = ?	R = ?

Решение

Полная результирующая сила давления жидкости на плоскую стенку равна произведению результирующего давления в центре тяжести стенки на смоченную площадь стенки.

R = (р₀ + ρ·g·h_С) ·F, Н,

где р₀ – давление на свободную поверхность жидкости, Па;

ρ – плотность жидкости, кг/м³;

g – ускорение свободного падения, g = 9,81 м/с²;

h_С – глубина погружения центра тяжести щита под свободной поверхностью жидкости, м;

F – смоченная площадь щита, м².

Так как давление на свободную поверхность жидкости и внешнее давление на стенку равны атмосферному, то сила давления на стенку равна

R = ρ·g·h_С ·F, Н

Плотность воды при температуре 20°C ρ = 998 кг/м³ ([2], стр.11, табл.1.3).

Глубина погружения центра тяжести треугольного щита, который представляет собой равнобедренный треугольник, h_С = Н/3 ([9], стр.42-43, табл.10)

Площадь щита

F = В·H/2, м²,

где В – основание щита, м;

Н – высота щита, м.

Для нахождения основания В проводится перпендикуляр МN на основание. Щит делится на два прямоугольных равнобедренных треугольника. Очевидно, что В/2 = Н, а В = 2·H. Тогда

F= Н², м²

Таким образом,

R = ρ·g·Н/3·Н² = ρ·g·Н³/3 = 998·9,81·1,2³/3 = 5639,26 Н

Глубина погружения центра давления щита (точки приложения силы давления) h_О = Н/2 ([9], стр.42-43, табл.10)

h_О = Н/2 = 1,2/2 = 0,6 м

Ответ. Сила, действующая на щит, R = 5639,26 Н. Точка приложения силы давления (центр давления) погружена под свободной поверхностью жидкости на глубину h_О = 0,6 м

Вопросы для самоконтроля

3. Как определяется полная результирующая сила давления жидкости на плоскую стенку?

4. Что называется центром тяжести и центром давления, и как определяются их координаты?

5. Что такое гидростатический парадокс?

6. Что такое эпюра гидростатического давления?

7. Какие положения учитываются при построении эпюры гидростатического давления?

8. Как формулируется закон Архимеда?

9. Где на практике применяется закон Архимеда?

10. Назовите гидростатические машины

11. Каково их устройство и принцип действия?

Раздел 3 гидродинамика Тема 3.1 Основы гидродинамики и уравнения движения жидкости Студент должен:

знать:

основные понятия, определения, уравнения гидродинамики; геометрический и энергетический смысл уравнения Бернулли, его практическое применение; принцип действия приборов для измерения скорости и расхода жидкости

уметь:

применять уравнения расхода, неразрывности потока, Бернулли при решении практических задач

Задачи, основные понятия и определения гидродинамики. Гидравлические элементы потока. Расход и средняя скорость потока. Уравнения расхода и неразрывности потока. Уравнение Бернулли для идеальной и реальной жидкости. Энергетический и геометрический смысл уравнения Бернулли. Примеры практического применения уравнений гидродинамики. Измерение скорости и расхода. Мощность потока и мощность насоса. Принцип действия гидравлических машин.

Лабораторная работа 2

Экспериментальная иллюстрация уравнения Бернулли.

Практическое занятие 2

Применение уравнений гидродинамики при решении задач

Литература. [2], стр.55-83; [9], стр.57-99; [11], стр.50-80; [7], стр.25-45