Вопросы для самоконтроля

1. Что называется фильтрацией?

2. Что называется коэффициентом пористости и просветности?

3. Что называется скоростью фильтрации и скоростью движения, и какая из этих скоростей больше?

4. Что называется проницаемости породы, и в каких единицах она измеряется?

5. Что называется приведенным давлением?

6. Что такое закон Дарси, и как определяются границы его применения?

7. Что такое параллельно-прямолинейная фильтрация, и каков для нее вид закона Дарси (жидкость несжимаема)?

8. Что такое плоско-радиальная фильтрация?

9. Напишите формулу Дарси для несжимаемой жидкости.

10. Каков вид записи законов распределения давления для несжимаемой жидкости для параллельно-прямолинейной и плоско-радиальной фильтрации?

11. Чем усложняется вывод формул фильтрации для газа?

12. Что называется функцией Лейбензона и как она определяется?

13. Напишите формулу Дюпюи для газа.

Тема 3.6 Неньютоновские жидкости

Студент должен:

знать:

классификацию и свойства неньютоновских жидкостей; основы гидравлического расчета при движении вязко-пластичных жидкостей

уметь:

определять потери напора (давления), скорость и расход при движении неньютоновских жидкостей

Общие понятия и классификация неньютоновских жидкостей. Вязко-пластичные жидкости и их свойства. Движение вязко-пластичных жидкостей в трубах. Неньютоновские жидкости, применяемые в бурении и эксплуатации скважин. Дисперсные среды.

Литература. [2], стр.196-206; [9], стр.248-254; [11], стр.209-220

Методические указания

Общие понятия и классификация неньютоновских жидкостей

Реологические свойства – это свойства жидкостей, от которых зависит характер их течения.

Ньютоновские жидкости – это такие жидкости, которые подчиняются основному закону внутреннего трения, - закону Ньютона.

τ = μ·(dv/dy) = μ·v,

где τ – касательное напряжение (напряжение сдвига, напряжение трения) – это сила сопротивления (трения), приходящаяся на единицу площади соприкосновения слоев жидкости;

dv/dy = v – градиент скорости (скорость сдвига, скорость скольжения) – это изменение скорости в направлении, нормальном к направлению самой скорости.

Неньютоновские жидкости – это такие жидкости, которые не подчиняются основному закону внутреннего трения, – закону Ньютона.

Основной характеристикой неньютоновской жидкости являются так называемые кривые течения или реологические кривые (реограммы), графически изображающие зависимость между градиентом скорости течения жидкости (скорости сдвига) v и возникающим в жидкости касательным напряжением τ.

Рисунок 2.16 – Реограммы: 1 – дилатантная жидкость; 2 – ньютоновская жидкость; 3 – псевдо-пластичная жидкость; 4 – вязко-пластичная жидкость

Для ньютоновских жидкостей кривые течения носят линейный характер, описываются уравнением τ = μ·v и на графике изображаются прямой линией, проходящей через начало координат (рисунок 2.16, линия 2). Вязкость этих жидкостей определяется углом наклона прямой реограммы к горизонтальной оси μ = ctg α = τ/v. Вязкость является единственной постоянной в ньютоновских жидкостях, полностью определяющей реологические свойства жидкости при данных температуре и давлении независимо от градиента скорости.

Кривые течения неньютоновских жидкостей весьма многообразны и в общем случае не являются линейными. Расположение этих кривых на графике (рисунок 2.16, линии 1; 3; 4) и их форма определяют класс неньютоновских жидкостей и характеризуют особенности их течения. Кривые течения псевдо-пластичных и дилатантных жидкостей хорошо описываются степенной зависимостью вида

τ = k·vⁿ,

где k и n – постоянные для данной жидкости величины.

Величина k представляет собой меру консистенции (густоты) жидкости. Показатель степени n характеризует степень неньютоновского поведения жидкости: чем больше он отличается от 1, тем сильнее проявляются ее неньютоновские свойства. Для псевдо-пластичной жидкости n<1; для дилатантной – n>1.

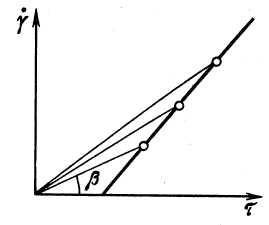
Для характеристики реологических свойств неньютоновских жидкостей часто вводят понятие эффективной кажущейся вязкости μ_э, которая представляет собой некоторую условную характеристику этих жидкостей, используемую при выполнении гидравлических расчетов по обычным формулам гидравлики ньютоновских жидкостей. Эта вязкость даже для определенной жидкости не является постоянной величиной. Ее значение зависит от градиента скорости v и напряжения сдвига τ и определяется на реограмме углами β наклонов прямых, соединяющих начало координат с точками кривой течения (рисунок 2.17).

μ_э = ctg β = τ/v

Рисунок 2.17 – Зависимость градиента скорости от напряжения сдвига

У псевдо-пластичных жидкостей эффективная вязкость μэ с увеличением τ и v уменьшается. Эти жидкости при течении как бы разжижаются. У дилатантных жидкостей, наоборот, при возрастании τ и v эффективная вязкость μэ увеличивается; жидкости при течении как бы загустевают. Наиболее часто в нефтяной промышленности встречаются и применяются неньютоновские вязко-пластичные жидкости.

Свойства вязко-пластичных жидкостей

Вязко-пластичные жидкости совмещают в себе свойства как вязкой жидкости, так и твердого пластичного тела.

Идеальное пластичное тело – это тело, в котором при малых действующих нагрузках, а, следовательно, и малых напряжениях возникают упругие деформации. После снятия нагрузки эти деформации исчезают, и тело восстанавливает свою первоначальную форму.

Когда напряжение достигает некоторого предельного значения τ₀, называемого пределом текучести или начальным напряжением сдвига, пластичное тело начинает течь. В дальнейшем это напряжение сохраняется постоянным при любых значениях относительно скорости сдвига. Течение вязко-пластичной жидкости (как и идеального пластичного тела) начинается при напряжении, равном начальному напряжению сдвига τ₀, и продолжается при напряжениях, изменяющихся по линейному закону, как у обычных ньютоновских жидкостей. Уравнение такой кривой имеет вид

τ = τ₀ + μ·v.

Эту зависимость в 1916 году установил и описал американский ученый Бингам. Поэтому вязко-пластичные жидкости часто называют бингамовскими жидкостями.

Реологические свойства бингамовской жидкости характеризуются двумя основными параметрами:

1. начальным напряжением сдвига τ₀. На реограмме это отрезок оси абсцисс, отсекаемый кривой течения от начала координат.

2. бингамовской или пластичной вязкостью, определяемой по углу α наклона кривой течения к той же оси

μ_пл = ctg α = (τ–τ₀)/v.

При гидравлических расчетах используют также понятие эффективной вязкости, которая в этом случае определяется выражением:

μ_э = ctg β = μ_пл + τ₀/v.

Механизм поведения бингамовских жидкостей можно объяснить образованием в покоящейся жидкости жесткой пространственной решетки (например, у парафинистых нефтей из кристаллов парафина), заполненной жидкой фазой (нефтью). Жесткость решетки такова, что она приводит к полной потере подвижности и достаточна для того, чтобы сопротивляться любому напряжению, не превосходящему по величине τ₀. Если напряжение превышает τ₀, то структура разрушается, и система ведет себя как обычная ньютоновская жидкость при напряжении сдвига τ – τ₀. Когда напряжение становится меньше τ₀, структура снова восстанавливается.

Для многих неньютоновских жидкостей начальное напряжение сдвига в значительной степени зависит от времени нахождения жидкости в покое. Как правило, с течением времени консистенция этих жидкостей изменяется – они как бы застудневают, и их начальное напряжение сдвига увеличивается. Это свойство неньютоновских жидкостей называется тиксотропией, а подобные жидкости – тиксотропными.

В общем случае необходимо различать статическое начальное напряжение сдвига τ_0(ст), характеризующее напряжение в начальный момент движения, когда жидкость выводится из состояния покоя, и динамическое начальное напряжение сдвига τ_0(д), представляющее собой минимальное напряжение, необходимое для движения, если рассматривать жидкость как бингамовскую.

Статическое начальное напряжение сдвига необходимо знать для решения различных задач, в которых рассматриваются начальные (пусковые) стадии движения. Пример подобной задачи – расчет процесса выталкивания насосами застывшей парафинистой нефти из остановленного трубопровода. Во всех остальных случаях при обычных гидравлических расчетах, связанных с движением неньютоновских жидкостей в различных гидравлических системах, используют динамическое напряжение сдвига.

Движение вязко-пластичных жидкостей в трубах

1 2 d р 1 р2 1 L 2 Рисунок 2.18 – Схема трубопровода

Для начала движения неньютоновской жидкости необходимо создать некоторую разность напоров, при которой возникающее в жидкости касательное напряжение τ становится равным ее начальному напряжению сдвига τ0. При этом вся масса жидкости отрывается от стенок трубы и движется первоначально как одно целое (как твердое тело) с одинаковыми для всех частиц скоростями.

Разность давлений Δp₀ на концах трубопровода, необходимая для начала движения, равна

Δp₀ = р₁ – р₂ = 4·τ_о·L/d.

Разность напоров в тех же сечениях

ΔН = Н₁ – Н₂ = 4·τ_о·L/(ρ·g·d).

Если ΔН ≥ 4·τ_о·L/(ρ·g·d), то жидкость в трубопроводе будет двигаться.

В зависимости от приложенной разности напоров возможны два режима движения бингамовской жидкости: структурный и турбулентный.

В начале движения неньютоновской жидкости весь поток жидкости движется целиком как твердое тело с одинаковой скоростью по всему поперечному сечению. По мере увеличения разности давлений или напоров возрастает и скорость движения жидкости, а радиус ее

центральной части (так называемого ядра), где жидкость по-прежнему продолжает двигаться как твердое тело, постепенно уменьшается. Режим движения жидкости, характеризующийся наличием центрального ядра, называют структурным.

Рисунок 2.19 – Кривая скоростей

Радиус центрального ядра r0 равен r0 = 2·τ0·L/Δp = 2·τ0·L/(ρ·g·ΔН) Скорости при структурном режиме распределяются по закону v = [Δp/(4·μпл·L)]·(r2 – y2) – (τ0/μпл)·(r – y). Кривая скоростей, соответствующая этой формуле, представлена на рисунке 2.19. Она состоит из двух параболических ветвей у стенок в зоне так называемого градиентного слоя и прямолинейного участка в ядре.

Для определения скорости движения ядра необходимо принять y = r₀. Тогда

v₀ = [Δp/(4·μ_пл·L)]·(r² – r₀²) – (τ₀/μ_пл)·(r – r₀)

Расход жидкости при структурном режиме равен сумме расходов в ядре и в градиентном слое

Q = [π·r²/(8·μ_пл·L)]·[Δp – ⁴/₃Δp₀ + ¹/₃(Δp₀⁴/Δp³)] – формула Букингама,

где Δp – приложенная разность давлений;

Δp₀ – разность давлений, соответствующая началу движения жидкости.

При технических расчетах последним членом в скобках из-за его малости можно пренебречь.

Потери напора при движении бингамовских жидкостей можно определить по обычной формуле Дарси-Вейсбаха.

При структурном режиме коэффициент гидравлического сопротивления

λ = 64/Re*,

где Re* – обобщенное число Рейнольдса, учитывающее одновременно как вязкие, так и пластические свойства жидкости

Re* = Re/(1 + А·Sen),

где Re – обычное число Рейнольдса;

А – коэффициент, зависящий от структуры потока, которая определяется радиусом его центрального ядра. В расчетах принимается А = ¹/₆;

Sen – число Сен-Венана (характеристика пластических свойств жидкости)

Sen = τ₀·d/(v·μ_пл) = τ₀·d³·π/(4·Q·μ_пл)

Таким образом, обобщенное число Рейнольдса равно

Re* = Re/[1 + ¹/₆ Sen] = 1/[(μ_пл/(ρ·v·d) + τ₀/(6·ρ·v²)]

Переход структурного режима в турбулентный осуществляется при Re*_кр > 2000 ÷ 3000.

При турбулентном режиме для определения коэффициента гидравлического сопротивления λ применяют формулы типа

λ = В/ Re*ⁿ,

где В – коэффициент и n – показатель степени, которые наиболее достоверно устанавливаются по результатам обработки опытных данных ([2], стр.204; [11], стр.218).