Пример решения задачи по теме 3.3 Движение жидкости в трубопроводах

Построить характеристику трубопровода с наружным диаметром 159 мм, толщиной стенки 5 мм, пропускная способность которого 100 м³/ч воды. Трубы старые стальные.

Дано	СИ
D = 159 мм	D = 0,159 м
δ = 5 мм	δ = 0,005 м
Q = 100 м3/ч	Q= 100/3600 = 1/36 = 0,028 м3/с
Построить характеристику трубопровода

Решение

Гидравлической характеристикой трубопровода называется аналитическая или графическая зависимость потери напора в трубопроводе от расхода (пропускной способности – это количество жидкости, протекающее через поперечное сечение трубопровода в единицу времени). Чтобы выбрать уравнение для построения характеристики трубопровода, определяют режим движения воды и зону трения.

Определяется внутренний диаметр трубопровода

d = D-2·δ, м,

где D - наружный диаметр трубопровода, м; D = 0,159 м;

δ - толщина стенки трубопровода, м; δ = 0,005 м

d = 0,159-2·0,005 = 0,149 м

Определяется скорость движения воды

v = 4·Q/(π·d²) = 4·1/(36·3,14·0,149²) = 1,59 м/с

Определяется режим движения воды, который характеризуется величиной числа Рейнольдса

Re = v·d/ν,

где ν – кинематическая вязкость воды, м²/с. При температуре 20°С кинематическая вязкость воды ν = 1 сСт = 1·10^-6 м²/с ([2], стр. 14).

Re = 1,59·0,149/1·10^-6 = 237488

Так как Re > 2300 (237488 > 2300), то режим движения турбулентный. Турбулентное движение – это движение жидкости при больших скоростях, когда в движении нет видимой закономерности, и отдельные частицы, перемешиваясь между собой, движутся хаотично.

Для определения зоны трения находится первое переходное число Рейнольдса

Re_1пер = 40·d/k,

где d – внутренний диаметр трубопровода;

k – абсолютная шероховатость стенок труб. Абсолютная шероховатость k – это величина выступов и неровностей внутренней поверхности труб, измеренная в линейных единицах (в мм или в м). Для старых стальных труб рекомендуется k = 0,5÷2,0 мм ([9], стр.135, табл.16). Выбирается k = 1,0 мм = 1,0·10^-3 м

Re_1пер = 40·0,149/1,0·10^-3 = 5960

Так как Re > Re_1пер (237488 > 5960), то находится второе переходное число Рейнольдса

Re_2пер = 500·d/k = 500·0,149/1,0·10^-3 = 74500

Так как Re > Re_2пер (Re > 500000), то зона вполне шероховатых труб (квадратичная зона). В этой зоне характеристический коэффициент трубопровода

B = (π/4)·√2·g/λ ([9], стр.218, табл.44)

где λ – коэффициент гидравлического сопротивления. В зоне вполне шероховатых труб λ определяется по формуле Никурадзе

λ = 1/[(1,74 - 2·lg ε)²]

где ε – относительная шероховатость стенок труб, м. Относительная шероховатость ε – это отношение абсолютной шероховатости к радиусу трубы

ε = k/r = 2·k/d) = 2·1,0·10^-3 /0,149 = 0,0134

λ = 1/[(1,74 - 2·lg 0,0134)²] = 0,033

B = (3,14/4)·√2·9,81/0,033 = 19,07 ≈ 19

При турбулентном режиме для построения характеристики трубопровода применяется уравнение

ΔH = B·Q²,

где ΔH – потеря напора в трубопроводе;

В – характеристический коэффициент трубопровода;

Q – пропускная способность трубопровода

ΔH = 19·Q²

Таблица 2.2 – Расчетные данные для построения характеристики трубопровода

Пропускная способность трубопровода Q,м3/с	0	0,01	0,02	0,03
Потери напора в трубопроводе ΔH·103, м	0	1,9	7,6	17,1

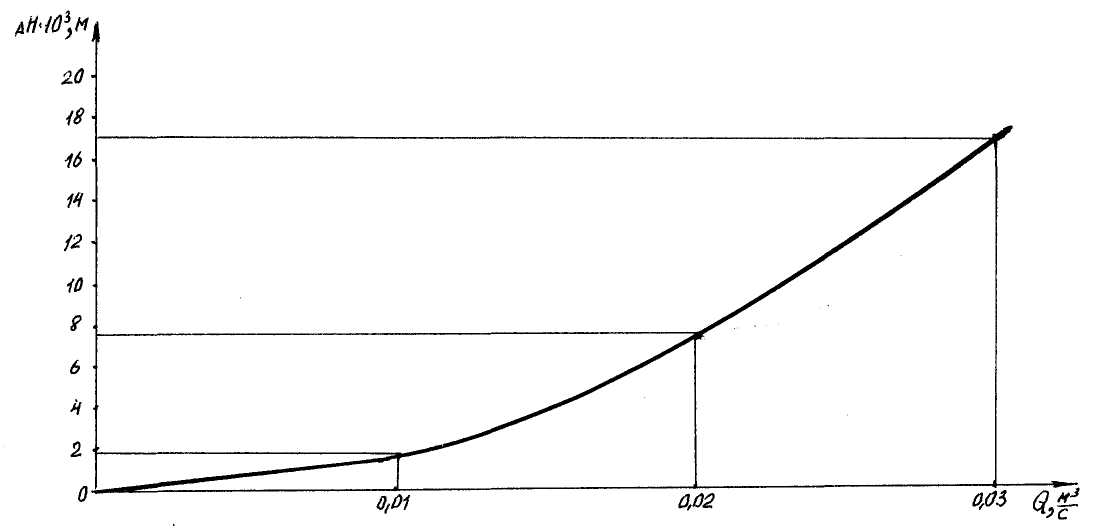
Рисунок 2.6 – Гидравлическая характеристика трубопровода