
- •Глава 2 Базовые понятия реляционной модели данных 21
- •Глава 3. Целостность реляционных данных 28
- •Глава 4. Реляционная алгебра 39
- •Глава 6. Нормальные формы отношений 57
- •Глава 7 Нормальные формы более высоких порядков 74
- •Глава 8. Элементы модели «сущность-связь» 83
- •Глава 5. Элементы языка sql 110
- •Ранние подходы к организации бд. Системы, основанные на инвертированных списках, иерархические и сетевые субд. Примеры. Сильные места и недостатки ранних систем
- •Основные особенности систем, основанных на инвертированных списках
- •Структуры данных
- •Манипулирование данными
- •Ограничения целостности
- •Иерархические системы
- •Иерархические структуры данных
- •Манипулирование данными
- •Ограничения целостности
- •Сетевые системы
- •Сетевые структуры данных
- •Манипулирование данными
- •Ограничения целостности
- •Достоинства и недостатки
- •Элементы теории множеств Множества
- •Операции над множествами
- •Декартово произведение множеств
- •Отношение
- •Примеры отношений Бинарные отношения (отношения степени 2)
- •Отношение эквивалентности
- •Отношения порядка
- •Функциональное отношение
- •Еще пример бинарного отношения
- •Транзитивное замыкание отношений
- •Глава 2 Базовые понятия реляционной модели данных Общая характеристика реляционной модели данных
- •Типы данных
- •Простые типы данных
- •Структурированные типы данных
- •Ссылочные типы данных
- •Типы данных, используемые в реляционной модели
- •Отношения, атрибуты, кортежи отношения Определения и примеры
- •Свойства отношений
- •Первая нормальная форма
- •Глава 3. Целостность реляционных данных
- •Null-значения
- •Трехзначная логика (3vl)
- •Потенциальные ключи
- •Целостность сущностей
- •Внешние ключи
- •Целостность внешних ключей
- •Замечания к правилам целостности сущностей и внешних ключей
- •Операции, могущие нарушить ссылочную целостность
- •Для родительского отношения
- •Для дочернего отношения
- •Стратегии поддержания ссылочной целостности
- •Применение стратегий поддержания ссылочной целостности
- •При обновлении кортежа в родительском отношении
- •При удалении кортежа в родительском отношении
- •При вставке кортежа в дочернее отношение
- •При обновлении кортежа в дочернем отношении
- •Глава 4. Реляционная алгебра Обзор реляционной алгебры
- •Замкнутость реляционной алгебры
- •Отношения, совместимые по типу
- •Оператор переименования атрибутов
- •Теоретико-множественные операторы Объединение
- •Пересечение
- •Вычитание
- •Декартово произведение
- •Специальные реляционные операторы Выборка (ограничение, селекция)
- •Проекция
- •Соединение
- •Общая операция соединения
- •Тэта-соединение
- •Экви-соединение
- •Естественное соединение
- •Деление
- •Примеры использования реляционных операторов
- •Невыразимость транзитивного замыкания реляционными операторами
- •Кросс-таблицы
- •Реляционное исчисление
- •Кортежные переменные и правильно построенные формулы
- •Целевые списки и выражения реляционного исчисления
- •Реляционное исчисление доменов
- •Глава 6. Нормальные формы отношений Этапы разработки базы данных
- •Критерии оценки качества логической модели данных
- •Адекватность базы данных предметной области
- •Легкость разработки и сопровождения базы данных
- •Скорость операций обновления данных (вставка, обновление, удаление)
- •Скорость операций выборки данных
- •Основной пример
- •1Нф (Первая Нормальная Форма)
- •Аномалии обновления
- •Аномалии вставки (insert)
- •Аномалии обновления (update)
- •Аномалии удаления (delete)
- •Функциональные зависимости
- •Определение функциональной зависимости
- •Функциональные зависимости отношений и математическое понятие функциональной зависимости
- •2Нф (Вторая Нормальная Форма)
- •Анализ декомпозированных отношений
- •Оставшиеся аномалии вставки (insert)
- •Оставшиеся аномалии обновления (update)
- •Оставшиеся аномалии удаления (delete)
- •3Нф (Третья Нормальная Форма)
- •Алгоритм нормализации (приведение к 3нф)
- •Анализ критериев для нормализованных и ненормализованных моделей данных Сравнение нормализованных и ненормализованных моделей
- •Oltp и olap-системы
- •Корректность процедуры нормализации – декомпозиция без потерь. Теорема Хеза
- •Глава 7 Нормальные формы более высоких порядков
- •Нфбк (Нормальная Форма Бойса-Кодда)
- •4Нф (Четвертая Нормальная Форма)
- •5Нф (Пятая Нормальная Форма)
- •Продолжение алгоритма нормализации (приведение к 5нф)
- •Глава 8. Элементы модели «сущность-связь»
- •Основные понятия er-диаграмм
- •Нормальные формы er-схем
- •Более сложные элементы er-модели
- •Получение реляционной схемы из er-схемы
- •Пример разработки простой er-модели
- •Концептуальные и физические er-модели
- •Внутренняя организация реляционных субд Cтруктуры внешней памяти, методы организации индексов
- •Хранение отношений
- •Индексы
- •Хэширование
- •Журнальная информация
- •Служебная информация
- •Управление транзакциями, сериализация транзакций
- •Транзакции и целостность баз данных
- •Изолированность пользователей
- •Сериализация транзакций
- •Методы сериализации транзакций
- •Синхронизационные захваты
- •Гранулированные синхронизационные захваты
- •Предикатные синхронизационные захваты
- •Тупики, распознавание и разрушение
- •Метод временных меток
- •Журнализация изменений бд
- •Журнализация и буферизация
- •Индивидуальный откат транзакции
- •Восстановление после мягкого сбоя
- •Физическая согласованность базы данных
- •Восстановление после жесткого сбоя
- •Глава 5. Элементы языка sql
- •Предварительные сведения о работе с sql сервером.
- •InterBase сервер
- •Выполнение в ibConsole
- •Р егистрация псевдонима (алиаса).
- •Пользователи.
- •С оздание модельных бд.
- •Сеанс sql
- •Структура учебных баз данных
- •Операторы sql
- •Операторы ddl (Data Definition Language) - операторы определения объектов базы данных
- •Операторы dml (Data Manipulation Language) - операторы манипулирования данными
- •Операторы dql (Data Query Language) – операторы запросов к данным
- •Операторы dcl (Data Control Language) - защиты и управления данными
- •Основные типы данных
- •Строки фиксированной длины
- •Строки переменной длины
- •Числовые значения
- •Десятичные значения
- •Десятичные значения с плавающей точкой
- •Значения даты и времени
- •Буквальные значения
- •Значения null
- •Значения типа boolean
- •Пользовательские типы данных
- •Типы данных InterBase
- •Управление объектами базы данных
- •Что такое объекты базы данных?
- •Что такое схема?
- •Поля и столбцы
- •Оператор create database
- •Синтаксис
- •Примеры
- •Оператор create table
- •Синтаксис
- •Примеры
- •Ключевое слово storage (в InterBase не действует!)
- •Соглашения о присвоении имен
- •Команда alter table
- •Синтаксис
- •Примеры
- •Модификация элементов таблицы
- •Добавление столбцов, требующих обязательного ввода данных
- •Пример:
- •Изменение столбцов
- •Создание таблицы на основе уже существующей
- •Удаление таблиц
- •Условия целостности
- •Ключевые поля
- •Требования уникальности
- •Внешние ключи
- •Атрибут not null
- •Использование условий проверки
- •Удаление условий
- •Определение представлений
- •Оператор create view (InterBase) Описание
- •Синтаксис
- •Примеры
- •Определение привилегий
- •Оператор grant (InterBase) Описание
- •Синтаксис
- •Примеры
- •Вопросы и ответы
- •Практикум
- •Примеры
- •Манипуляция данными
- •Обзор возможностей манипуляции данными
- •Заполнение таблиц новыми данными
- •Ввод данных в таблицу
- •Ввод данных в определенные столбцы таблицы
- •Ввод данных из другой таблицы
- •Ввод значений null
- •Обновление уже имеющихся данных
- •Обновление значений одного столбца
- •Обновление нескольких столбцов в одной или нескольких записях
- •Удаление данных из таблиц
- •Примеры использования операторов манипулирования данными
- •Знакомство с запросами
- •Что такое запрос?
- •Оператор select
- •Синтаксис оператора выборки данных (select)
- •Синтаксис оператора выборки
- •Синтаксис
- •Примеры
- •Ключевое слово select
- •Ключевое слово from
- •Использование условий для отбора данных
- •Сортировка вывода
- •Учет регистра символов
- •Примеры простых запросов
- •Подсчет записей в таблице
- •Получение данных из таблиц других пользователей
- •Псевдонимы столбцов
- •Упражнения
- •Операции в условиях для отбора данных
- •Что такое операции в sql?
- •Операции сравнения
- •Равенство
- •Неравенство
- •«Меньше» и «больше»
- •Примеры комбинирования операций сравнения
- •Логические операции
- •Использование операторов exists, any, all, и some Описание учебной базы данных
- •Операции конъюнкции и дизъюнкции
- •Отрицание условий с помощью операции отрицания
- •Неравенство
- •Деление
- •Комбинирование арифметических операций
- •Вопросы и ответы
- •Подведение итогов по данным запроса
- •Что такое итоговые функции?
- •Функция count
- •Функция sum
- •Функция avg
- •Функция max
- •Функция min
- •Описание
- •Синтаксис
- •Примеры
- •Описание
- •Примеры
- •Описание
- •Синтаксис
- •Примеры
- •Описание
- •Синтаксис
- •Примеры
- •Описание
- •Синтаксис
- •Примеры
- •Сортировка и группирование данных
- •Зачем группировать данные?
- •Ключевое слово group by
- •Группирование выбранных данных
- •Создание групп и использование итоговых функций
- •Представление имен столбцов числами
- •Ключевое слово having
- •Объединение таблиц в запросах
- •Отбор данных из нескольких таблиц
- •Типы связывания
- •Компоненты условия связывания
- •Связывание по равенству
- •Естественное связывание
- •Использование псевдонимов для имен таблиц
- •Связывание по неравенству
- •Внешнее связывание
- •Рекурсивное связывание
- •Связывание по нескольким ключам
- •Вопросы связывания
- •Использование связующей таблицы
- •Декартово произведение
- •Вопросы и ответы
- •Практикум
- •Упражнения
- •Использование подзапросов
- •Что такое подзапрос?
- •Подзапросы в операторе select
- •Подзапросы в операторе insert
- •Подзапросы в операторе update
- •Подзапросы в операторе delete
- •Подзапросы внутри подзапросов
- •Связанные подзапросы
- •Объединение запросов
- •Обычные и составные запросы
- •Зачем использовать составные запросы?
- •Команды построения сложных запросов
- •Команда union
- •Команда union all
- •Команда intersect
- •Команда except
- •Использование order by в составных запросах
- •Использование group by в составных запросах
- •Обеспечение правильности результатов
- •Примеры использования оператора select
- •Отбор данных из одной таблицы
- •Отбор данных из нескольких таблиц
- •Использование имен корреляции (алиасов, псевдонимов)
- •Использование агрегатных функций в запросах
- •Использование агрегатных функций с группировками
- •Использование подзапросов
- •Использование объединения, пересечения и разности
- •Синтаксис соединенных таблиц
- •Синтаксис условных выражений раздела where
- •Порядок выполнения оператора select
- •Стадия 1. Выполнение одиночного оператора select
- •Стадия 2. Выполнение операций union, except, intersect
- •Стадия 3. Упорядочение результата
- •Как на самом деле выполняется оператор select
- •Оператор соединения
- •Оператор пересечения
- •Оператор деления
- •Использование индексов для ускорения поиска данных
- •Что такое индекс?
- •Принцип работы индексов
- •Команда create index
- •Типы индексов
- •Простые индексы
- •Уникальные индексы
- •Составные индексы
- •Простые и составные индексы
- •Неявные индексы
- •Когда следует создавать индекс?
- •Когда не следует создавать индекс?
- •Удаление индексов
- •Повышение эффективности работы с базой данных
- •Что означает оптимизация операторов sql?
- •Оптимизация базы данных и оптимизация операторов sql
- •Форматирование операторов sql
- •Форматирование операторов для лучшего восприятия
- •Правильный порядок таблиц в выражении from
- •Правильный порядок условий связывания
- •Наиболее ограничительное условие
- •Полное сканирование таблиц
- •Когда и как избегать полного сканирования таблиц
- •Другие аспекты оптимизации
- •Использование like и знаков подстановки
- •Замена операций or выражением с ключевым словом in
- •Недостатки использования выражения с ключевым словом having
- •Долгие операции сортировки
- •Использование готовых процедур
- •Отмена использования индексов в больших пакетных операциях
- •Средства для анализа производительности
- •Создание и использование представлений и синонимов
- •Что такое представление?
- •Использование представлений для защиты данных
- •Использование представлений для управления выводом данных
- •Хранение представлений
- •Создание представлений
- •Создание представления для данных одной таблицы
- •Создание представления для данных нескольких таблиц
- •Создание представления на основе другого представления
- •Уровни зависимости представлений
- •Опция with check option
- •Опции cascaded и local
- •Синтаксис
- •Примеры
- •Обновление данных представления
- •Представления и выражение order by
- •Удаление представлений
- •Что такое синонимы? (InterBase не поддержвается)
- •Управление синонимами
- •Создание синонимов
- •Удаление синонимов
- •Триггеры и хранимые процедуры (InterBase) sql для триггеров и хранимых процедур в InterBase
- •Обработка исключений
- •Обработка ошибок sql
- •Обработка ошибок InterBase
- •Комментарий
- •Триггеры и их назначение
- •Синтаксис create trigger
- •Примеры
- •Дополнительные сведения по работе с генераторами
- •Хранимые процедуры и их назначение
- •Процедуры для работы с датой и временем
Примеры отношений Бинарные отношения (отношения степени 2)
В математике
большую роль играют бинарные отношения,
т. е. отношения, заданные на декартовом
произведении двух множеств
![]() .
.
Отношение эквивалентности
Определение 8. Отношение R на множестве A2 называется отношением эквивалентности, если оно обладает следующими свойствами:
 для всех
(рефлексивность);
для всех
(рефлексивность);
Если
 ,
то
,
то
 (симметричность);
(симметричность);
Если и
 ,
то
,
то
 (транзитивность).
(транзитивность).
Обычно отношение эквивалентности обозначают знаком « = » или « ≈ » и говорят, что оно (отношение) задано на множестве A (а не на A2). Условия 1 ÷ 3 в таких обозначениях выглядят более естественно:
 для всех
(рефлексивность);
для всех
(рефлексивность);
Если
 ,
то
,
то
 (симметричность);
(симметричность);
Если и
 ,
то
,
то
 (транзитивность).
(транзитивность).
Легко доказывается, что если на множестве A задано отношение эквивалентности, то множество A разбивается на взаимно непересекающиеся подмножества, состоящие из эквивалентных друг другу элементов (классы эквивалентности).
Пример 1.
Рассмотрим на множестве вещественных
чисел
![]() отношение, заданное просто равенством
чисел. Предикат такого отношения:
отношение, заданное просто равенством
чисел. Предикат такого отношения:
|
Условия 1 ÷ 3, очевидно, выполняются, поэтому данное отношение является отношением эквивалентности. Каждый класс эквивалентности этого отношения состоит из одного числа.
Пример 2. Рассмотрим более сложное отношение эквивалентности. На множестве целых чисел Z зададим отношение «равенство по модулю n» следующим образом: два числа a и b равны по модулю n, если их остатки при делении на n равны. Например, по модулю 5 равны числа 2, 7, 12 и т. д.
Условия 1 ÷ 3 легко проверяются, поэтому равенство по модулю является отношением эквивалентности. Предикат этого отношения имеет вид:
|
Классы эквивалентности этого отношения состоят из чисел, дающих при делении на n одинаковые остатки. Таких классов ровно n:
[0] = {0, n, 2n, …} |
[1] = {1, n + 1, 2n + 1, …} |
… |
[n - 1] = {n - 1, n + n - 1, 2n + n - 1, …} |
Отношения порядка
Определение 9.
Отношение
![]() на
множестве
на
множестве
![]() называется
отношением
порядка,
если оно обладает следующими свойствами:
называется
отношением
порядка,
если оно обладает следующими свойствами:
 для
всех
для
всех
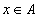 (рефлексивность)
(рефлексивность)
Если
 и
и
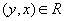 ,
то
,
то
 (антисимметричность)
(антисимметричность)
Если и
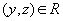 ,
то
,
то
 (транзитивность)
(транзитивность)
Обычно отношение
порядка обозначают знаком
![]() .
Если для двух элементов
.
Если для двух элементов
![]() и
и
![]() выполняется
выполняется
![]() ,
то говорят, что
"предшествует"
.
Как и для отношения эквивалентности,
условия 1-3 в таких обозначениях выглядят
более естественно:
,
то говорят, что
"предшествует"
.
Как и для отношения эквивалентности,
условия 1-3 в таких обозначениях выглядят
более естественно:
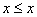 для
всех
(рефлексивность)
для
всех
(рефлексивность)
Если и
 ,
то
(антисимметричность)
,
то
(антисимметричность)
Если и
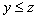 ,
то
,
то
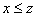 (транзитивность)
(транзитивность)
Пример 3.
Простым примером отношения порядка
является отношение, задаваемое обычным
неравенством
на
множестве вещественных чисел
![]() .
Заметим, что для
любых чисел
и
выполняется
либо
,
либо
,
т.е. любые
два числа
сравнимы между собой. Такие отношения
называются отношениями
полного порядка.
.
Заметим, что для
любых чисел
и
выполняется
либо
,
либо
,
т.е. любые
два числа
сравнимы между собой. Такие отношения
называются отношениями
полного порядка.
Предикат данного отношения есть просто утверждение .
Пример 4.
Рассмотрим на множестве
![]() всех
сотрудников некоторого предприятия
отношение, задаваемое следующим образом:
сотрудник
предшествует
сотруднику
тогда
и только тогда, когда выполняется одно
из условий:
всех
сотрудников некоторого предприятия
отношение, задаваемое следующим образом:
сотрудник
предшествует
сотруднику
тогда
и только тогда, когда выполняется одно
из условий:
является начальником (не обязательно непосредственным)
Назовем такое отношение "быть начальником". Легко проверить, что отношение "быть начальником" является отношением порядка. Заметим, что в отличие от предыдущего примера, существуют такие пары сотрудников и , для которых не выполняется ни , ни (например, если и являются сослуживцами). Такие отношения, в которых есть несравнимые между собой элементы, называют отношениями частичного порядка.
