Кінематичне дослідження важільних механізмів

Лабораторна робота №2

Кінематичне дослідження важільних механізмів

Мета роботи: ознайомитися з практичними способами кінематичного дослідження важільних механізмів аналітичним методом за допомогою ЕОМ, методом кінематичних діаграм та методом планів швидкостей та прискорень.

Теоретичні відомості

При конструюванні нових або дослідженні діючих механізмів необхідно знайти траєкторії, швидкості і прискорення точок, а також положення, кутові швидкості і прискорення ланок механізму. Визначення вказаних параметрів називається кінематичним дослідженням механізму. Ці параметри визначають аналітичним, графічним, графоаналітичним або експериментальним методами.

А Аналітичний метод

При кінематичному дослідженні аналітичним методом необхідно визначити залежність координат вихідної ланки через координати ведучої ланки, закон руху якої заданий.

Як правило, для більшості механізмів число незалежних параметрів, якими можна задаватися довільно, відповідає числу ступенів рухомості. Для плоских механізмів ступінь рухомості визначається за формулою П.Л.Чебишева:

W = 3n - 2p5 - p4,

де n – число рухомих ланок механізму;

р_і – число кінематичних пар і-го класу (і=1, 2, 3...5).

Наприклад, для кривошипно-повзункового механізму, кінематична схема якого зображена на рис. 4.1а, ступінь рухомості дорівнює:

W = 3n - 2p5 - p4 = 33-24-0=1.

Це означає, що при W=1 механізм має один незалежний параметр, або одну узагальнену координату, яка визнає положення будь-якої ланки механізму. На практиці зручніше за узагальнену координату приймати кут φ₁, що визначає положення ведучої ланки кривошипа (рис. 2.1а.).

В основу аналітичної кінематики механізмів покладено метод Зінов’єва, згідно з яким будь-який механізм, що складається із замкненого кінематичного ланцюга з нижчими парами, можна зобразити у вигляді замкненого векторного контуру або системи замкнутих векторних контурів, замінивши умовно ланки механізму векторами. За початок векторного контуру зручно приймати нерухому точку (стояк). Кожен вектор має початком та кінцем кінематичні пари, в які входять ланки. Модуль вектора може бути як постійним, так і змінним. Напрямок кожного вектора визначається кутом, що відраховується проти годинникової стрілки від лінії, яка паралельна осі х обраної системи координат і проведена через початок відповідного вектора. Знак вектора береться плюс, якщо напрям вектора збігається з напрямом обходу контуру за годинниковою стрілкою.

1 Аналітика кривошипно-повзункового механізму

Зображаємо кривошипно-повзунковий механізм у вигляді векторного многокутника (рис. 2.1а.). нанесемо певним чином на ланки групи вектори, які утворюють замкнений контур. Запишемо умову замкненості контуру у вигляді векторного рівняння:

.

(2.1)

Приймаємо точку О – центр обертання кривошипа – за початок системи координат OXY. Враховуючи умову замкненості, запишемо рівняння проекцій векторів на осі х і у:

,	(2.2)
.	(2.3)

Використовуючи рівняння (2.2) і (2.3), отримуємо функції положення ланок і точок механізму:

,	(2.4)
,	(2.5)

де .

Рівнянням (2.4) визначається лінійне переміщення повзуна, а рівнянням (2.5) – кутове переміщення повзуна.

При диференціюванні рівнянь (2.4) і (2.5) за незалежний параметр механізму можна прийняти час t або кут φ₁ повороту кривошипа. У першому випадку отримаємо залежності для визначення швидкості і прискорення, а у другому – аналоги швидкості і прискорення ланок механізму і точок, що їм належать.

Диференціюємо рівняння (2.5.) за часом t. Тоді кутова швидкість шатуна:

.

(2.6)

Диференціюючи рівняння (2.5) за узагальненою координатою φ₁, отримаємо залежність аналога кутової швидкості шатуна:

(2.7)

Аналог кутової швидкості шатуна і₂₁ є безрозмірною величиною і являє собою передаточну функцію, або передаточне відношення між ланками, у даному випадку між шатуном 2 і кривошипом 1.

Зв’язок між кутовою швидкістю ₂ і її аналогом і₂₁:

.

(2.8)

Для визначення кутового прискорення ε₂ шатуна диференціюємо за часом t рівняння (2.6):

(2.9)

Аналог кутового прискорення шатуна визначається диференціюванням рівняння (2.7)

(2.10)

Зв’язок між кутовим прискоренням ₂ шатуна і його аналогом

.

(2.11)

Для визначення лінійних швидкостей і прискорень повзунка використаємо рівняння (2.4), двічі його диференціюючи

;	(2.12)
	(2.13)

Аналоги швидкостей і прискорень повзунка виражаються такими залежностями:

,	(2.14)
	(2.15)

Зв’язок між швидкостями, прискореннями і їх аналогами можна подати таким чином:

,	(2.16)
.	(2.17)
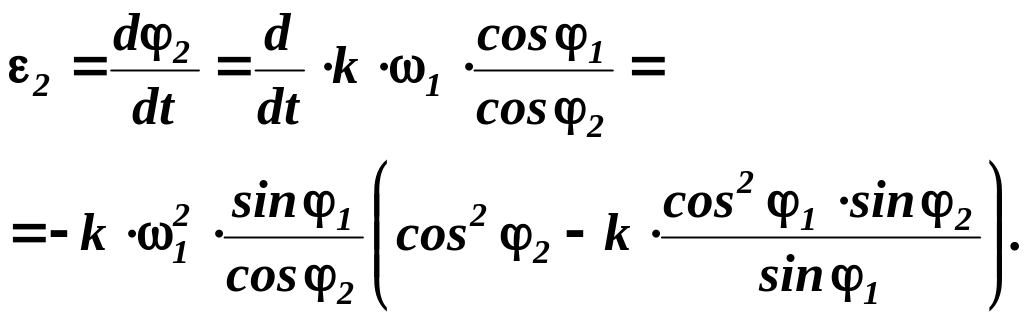
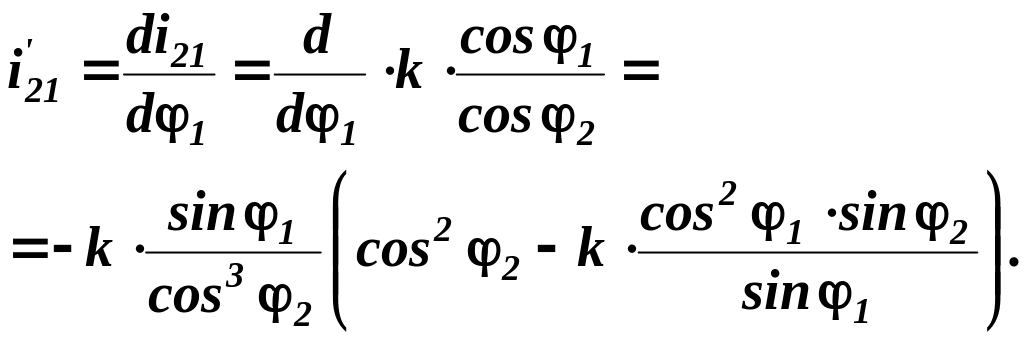
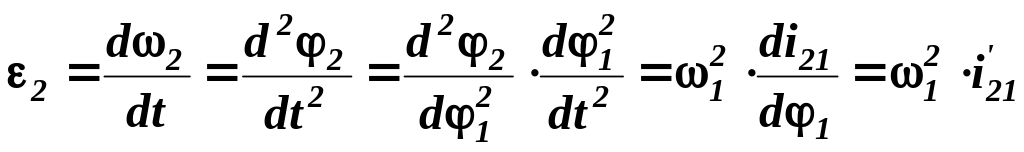