{Ниже - нормировка распределений g и h}

for i:=1 to 11 do begin L1[i]:=L1[i]/n; L2[i]:=L2[i]/n end; s1:=s1/n; s2:=s2/n; Dg:=0; Dh:=0;

{Ниже - расчет средних и дисперсий g и h}

for i:=1 to n do begin Dg:=Dg+sqr(g[i]-s1); Dh:=Dh+sqr(h[i]-s2) end; Dg:=Dg/n; Dh:=Dh/n; for i:=1 to 11 do memo1.Lines.Add(floattostr(L1[i])); for i:=1 to 11 do memo2.Lines.Add(floattostr(L2[i])); memo1.Lines.Add('СРЕДНЕЕ G='+floattostr(s1)); memo2.Lines.Add('СРЕДНЕЕ H='+floattostr(s2)); memo1.Lines.Add('СР-КВАДР. G='+floattostr(Dg)); memo2.Lines.Add('СР-КВАДР. H='+floattostr(Dh)); end; procedure TForm1.Button2Click(Sender: TObject); begin memo1.Clear; memo2.Clear; button1.Click end; procedure TForm1.Button3Click(Sender: TObject); begin close end; procedure TForm1.Button4Click(Sender: TObject); begin form2.Show end; end.

Графики распределений:

unit Unit2; interface uses Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms, Dialogs, StdCtrls; type TForm2 = class(TForm) procedure Form2Paint(Sender: TObject); private { Private declarations } public { Public declarations } end; var Form2: TForm2; implementation uses Unit1; {$R *.dfm} procedure TForm2.Form2Paint(Sender: TObject); var w,h,s,i1,i2:integer; begin with form2.Canvas do begin w:=width; h:=height; s:=w div 2; textout(20,50,'p'); textout(s+12,h-80,'p'); textout(200,50,'w1'); textout(s+200,h-80,'w2'); moveto(10,h-100);lineto(s,h-100); moveto(10,h-100);lineto(10,50); max:=L1[1]; for i1:=2 to 11 do if L1[i1]>max then max:=L1[i1]; for i1:=2 to 11 do v[i1]:=L1[i1]/max; for i1:=2 to 11 do begin i2:=round((h-110)*(1-v[i1]))+10; brush.Color:=rgb(random(105)+150,random(105)+150,random(105)+150); rectangle(50*i1-90,i2,50*i1-40,h-100) end; moveto(s+10,h-100);lineto(w-20,h-100);moveto(s+10,h-100);lineto(s+10,50); max:=L2[1]; for i1:=2 to 11 do if L2[i1]>max then max:=L2[i1]; for i1:=2 to 11 do v[i1]:=L2[i1]/max; for i1:=2 to 11 do begin i2:=round((h-110)*(1-v[i1]))+10; brush.Color:= rgb(random(105)+150,random(105)+150,random(105)+150); rectangle(s-90+50*i1,i2,s-40+50*i1,h-100) end; end; end; end.

Результаты работы программы представлены на рисунках 19-20:

Рисунок 19. Результат работы Unit1

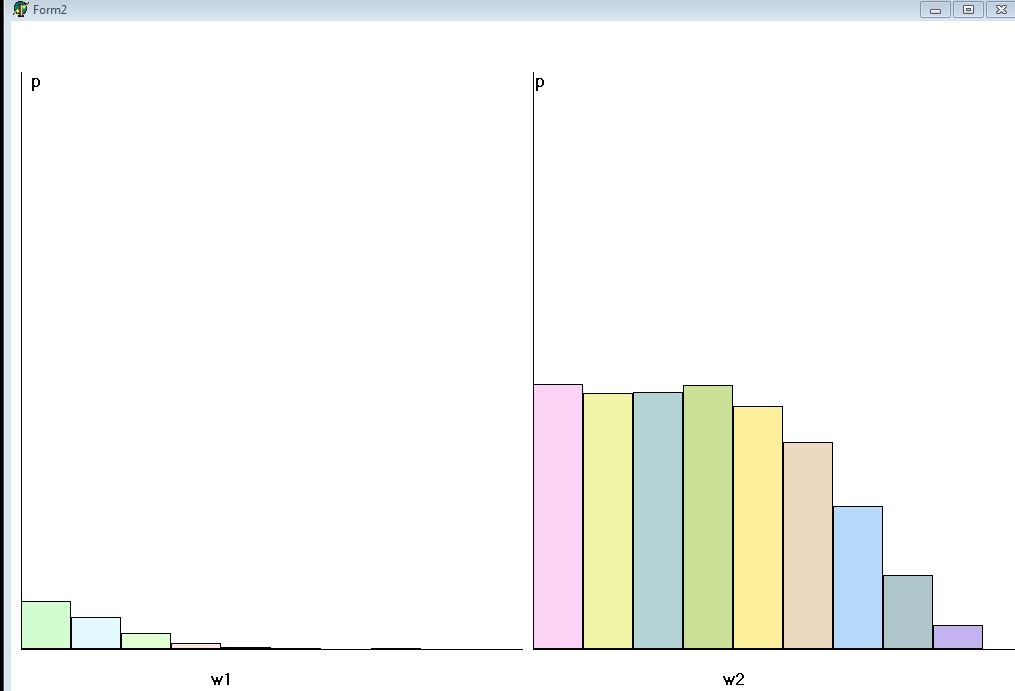
Рисунок 20. График распределения величин g и h при w1=10 и w2=4.

Оценим адекватность полученной модели. Для оценки адекватности выполняются следующие действия:

1. Задаемся доверительной вероятностью β. Рекомендуемое значение β=0,95. По статистическим таблицам находим t, которое для рекомендуемого значения β=0,95 равно 1,96.

2. Задаемся количеством проводимых экспериментов N.

3. Вычисляем половину ширины доверительного интервала: 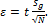В качестве S_g берется среднее квадратическое отклонение, вычисленное при аналитическом моделировании.

4. Подсчитываем количество попаданий оценок математических ожиданий в доверительный интервал по выполнению условия: M_g-ε≤M_g≤M_g+ε. В качестве M_g берется математическое ожидание, вычисленное при аналитическом моделировании.

Если количество попаданий оценок математических ожиданий в доверительный интервал не меньше β*N, то имитационную модель считаем пригодной по тесту адекватности.

Если N большое, то количество попаданий оценок математических ожиданий в доверительный интервал сравнивается с количеством серий испытаний.

В таблице 2 приведены результаты расчета средних значений величин g, h и соответствующих средних квадратических отклонений S_g, S_h, полученные при одинаковых значениях всех параметров в пяти разных сериях испытаний по 10000 событий в серии. w₁=10, w₂=4.

Испытание
1	0,400	0,969	2,996	7,149
2	0,414	0,997	3,015	7,340
3	0,391	0,976	3,026	7,280
4	0,413	0,960	2,974	7,199
5	0,399	0,878	3,000	7,314

Таблица 2

Оценим доверительный интервал математических ожиданий величин g и h достоверности 0. По первой выборке получаем:

0,400–0,019<M_g<0,400+0,019 ⇒ 0,381<M_g<0,419 2,996–0,140<M_h<2,996+0,140 ⇒ 2,856<M_h<3,136

Таким образом, различия в выборочных средних вполне укладываются в указанные доверительные интервалы.

В рассмотренной задаче может возникнуть критическая ситуация, когда очередь неограниченно растет со временем. В самом деле, если люди заходят в магазин очень часто (или продавец работает слишком медленно), очередь начинает нарастать, и в любой системе с конечным временем обслуживания наступит кризис. Приведем для иллюстрации динамики этого процесса распределения величин – времени ожидания покупателем в очереди и – времени простоя продавца в ожидании покупателя, при трех наборах параметров где – максимальный интервал времени между приходами покупателей, – максимальная длительность обслуживания покупателя (рис. 21-22):

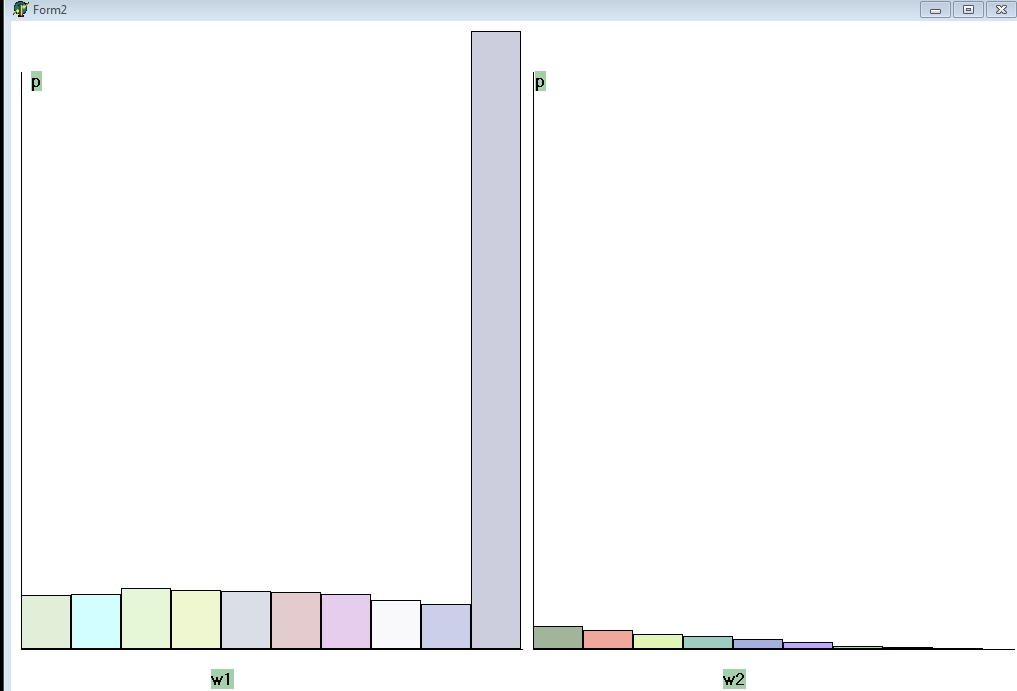
Рисунок 21. Кризис наступает, w₁=10; w₂=9

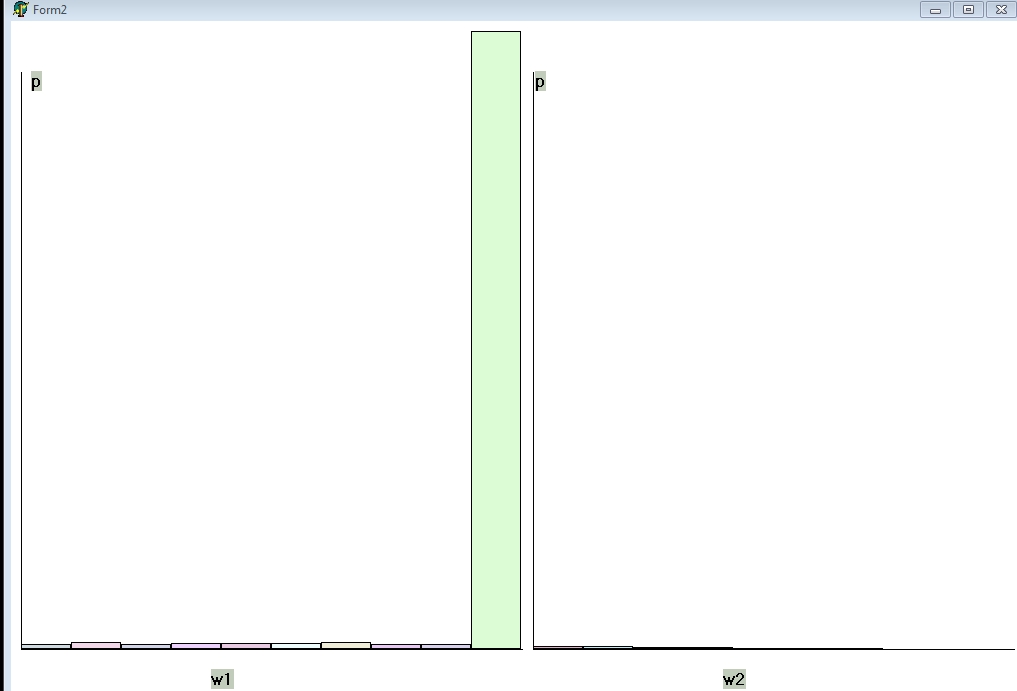
Рисунок 22. Кризис наступил, w₁=w₂=10

31