Заключение список литературы

[1] Бережная Е.В., Бережной В.И. Математические методы моделирования экономических систем: Учеб. пособие. – 2-е изд., перераб. и доп. – М.: Финансы и статистика, 2006.

[2] Бусленко Н. П. Моделирование сложных систем. – М.: Наука, 1988.

[3] Вентцель Е.С. Исследование операций. – М.: Советское радио, 1972 г.

[4] Вентцель Е.С. Задачи и упражнения по теории вероятностей: Учеб. пособие для студ.втузов/ Е.С. Вентцель, Л.А. Овчаров. – 5-е издание., испр. – М.: Издательский центр «Академия», 2003.

[5] Волков И.К., Загоруйко Е.А. Исследование операций: Учеб. для вузов/Под ред. В.С. Зарубина, А.П. Крищенко. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2000.

[6] Волковец А.И. Теория вероятностей и математическая статистика: Конспект лекций /А.И. Волковец, А.Б. Гуринович. – Мн.: БГУИР, 2003.

[7] Гмурман в.Е. 9-е изд., стер.—м.: Высшая школа, 2003.— 479 с. Книга (8 - е изд. - 2002 г.)

[8] Замятина Е.Б. Современные теории имитационного моделирования: Специальный курс. – Пермь: ПГУ, 2007.

[9] «Информатика и образование», журнал, выпуск №12. – М.: Образование и Информатика, 2003.

[10] Соболь И.М. «Метод Монте-Карло», Москва «Наука»,1985 г.

[11] Советов Б. Я., Яковлев С. А. Моделирование систем (3-е изд., перераб. и доп.). — М.: Высшая школа, 2001.

[12] Чернышов В.Н., Чернышов А.В. Теория систем и системный анализ: учебное пособие. – Тамбов: Изд-во Тамб. гос. техн. ун-та, 2008.

[13] Шеннон Р.N. Название: Имитационное моделирование систем - искусство и наука: Пер. с англ., 1978.

Приложение

Имеется магазин с одним продавцом, в который случайным образом входят покупатели. Если продавец свободен, он начинает обслуживать покупателя сразу, если покупателей несколько, выстраивается очередь. Смоделировать работу системы – означает вычислить, какое среднее время приходится стоять в очереди к продавцу, среднее время, проведенное продавцом в ожидании покупателя, и каково распределение этих величин.

Суть имитационного метода при изучении СМО состоит в том, что с помощью специальных устройств-датчиков случайных чисел вырабатываются интервалы между моментами последовательного поступления вызовов и все другие случайные величины, участвующие в процессе. Многократно имитируя течение процесса обслуживания, накапливается необходимый статистический материал, который используется для вычисления показателя качества.

Данная система представляет собой одноканальную систему массового обслуживания с ожиданием. На входе задачи – случайный процесс прихода покупателей в магазин, где промежутки между приходами любой последовательной пары покупателей – независимые случайные события, распределенные по некоторому закону. Реальный характер этого закона может быть установлен лишь путем многочисленных наблюдений; в качестве простейшей модельной функции плотности вероятности можно взять равновероятное распределение в диапазоне времени от 0 до некоторого – максимально возможного промежутка между приходами двух последовательных покупателей.

Такое распределение, конечно, мало реалистично; реально оно имеет максимум при некотором значении и быстро спадает при больших , т.е. имеет вид, изображенный на рисунке 18:

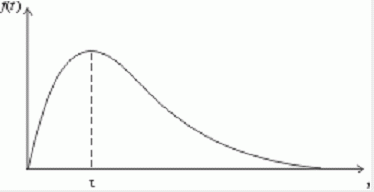
Рисунок 18. Типичная плотность вероятности распределения времени между приходами покупателей.

Т.е. промежутки времени между приходами имеют экспоненциальное распределение, следовательно, моменты поступления требований в систему распределены по закону Пуассона: где

– некоторая константа,

– произвольное целое. Функции имеют максимум при и нормированы:

Еще один случайный процесс в этой задаче сводится к последовательности случайных событий – длительностей обслуживания каждого из покупателей. Распределение вероятностей длительности обслуживания качественно имеет тот же вид, что и в предыдущем случае.

Нужно найти среднее время, которое приходится стоять в очереди – и среднее время, проведенное продавцом в ожидании покупателя Для этого с помощью элементарных расчетов найдем, сколько времени проводит в очереди один покупатель: где

– длительность времени, проведенного покупателем в магазине в целом;

– длительность обслуживания;

где

– момент конца обслуживания;

– момент начала обслуживания очередного покупателя определяется либо временем его прихода (если магазин пуст), либо временем ухода предыдущего покупателя;

– условное время прихода покупателя, где – промежутки между приходами покупателей (в минутах).

Составим таблицу 1, где в колонках и записаны случайные числа (для определенности взято и ), а остальные колонки заполняются с помощью соответствующих формул. Эта таблица дает возможность увидеть, каким образом, при данных случайных наборах чисел в колонках и покупателям приходится стоять в очереди (колонка ), и продавцу в ожидании покупателя (колонка ):

№ п/п
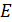
1	0	4	0	0	4	4	0	0
2	2	1	2	4	5	3	2	0
3	10	5	12	12	17	5	0	7
4	1	2	13	17	19	6	4	0
5	6	3	19	19	2	3	0	0

Таблица 1

Необходимо ответить на вопрос, каково распределение случайных величин и при заданных распределениях случайных величин и . Допустим, в простейшем моделировании мы примем гипотезу о равновероятных распределениях величин и – скажем, для в диапазоне от 0 до 10 минут и – от 0 до 5 минут. Для построения методом статистических испытаний распределения величин и поступим так: найдем в достаточно длинной серии испытаний (реально – в десятках тысяч, что на компьютере делается достаточно быстро) значения (для Н все делается аналогично) и разделим промежуток [0, ] на равных частей скажем, вначале на 10 – так, чтобы в каждую часть попало много значений . Разделив число попаданий в каждую из частей на общее число испытаний , получим набор чисел

Располагая функцией распределения, можно ответить на любой вопрос о характере процесса ожидания в очереди. Например, какова вероятность прождать дольше минут? Ответ будет получен, если найти отношение площади криволинейной трапеции, ограниченной графиком плотности распределения, прямой и , к площади всей фигуры.

Следующая программа позволяет моделировать описанный выше процесс. На выходе она дает средние значения и редние квадратические отклонения случайных величин и , полученные по выборке, максимальный объем которой порядка N:

unit Unit1; interface uses Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms, Dialogs, StdCtrls; type TForm1 = class(TForm) Button1: TButton; Memo1: TMemo; Memo2: TMemo; Button2: TButton; Button3: TButton; Label1: TLabel; Label2: TLabel; Button4: TButton; Edit1: TEdit; Edit2: TEdit; Label3: TLabel; Label4: TLabel; Label5: TLabel; Edit3: TEdit; procedure Button1Click(Sender: TObject); procedure Button2Click(Sender: TObject); procedure Button3Click(Sender: TObject); procedure Button4Click(Sender: TObject); private { Private declarations } public { Public declarations } end; var Form1: TForm1; a,b,c,d,e,f,Aa,Bb,Cc,Dd,Ee,Ff,Dg,Dh,max: real; s1,s2:double; i,k,j,i1,i2,w1,w2,N:integer; L1,L2,v:array[1..11] of real;

{L1-распределение g, L2-распределение h}

g,h:array[1..20000] of real; implementation uses Unit2; {$R *.dfm} procedure TForm1.Button1Click(Sender: TObject); begin randomize; w1:=strtoint(edit1.text);

{диапазон времен прихода от 0 до w1}

w2:=strtoint(edit2.text);

{диапазон времен обслуживания от 0 до w2}

N:=strtoint(edit3.text);

{число членов выборки}

Aa:=0; Bb:=w2*random; Cc:=0; Ee:=Bb; Ff:=bb;

{начальные значения}

g[1]:=0; h[1]:=0; for k:=1 to 11 do begin L1[k]:=0; L2[k]:=0; end; for i:=2 to n do begin a:=w1*random; b:=w2*random; c:=Cc+a; if c>Ee then d:=c else d:=Ee; e:=d+b; f:=e-c; g[i]:=f-b; h[i]:=d-Ee; Cc:=c; Ee:=e; if g[i]<=1 then L1[1]:=L1[1]+1; if h[i]<=0 then L2[1]:=L2[1]+1; for k:=2 to 10 do begin if (g[i]>k-1) and (g[i]<=k) then L1[k]:=L1[k]+1; if (h[i]>k-1) and (h[i]<=k) then L2[k]:=L2[k]+1; end; if g[i]>10 then L1[11]:=L1[11]+1; if h[i]>10 then L2[11]:=L2[11]+1; s1:=s1+g[i]; s2:=s2+h[i]; end;