21. При перемещении пробного заряда q в электрическом поле электрические силы совершают работу. Эта работа при малом перемещении равна :

Работа сил электростатического поля при перемещении заряда из одной точки поля в другую не зависит от формы траектории, а определяется только положением начальной и конечной точек и величиной заряда.

Следствием независимости работы от формы траектории является следующее утверждение: Работа сил электростатического поля при перемещении заряда по любой замкнутой траектории равна нулю.

Физическую величину, равную отношению потенциальной энергии электрического заряда в электростатическом поле к величине этого заряда, называют потенциалом φ электрического поля:

Потенциал φ является энергетической характеристикой электростатического поля.

Работа A₁₂ по перемещению электрического заряда q из начальной точки (1) в конечную точку (2) равна произведению заряда на разность потенциалов (φ₁ – φ₂) начальной и конечной точек: A₁₂ = W_p1 – W_p2 = qφ₁ – qφ₂ = q(φ₁ – φ₂).

В Международной системе единиц (СИ) единицей потенциала является вольт (В). 1 В = 1 Дж / 1 Кл.

22. Проводники

отличаются от диэлектриков наличием свободных носителей заряда. В металлических проводниках роль этих носителей выполняют свободные электроны, концентрация которых составляет приблизительно 10м–3 и они способны перемещаться под действием самой малой силы. Для того чтобы заряды оставались в равновесии необходимо выполнение следующих условий:

1.Напряженность электрического поля внутри проводника должна быть равной нулю:E0. Согласно формуле потенциал внутри проводника должен быть постонным  const

Воспользуйтесь электростатической теоремой Гаусса. Поток вектора напряженности электрического поля E через некоторую поверхность равен заряду, заключенному внутри этой поверхности. Если мы окружим проводящую сферу с зарядом сферой радиуса r, то поток вектора E через эту сферу будет равен: Ф = q/εε0 где ε0 - электрическая постоянная, ε - диэлектрическая проницаемость среды.

С другой стороны, т. к. вектор E будет перпендикулярен поверхности построенной нами сферы, то: Ф = E*S где S = 4πr² - площадьповерхности сферы. Тогда: E4πr² = q/εε0 или E(r) = (1/4πεε0r²)*q

В силу эквивалентности полей равномерно заряженной сферы и точечного заряда, напряженность поля в любой точке внешней области не изменится, если весь заряд сферы собрать в ее центре. Стало быть, не изменится и работаполя при движении пробного заряда по любой траектории во внешней области. А,значит,и выражение потенциальной

энергии

заряда

в поле заряда

также не изменится.

Таким образом потенциальная энергия взаимодействия пробного заряда, находящегося за пределами равномерно заряженной сферы и самой этой сферы определяется соотношением

Тогда, по определению потенциала,для внешней области

23. Электроемкость уединенного проводника - это физическая величина, численно равная заряду, необходимoму для повышения потенциала проводника на 1 В: Найдем емкость проводника формой шара радиуса R: 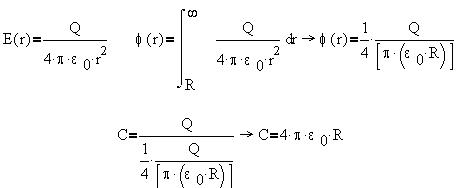Найдем размер шара емкостью 1Ф: При этом емкость шара размером в земной равна: Избыточный заряд величиной 1 Кл поднял бы потенциал такого шара на Как видим, емкость проводника определена его "габаритами". Совершенно аналогично, "энергетическая емкость" бочки, т. е. величина, численно равная массе воды, необходимой для повышения ее потенциала в поле тяжести на единицу (в однородном поле тяжести на высоте h потенциал численно равен потенциальной энергии 1 кг: gh), прямопропорциональна площади дна бочки. Диэлектрик в e раз ослабляет поле и, следовательно, в раз увеличивает емкость.

Электрический конденсатор представляет собой систему из двух проводников электрического тока (обкладок), разделенных диэлектриком. Основной характеристикой конденсатора является его электрическая емкость, или просто емкость, которая характеризует способность конденсатора накапливать электрический заряд.  Емкость конденсатора определяется отношением накапливаемого на одной из обкладок электрического заряда к приложенному напряжению: С=q/U. Она зависит от материала диэлектрика, формы и взаимного расположения обкладок.

В цепях постоянного тока конденсатор не проводит электрический ток, поскольку между его обкладками находится диэлектрик. В цепях переменного тока с конденсатором протекают токи его перезарядки. Емкостное сопротивление конденсатора обратно пропорционально частоте переменного тока и емкости, измеряется оно в омах.

Существуют конденсаторы постоянные (емкость которых нельзя изменить), полупеременные (подстроечные) и переменные. По роду диэлектрика выделяют бумажные, металлобумажные, пленочные, металлопленочные, слюдяные, керамические, стеклоэмалевые и воздушные конденсаторы.

- емкость конденсатора (С).

Если его пластины образуют параллельные плоскости, то его называют плоским.

- емкость плоского конденсатора. Зависит от площади его пластин S; от расстояния между его пластинами d; от материала, заполняющего пространство между пластинами ε. При изготовлении конденсатора большой емкости стремятся сделать большое S при малом d, а также заполнить его пространство веществами с большим ε. Не зависит от напряжения U и от заряда q. Формулы, где встречается С: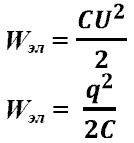 - энергия заряженного конденсатора

формула Т омсона для периода электромагнитных колебаний в колебательном контуре LC.