74.2. Плоскорадиальный фильтрационный поток упругой жидкости. Основная формула теории упругого режима фильтрации

Пусть в неограниченном горизонтальном пласте постоянной толщины И имеется добывающая скважина нулевого радиуса (точечный сток). Начальное пластовое давление во всем пласте одинаково и равно р_К. В момент времени t = 0 скважина пущена в эксплуатацию с постоянным объемным дебитом Q_o. В пласте образуется неустановившийся плоскорадиальный поток упругой жидкости. Распределение давления в пласте (в любой его точке в любой момент времени) p(r, t) определяется интегрированием уравнения пьезопроводности, которое для притока в цилиндрической системе координат имеет вид: (7.21)

Начальные и граничные условия:

р(r, t) = р_К при t = 0;

р(r,t) = p_к при r → ∞, t > 0;

при r = 0, t >0 . (7.22)

Первое условие означает, что до момента времени t = 0 во всем пласте давление было постоянным и равным контурному. Второе условие показывает, что граница возмущенной зоны (т.е. значение радиуса, на котором давление равно контурному) перемещается с ростом времени и для больших времен стремиться к бесконечности. Из третьего условия следует, что дебит скважины поддерживается постоянным. (вывод Басниев 2005 стр. 206, 1993 стр. 147)

Давление в любой точке плоскорадиального потока в условиях упругого режима фильтрации определяется

(7.23)

где - Ei – интегральная показательная функция (табулирована).

Формула (7.23) получила название основной формулы теории упругого режима фильтрации.

Если , то давление можно определять по формуле

(7.24)

Из (7.23) находят, что расход жидкости через любую цилиндрическую поверхность радиусом r и скорость фильтрации определяются

, (7.25)

И з последней формулы следует, что стационарная скорость достигается очень быстро на небольших расстояниях от скважины, т.к. значение коэффициента пьезопроводности обычно велико.

Пьезометрические кривые представляют собой логарифмические линии (рис. 5.4). Давление на забое скважины падает с течением времени, углы наклона касательных Θ на забое одинаковы для всех кривых.

Для геологов самостоятельно:

Интерференция скважин в условиях упругого режима (Басниев 2005 стр. 210, 1993 стр. 151) ,

Определение коллекторских свойств пласта по данным исследования скважин при упругом режиме (вывод Басниев 2005 стр. 215, 1993 стр. 156)

Приближенные методы решения задач теории упругого режима: метод последовательной смены стационарных состояний, метод А.М. Пирвердяна, метод интегральных соотношений, метод «усреднения» (вывод Басниев 2005 стр. 219, 1993 стр. 159)

Задачи в теме 8.

Тема 8. Неустановившееся движение газа в пористой среде

8.1. Дифференциальные уравнения неустановившейся фильтрации газа

Основы теории движения газа в пористой среде были разработаны основателем советской школы нефтегазовой гидромеханики академиком Л. С. Лейбензоном. Он впервые получил дифференциальные уравнения неустановившейся фильтрации совершенного газа в пласте по закону Дарси. Полученное им нелинейное дифференциальное уравнение параболического типа впоследствии было названо уравнением Лейбензона. При выводе указанного уравнения предполагалось, что коэффициенты пористости и проницаемости не изменяются с давлением, т.е. пласт недеформируем, вязкость газа также не зависит от давления, газ совершенный. Принимается также, что фильтрация газа в пласте происходит по изотермическому закону, т. е. температура газа и пласта остается неизменной по времени. Впоследствии один из учеников

Л. С. Лейбензона - Б. Б. Лапук в работах, посвященных теоретическим основам разработки месторождений природных газов, показал, что неустановившуюся фильтрацию газа можно приближенно рассматривать как изотермическую, так как изменения температуры газа, возникающие при изменении давления, в значительной мере компенсируются теплообменом со скелетом пористой среды, поверхность контакта газа с которой огромна. Однако при рассмотрении фильтрации газа в призабойной зоне неизотермичность процесса фильтрации сказывается существенно вследствие локализации основного перепада давления вблизи стенки скважины. На этом эффекте основано использование глубинных термограмм действующих скважин для уточнения профиля притока газа по толщине пласта (глубинная дебитометрия). При рассмотрении процесса фильтрации в пласте в целом этими локальными эффектами допустимо пренебрегать.

Дифференциальное уравнение неустановившейся изотермической фильтрации совершенного газа или уравнение Лейбензона

(8.1)

(8.1) представляет собой нелинейное дифференциальное уравнение в частных производных параболического типа, только одна неизвестная функция – давление. Уравнение справедливо только при выполнении закона Дарси.

Уравнение (8.1) можно после преобразований записать в декартовой системе координат

(8.2)

Уравнения (8.1), (8.2) представляют собой сложные нелинейные уравнения в частных производных, и в большинстве случаев не имеет точных аналитических решений.

Одним из способов решения уравнения Лейбензона является его линеаризация, т.е. сведение его к линейному уравнению Фурье. В результате оно упростится и решение будет приближенным.

Были предложены различные способы линеаризации уравнения (8.1). Если рассматривается плоскорадиальный приток к скважине, то, из теории установившейся фильтрации газа, воронка депрессии очень крутая, и в большей части пласта давление мало отличается от контурного. На этом основании Лейбензон предложил заменить переменное давление р в коэффициенте перед оператором Лапласа уравнения (8.1) на постоянное давление р_К, равное начальному давлению в пласте. Тогда, обозначив , получим вместо уравнения (8.1) уравнение

(8.3)

которое является линейным уравнением пьезопроводности относительно функции р², где η¯ - константа, аналогичная коэффициенту пьезопроводности. Такой способ линеаризации, когда переменный коэффициент в уравнении (8.3) при различных значениях давления принимается константой, называется линеаризацией по Лейбензону.

Используем линеаризованное уравнение (8.3) для решения конкретной задачи о притоке газа в скважину бесконечно малого радиуса (точечный сток), расположенную в пласте бесконечной протяженности с постоянной толщиной h. В начальный момент времени пласт невозмущен, т.е. давление во всем пласте постоянно и равно р_K. С этого момента начинается отбор газа с постоянным дебитом Q_am. Нужно найти изменение давления по пласту с течением времени р(r, t).

Для плоскорадиальной фильтрации газа (8.3) запишется следующим образом:

(8.4)

Интегрируем (8.4) при начальном условии p² (r, t) = p_K при t = 0 и граничном условии p² (r, t) = при t > 0, r →∞ . (8.5)

Условие для давления на забое скважины. Для этого запишем выражение массового дебита, исходя из закона Дарси в дифференциальной форме для плоскорадиальной фильтрации

Используя равенства , получим ^. Из последнего соотношения выразим условие на стенке газовой скважины бесконечного малого радиуса

при r = 0. (8.6)

Таким образом, для решения поставленной задачи уравнение (8.4) должно быть проинтегрировано при условиях (8.5, 6) и получаем основное решение линеаризованного уравнения Лейбензона для газа

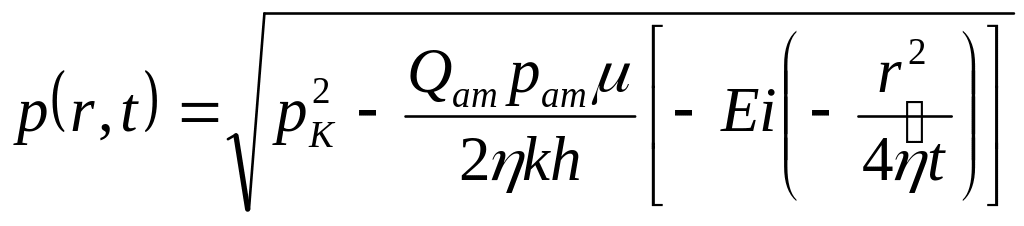или (8.7)

Для малых значений аргумента можно заменить интегральную показательную функцию на логарифмическую

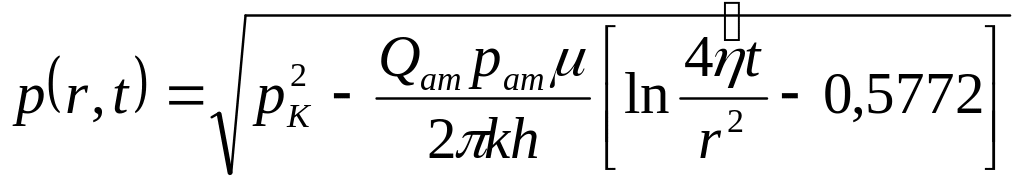(8.8)

Формулы (8.7) и (8.8) определяют (при фиксированных значениях времени t) распределение давления вокруг газовой скважины, работающей с постоянным дебит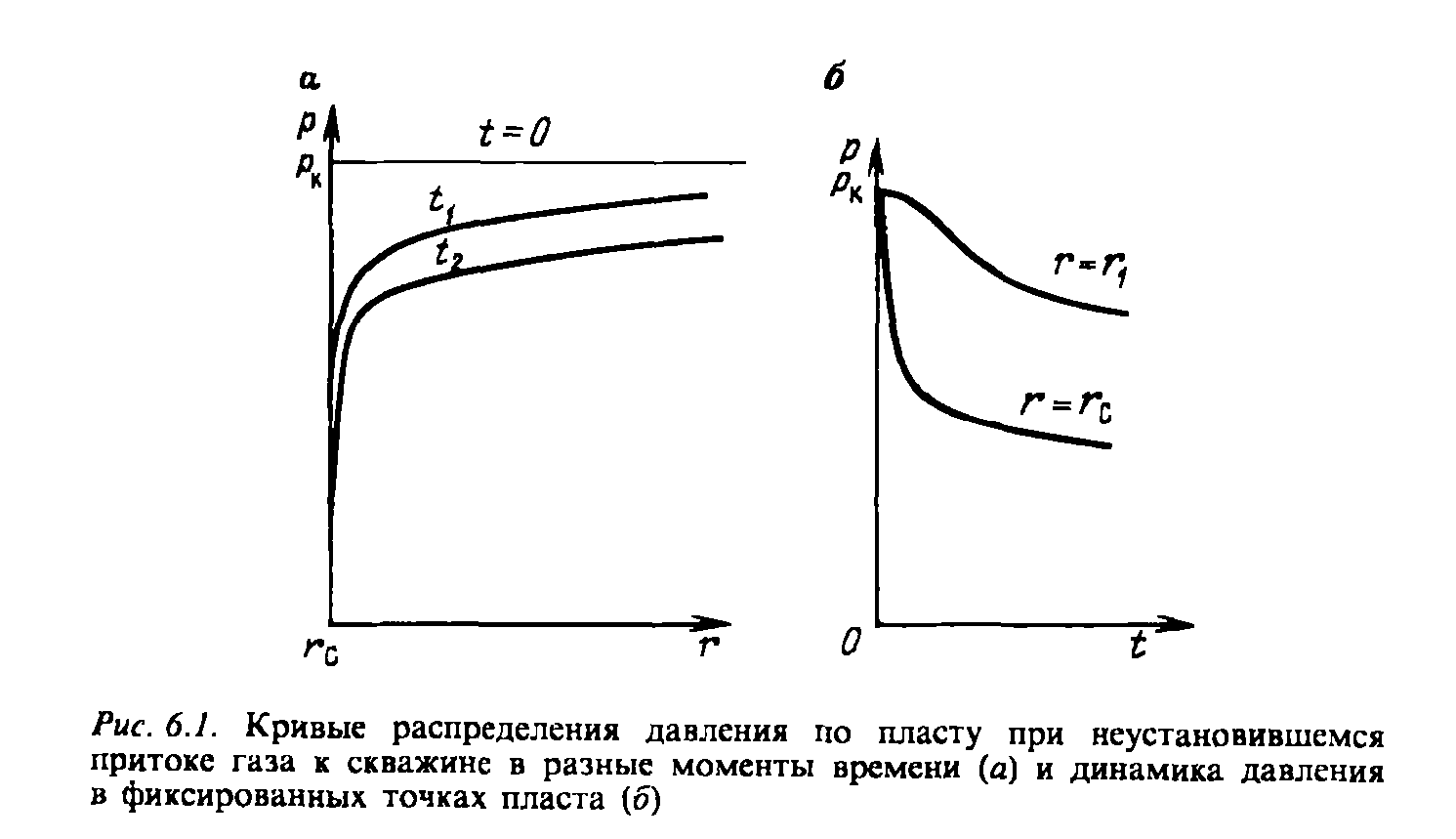 ом с момента t = 0. Эти депрессионные кривые имеют такой же характер, как при установившейся фильтрации – они очень крутые вблизи скважины (рис. 6.1,а). Если задать значение r, то можно найти изменение давления в данной точке с течением времени. В частности, можно найти изменение давления на забое (при r = r_с) после начала работы скважины (рис. 6.1,б):

Существуют и другие методы решения дифференциального уравнения Лейбензона: метод последовательной смены стационарных состояний, метод «усреднения» /Басниев, 2005 стр. 241/

Контрольные вопросы и задачи

1. Как записывается уравнение Лейбензона? Какого типа это уравнение?

2. Покажите, что для неустановившейся фильтрации газа принцип суперпозиции относительно давления не имеет места.

3. Как записывается дифференциальное уравнение неустановившейся, фильтрации газа, линеаризованное по Лейбензону?

4. Почему для плоскорадиальной фильтрации газа линеаризация дает очень маленькую погрешность при определении давления?

5. Какой вид имеет решение линеаризованного уравнения для плоскорадиального притока газа к скважине с постоянным дебитом?

6. Каковы предпосылки метода последовательной смены стационарных состояний? Как изменяется радиус возмущенной области с течением времени?

7. Как применяется принцип суперпозиции к задачам неустановившейся фильтрации газа?

8. Какие условия должны выполняться, чтобы при восстановлении давления в скважине зависимость от ln t' была линейной?

9. Какой вид имеет уравнение материального баланса для замкнутой газовой залежи (уравнение истощения газовой залежи)?

10. Каким будет закон изменения давления на границе замкнутой газовой залежи, если отбор происходит: а) при условии Q_am = const; б) при условии р_с = const?

124