7.2. Подсчет упругого запаса жидкости в пласте

Под упругим запасом жидкости в пласте понимается количество жидкости, которое можно извлечь из пласта при снижении давления в нем за счет объемной упругости пласта и насыщающих его жидкостей. Хотя коэффициенты объемной упругой деформации жидкости и пласта очень малы, зато очень велики объемы пласта.

Поэтому упругий запас жидкости в пласте может быть весьма существенным.

При снижении давления в пласте упругий запас жидкости естественно убывает, а при повышении давления происходит накопление упругого запаса жидкости в нем.

Упругий запас жидкости в пласте можно подсчитать следующим образом.

Выделим мысленно элемент объема пласта V_o. Пусть V_oж есть объем жидкости, насыщающей этот элемент объема пласта V_o при начальном давлении р₀. Упругий запас жидкости будем определять по ее объему, замеряемому при начальном пластовом давлении. Обозначим через ΔV_з изменение упругого запаса жидкости внутри объема пласта V_o при изменении давления во всех его точках на величину Δр. Тогда, можно записать ,

Изменение упругого запаса складывается

(7.1)

При определении формулы для коэффициента объемного сжатия жидкости β_ж считалось, что на жидкость действует только сжимающее гидростатическое давление, поэтому при увеличении давления (сжатия) объем жидкости уменьшается и наоборот, при уменьшении давления объем возрастает. Поэтому перед коэффициентом β_ж стоит знак «минус». В случае упругого режима при падении давления в пласте объем жидкости уменьшается. Это обусловлено тем, что жидкость рассматривается в порах, при уменьшении давления объем пор уменьшается и жидкость испытывает сжимающее действие со стороны твердого скелета. Поэтому знак «минус» перед β_с опускается.

Учитывая, что начальный объем жидкости, насыщающей элемент объема пласта V_o, равен полному объему пор в этом элементе:

, (7.2)

где m - пористость пласта.

Тогда формулу (7.1) с учетом равенства (7.2) можно представить в следующем виде:

(7.3)

Или (7.4)

где - коэффициент упругоемкости пласта или из (7.4) .

Для замкнуто-упругого режима под V₀ понимают объем пласта, к которому к данному моменту времени произошло изменение давления на величину Δр, при этом , (7.5)

где р_к – начальное пластовое давление, р¯- средневзвешенное по объему возмущенной части пласта V₀ давление.

С другой стороны, изменение упругого запаса жидкости в пласте за время dt равно объему отобранной из пласта нефти, тогда дифференциальное уравнение истощения нефтяной залежи в условиях замкнуто-упругого режима

(7.6)

где Q – дебит всех скважин, эксплуатирующих данную нефтяную залежь.

7.3. Дифференциальное уравнение фильтрации упругой жидкости в упругой пористой среде по закону Дарси

Полная система уравнений имеет вид

,

уравнение состояния упругой жидкости (вывод в теме 3) ,

уравнение состояния упругой пористой среды ,

k = const, μ = const , .

Все уравнения системы определяют математическую модель, но для постановки и решения задач необходимо преобразовать уравнения, чтобы получить одно дифференциальное уравнение для одной искомой функции. Для этого рассмотрим первое уравнение системы, подставив в него функцию Лейбензона

(7.7)

После подстановки формул пористости m и плотности ρ в левую часть (7.7) и дифференцирования по времени получим (7.8)

Подставляя под знак интеграла (7.7) уравнение состояния упругой жидкости и учитывая, что жидкость слабосжимаемая и коэффициент β_ж – мал, получим

(7.9)

Подставив (7.8) и (7.9) получим дифференциальное уравнение относительно давления:

(7.10)

или в декартовой системе координат (7.11)

где коэффициент \эта строчная\ , характеризующий скорость перераспределения давления при неустановившейся фильтрации упругой жидкости в упругой пористой среде или коэффициент пьезопроводности, лежит в пределах 0,1 – 5 м²/с.

Уравнение (7.10) – основное дифференциальное уравнение теории упругого режима фильтрации или по Щелкачеву В.Н. уравнение пьезопроводности.

Уравнение пьезопроводности (7.10) применимо только для слабосжимаемой упругой жидкости, для которой β_ж(р – р₀) < < 1. Если же это условие не выполняется, то пренебрегать под знаком интеграла в уравнении (7.9) коэффициентом β_ж нельзя. При этом дифференциальное уравнение значительно усложнится и примет нелинейный вид.

7.4. Одномерные фильтрационные потоки упругой жидкости.

Точные решения уравнения пьезопроводности.

Основная формула теории упругого режима

Рассмотрим наиболее простые точные решения уравнения пьезопроводности (7.10) для одномерных потоков.

7.4.1. Прямолинейно-параллельный фильтрационный поток упругой жидкости

Случай 1. Приток к галерее, на которой поддерживается постоянное давление.

Пусть в полубесконечном горизонтальном пласте постоянной толщины h и ширины В начальное пластовое давление всюду постоянно и равно р_K. На галерее (при х = 0) давление мгновенно снижено до р_Г и в дальнейшем поддерживается постоянным (т.е. p_Г = const). В удаленных точках (х → ∞) давление в любой момент времени остается равным р.

В пласте образуется неустановившийся прямолинейно-параллельный поток упругой жидкости. Давление в любой точке потока х и в любой момент времени t можно определить, интегрируя уравнение пьезопроводности (7.10), которое для одномерного течения в декартовой системе координат запишется

0 < х < ∞. (7.12)

Начальные и граничные условия, сформулированные выше и записанные виде математических соотношений, будут следующие:

р(х,t)= p_к при t = 0;

р(x,t)= p_r при x = 0, t >0;

р(x,t) = p_к при х = ∞, t ≥ 0. (7.13)

Задача заключается в определении дебита галереи Q(t) и давления в любой точке потока и в любой момент времени p(x,t).

Используя анализ размерностей, покажем, что поставленная задача автомодельна, т.е. из аргументов, от которых зависит давление, можно составить один безразмерный комплекс, от которого будет зависеть искомая функция p(x,t).

Обозначим через P = (p-p_r)/(p_к-р_r) безразмерное давление, которое, как следует из соотношений (7.12) и (7.13), зависит от времени t, координаты х и коэффициента пьезопроводности η, т.е.

P = f(x, t, η).

Размерности этих аргументов следующие: длина [x] = L, время [t] = T, [η] = L²T^-1, и из них можно составить безразмерный комплекс или переменную безразмерную величину . Задача сводится к нахождению безразмерного давления Р зависящего от u (автомодельной переменной): P = f(u) с граничными условиями

Р = 0 при u = 0; P = 1 при u = ∞. (7.14)

В силу линейности дифференциального уравнения (7.12) для безразмерного давления Р имеем такое же уравнение, как и для размерного р

(7.15)

Используя правило дифференцирования сложных функций, частные производные по координате и времени выражают через производные по безразмерной (автомодельной) производной, затем подставляют граничные условия (7.14) в (7.15), интегрируют и получают закон распределения давления в неустановившемся прямолинейно-параллельном фильтрационном потоке упругой жидкости (вывод Басниев 2005 стр. 199, 1993 стр. 140)

(7.16)

Т ипичные кривые распределения давления в различные моменты времени в неустановившемся прямолинейно-параллельном потоке упругой жидкости в галерее, пушенной в эксплуатацию с постоянным забойным давлением р_г = const, приведены на рис. 5.1.

Дебит галереи Q считаем положительным, отбираемый из галереи (х = 0), когда поток движется против оси х.

(7.17)

И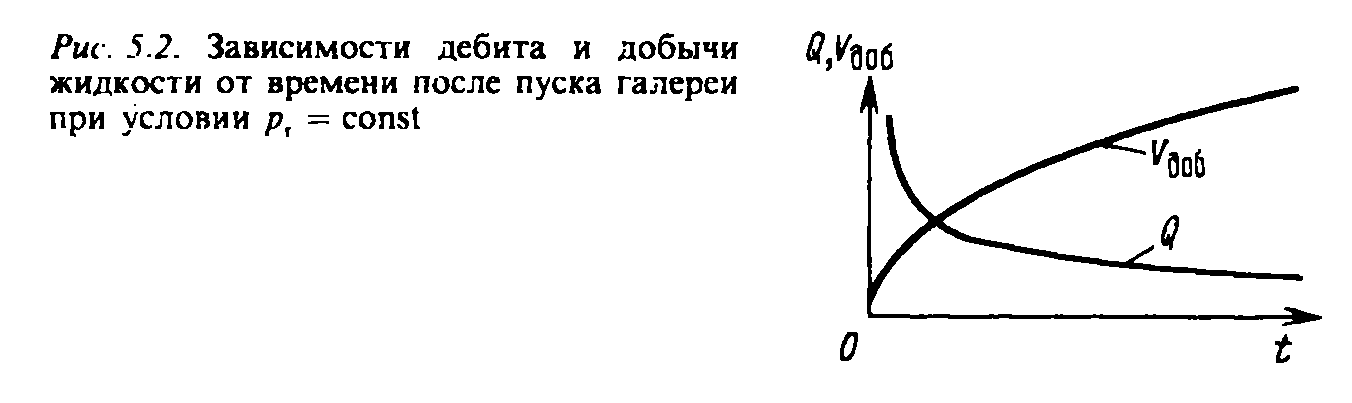 з формулы (7.17) следует, что дебит галереи убывает с течением времени как и при t → ∞ стремится к нулю. В начальный момент времени t = 0 формула (7.17) дает бесконечное значение дебита, что является следствием скачка давления на галерее (от р_К до р_г).

Накопленная к моменту t добыча V_доб (объем добытой нефти) определяется по формуле:

(7.18)

Т.е. сразу после начала отбора из галереи она быстро возрастает, а в дальнейшем растет очень медленно (рис. 5.2).

Случай 2. Приток к галерее, на которой поддерживается постоянный дебит.

В таком же полубесконечном пласте, что и в случае 1, в момент времени t = О пущена в эксплуатацию галерея с постоянным объемным дебитом Q. Требуется найти давление в любой точке пласта в любой момент времени. Математически задача заключается в интегрировании уравнения (7.15) при следующих начальных и граничных условиях:

р(х, t) = р_К при t = 0;

при x = 0, t >0;

р(x,t) = p_к при х → ∞, t > 0. (7.19)

Первое условие, как и в первом случае, задает распределение давления в пласте до пуска в галерее, и из него следует, что давление во всех точках пласта постоянно и равно контурному. Второе условие задает постоянство дебита на галерее после ее пуска. Из третьего условия следует, что граница возмущенной зоны с ростом времени перемещается к бесконечности. (вывод Басниев 2005 стр. 202, 1993 стр. 143)

(7.20)

Решение (7.20) при очень больших значениях теряет физический смысл. Полученный результат означает, что принятое граничное условие является слишком «жестким», для его реализации требуются отрицательные значения давления при большом времени. Реально эти давления возникать не будут - возникнет кавитация вблизи галереи.