Тема 6. Приток жидкости и газа к несовершенным скважинам. Учет несовершенства скважин.

6.1. Виды несовершенства скважин

Скважина называется гидродинамически совершенной, если она вскрывает продуктивный пласт на всю толщину и забой скважины открытый, т.е. вся вскрытая поверхность забоя является фильтрующей. Приток к такой скважине является плоскорадиальным.

Если скважина с открытым забоем вскрывает пласт не на всю толщину h, а только на некоторую глубину b, то ее называют гидродинамически несовершенной по степени вскрытия пласта. При этом называется относительным вскрытием пласта.

Если скважина вскрывает пласт до подошвы, но сообщение с пластом происходит только через специальные отверстия в обсадной колонне и цементном камне или через специальные фильтры, то такую скважину называют гидродинамически несовершенной по характеру вскрытия пласта.

Встречаются скважины и с двойным видом несовершенства – как по степени, так и по характеру вскрытия пласта. Степень вскрытия пласта имеет очень большое значение при разработке месторождений нефти и газа, так как они определяют фильтрационные сопротивления, возникающие в призабойной зоне, и, в конечном итоге, производительность скважин.

6.2. Приток жидкости к несовершенным скважинам при выполнении закона Дарси

Приток жидкости к несовершенной скважине даже в горизонтальном однородном пласте постоянной толщины перестает быть плоскорадиальным. Строгое математическое решение задачи о притоке жидкости к несовершенной скважине в пластах конечной толщины представляет большие трудности.

Путем подбора интенсивности расходов q и используя метод суперпозиции действительных и отображенных стоков, М. Маскет получил формулу для дебита гидродинамически несовершенной по степени вскрытия пласта скважины:

, (6.1)

где , (6.2)

функция степени вскрытия пласта - имеет следующее аналитическое выражение

, (6.3)

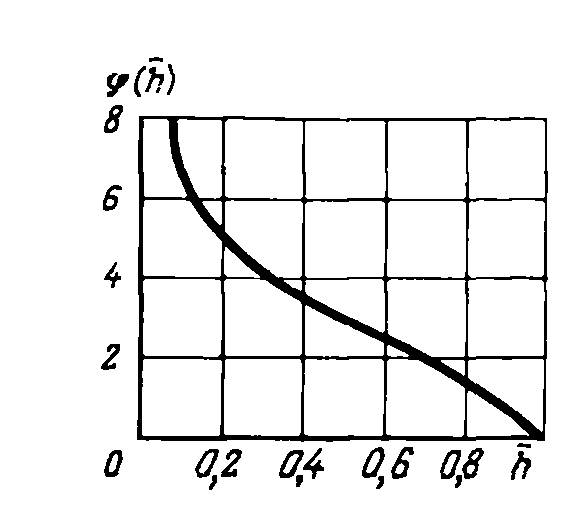г де - интеграл Эйлера второго рода, называется гамма – функцией, для которой имеются таблицы в математическом справочнике или графически (рис. 6.1, h заменить на δ).

При d = 1, т.е. пласт вскрыт полностью, (6.1) переходит в формулу Дюпюи для плоскорадиального потока.

Кроме того, для расчета несовершенной по степени вскрытия пласта скважины используется более простая формула, чем (6.1) М. Маскета, предложенная И. Козени:

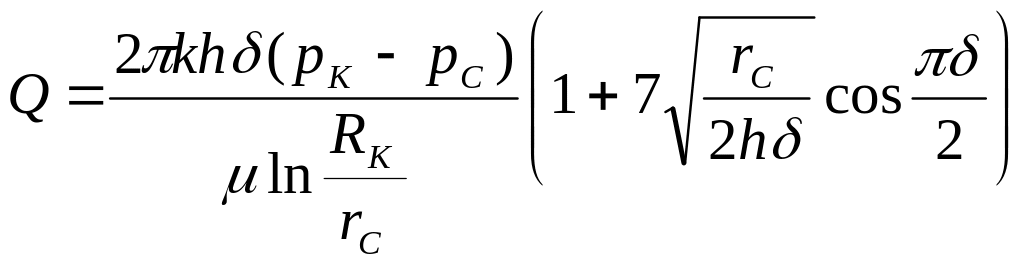(6.4)

Гидродинамическое несовершенство скважины характеризуется коэффициентом совершенства скважины

, (6.5)

где Q – дебит несовершенной скважины, Qсов – дебит совершенной скважины.

Широкое распространение получил метод расчета дебитов несовершенных скважин, основанный на электрогидродинамической аналогии фильтрационных процессов.

Дебит гидродинамически несовершенной скважины подсчитывается по формуле

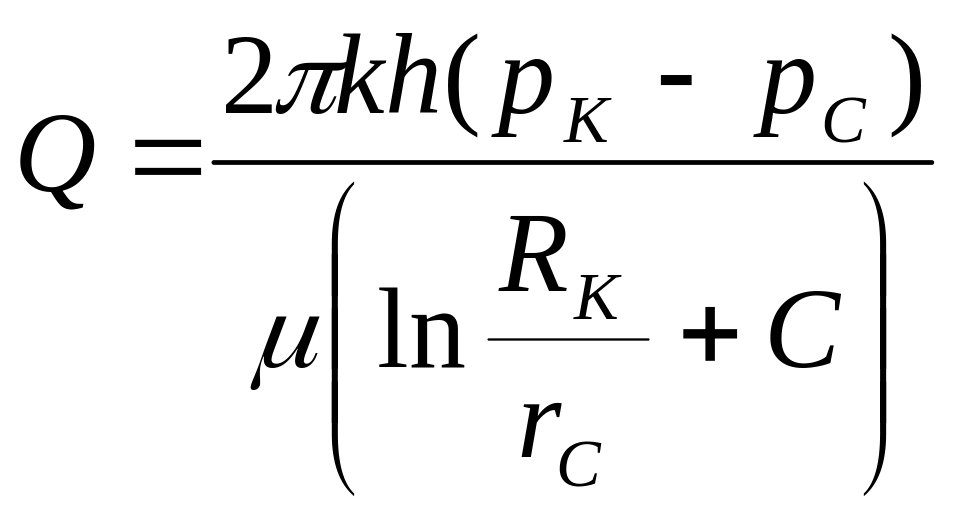, (6.6)

где С = С1 + С2 – дополнительное фильтрационное сопротивление, вызванное несовершенством скважины по степени вскрытия пласта (С1) и характеру вскрытия (С2).

Измеряя разность потенциалов и силу тока, можно подсчитать сопротивление по закону Ома, сделать пересчет на фильтрационное сопротивление и определить дополнительное фильтрационное сопротивление.

В.И. Щуровым были проведены такие экспериментальные исследования, в ходе которых им были определены дополнительные фильтрационные сопротивления С1 и С2 для различных видов несовершенства скважин и построены соответствующие графики /Басниев, 2005, стр. 175, 176/

Выражение дополнительного фильтрационного сопротивления получено И. А. Чарным с использованием формулы Маскета (6.1) в виде

, (6.7)

где j(d) определяется по формуле (239) или по графику.

А. М. Пирвердян получил для коэффициента С1 следующее выражение

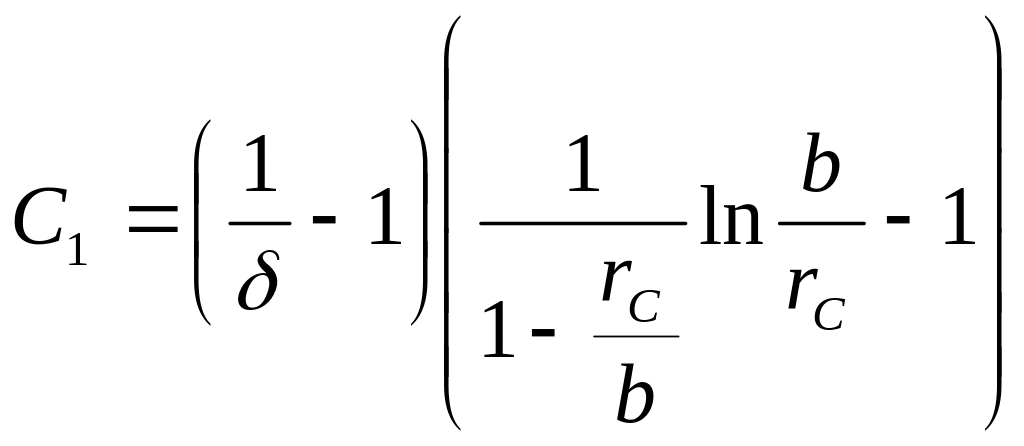(6.8)

Сравнив дебиты совершенной скважины (формула Дюпюи) и несовершенной скважины (6.6), получим выражение коэффициента совершенной скважины в следующем виде:

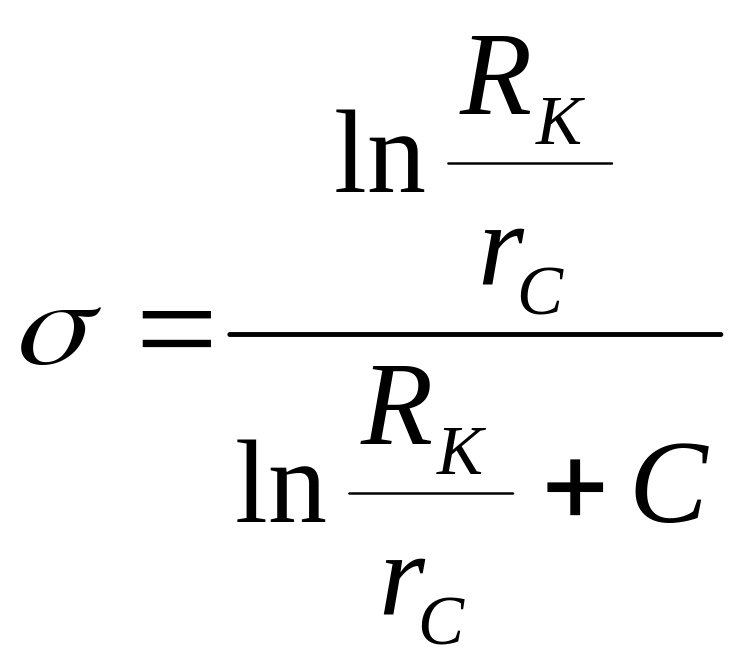. (6.9)

Иногда бывает удобно ввести понятие о приведенном радиусе скважин , т.е. радиусе такой совершенной скважины, дебит которой равен дебиту данной несовершенной скважины:

. (6.10)

Тогда (6.6) можно заменить следующей формулой:

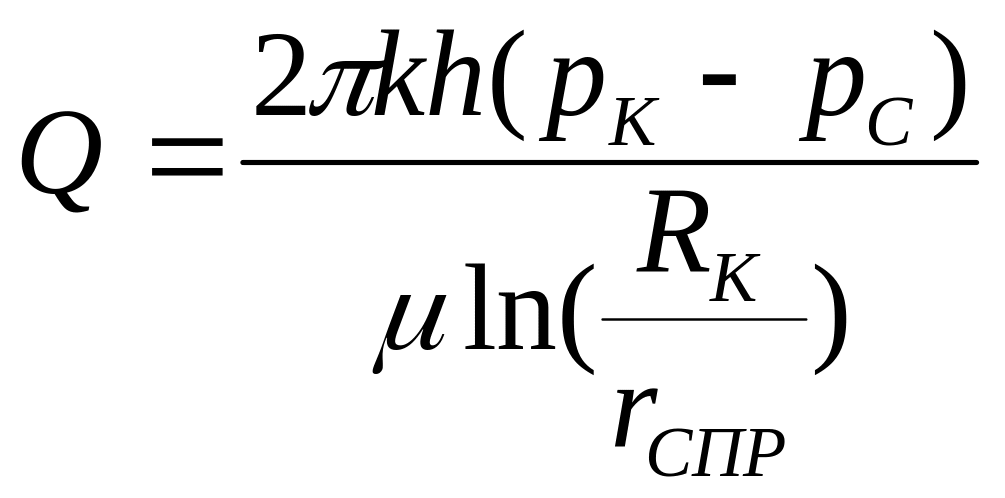. (6.11)

Самостоятельно

Приток газа к несовершенным скважинам при двучленном законе фильтрации, Басниев 2003 с.124

Приток несжимаемой жидкости к горизонтальной скважине, Басниев 2003 с. 126

Задачи.