
- •Тема 2. Математические модели однофазной фильтрации
- •2.1. Закон сохранения массы.
- •2.2. Закон сохранения количества движения (импульса) (вывод по н.Е. Жуковскому)
- •2.3. Замыкающие уравнения. Математические модели изотермической фильтрации
- •2.3.1. Модели однофазной фильтрации по закону Дарси в недеформируемом пласте
- •2.3.2. Вывод дифференциального уравнения неустановившейся фильтрации однородного флюида по закону Дарси. Функция л. С. Лейбензона.
- •2.3.2 Зависимость параметров флюидов и пористой среды от давления
- •2.3.3. Начальные и граничные условия
- •Тема 3. Одномерная установившаяся фильтрация несжимаемой жидкости и газа в пористой среде
- •3.1. Схемы одномерных фильтрационных потоков
- •3.2. Характеристики одномерных фильтрационных потоков жидкости и газов
- •Прямолинейно – параллельная фильтрация несжимаемой жидкости
- •П лоскорадиальная фильтрация несжимаемой жидкости
- •Радиально – сферическая фильтрация несжимаемой жидкости
- •3.3. Анализ одномерных потоков несжимаемой жидкости и газа
- •Прямолинейно – параллельный поток несжимаемой жидкости и совершенного газа
- •Плоскорадиальный фильтрационный поток
- •Радиально – сферический фильтрационный поток несжимаемой жидкости и совершенного газа
- •3.4. Фильтрационное плоскорадиальное течение реального газа по закону Дарси
- •3.5. Плоскорадиальный фильтрационный поток несжимаемой жидкости и газа по двучленному закону фильтрации
- •3.6. Плоскорадиальный фильтрационный поток несжимаемой жидкости и газа по степенному закону фильтрации
- •3.7. Одномерные фильтрационные потоки несжимаемой жидкости и газа в неоднородных пластах по закону Дарси
- •3.7.1. Прямолинейно – параллельный поток в неоднородных пластах
- •3 .7.2. Плоскорадиальный поток в неоднородных пластах
П лоскорадиальная фильтрация несжимаемой жидкости
Схема плоскорадиального потока в круговом пласте.
Пусть имеем в круговом пласте толщиной h и радиуса Rк центральную скважину радиуса rc, на забое которой поддерживается постоянное давление. На боковой поверхности r = Rк также поддерживается постоянное давление рк (рк > pс) и через нее происходит приток флюида, равный дебиту скважины. Поэтому фильтрация установившаяся, а боковая поверхность, через которую происходит приток, называется контуром питания.
От
координаты S переходим
к r, отсчитываемой от
центра скважины. Для добывающей скважины
![]() ,
,
![]() ,
площадь фильтрационной поверхности
,
площадь фильтрационной поверхности
![]() -
боковая поверхность цилиндра; на контуре
питания r1
= Rk
, р2 = рK на
забое скважины r2
= rc
, р2 = рC .
-
боковая поверхность цилиндра; на контуре
питания r1
= Rk
, р2 = рK на
забое скважины r2
= rc
, р2 = рC .
Выражение для дебита (объемного расхода) скважины
 (3.9)
(3.9)
Равенство (3.9) называется формулой Дюпюи, по имени французского инженера-гидравлика XIX века.
Формулы для распределения давления в пласте
![]() ,
,
![]() (3.10)
(3.10)
Или используя формулу Дюпюи равенства (3.10) можно привести к виду
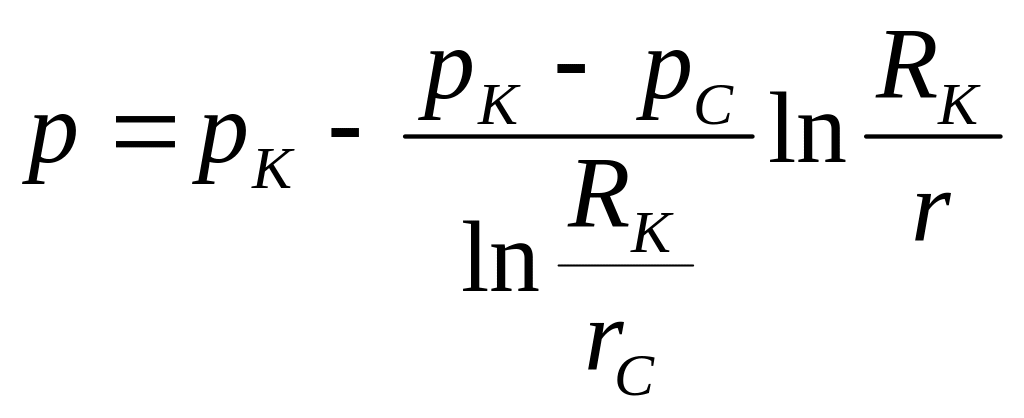 ,
,
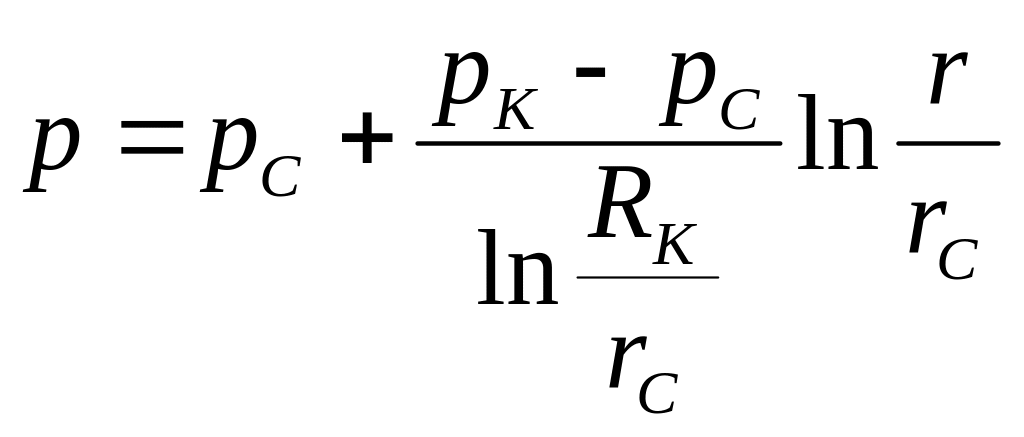 (3.11)
(3.11)
Ф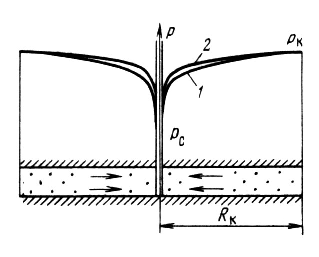 ормулы
(3.10, 3.11) эквивалентны, из них следует,
что давление в пласте распределено по
логарифмическому закону. Поэтому при
значениях радиуса, близких к контуру
питания, значения давления изменяются
не значительно, но при приближении к
скважине давление резко изменяется
(рис. 3.5, на рис.
кривые распределения в плоскорадиальном
потоке: 1 – для жидкости , 2 – для газа).
Формулы (3.10, 3.11) в пространстве и
определяют поверхности, которые
получаются вращением образующей вокруг
оси симметрии скважины. Поверхность,
соответствующая распределению давления,
носит название воронки депрессии.
Аналогично ведет себя и градиент давления
и скорость фильтрации (с той лишь
разницей, что давление при приближении
к скважине резко уменьшается, а скорость
возрастает).
ормулы
(3.10, 3.11) эквивалентны, из них следует,
что давление в пласте распределено по
логарифмическому закону. Поэтому при
значениях радиуса, близких к контуру
питания, значения давления изменяются
не значительно, но при приближении к
скважине давление резко изменяется
(рис. 3.5, на рис.
кривые распределения в плоскорадиальном
потоке: 1 – для жидкости , 2 – для газа).
Формулы (3.10, 3.11) в пространстве и
определяют поверхности, которые
получаются вращением образующей вокруг
оси симметрии скважины. Поверхность,
соответствующая распределению давления,
носит название воронки депрессии.
Аналогично ведет себя и градиент давления
и скорость фильтрации (с той лишь
разницей, что давление при приближении
к скважине резко уменьшается, а скорость
возрастает).
Проанализируем полученные соотношения для плоскорадиальной фильтрации. Для несжимаемой жидкости давление меняется вдоль координаты r по логарифмическому закону (рис. 3.8, кривая 1). Вращение кривой р (r) в пространстве вокруг оси скважины образует поверхность, называемую воронкой депрессии. В точке r = Rk - на контуре питания - кривая не касается горизонтальной линии, а пересекает ее под некоторым углом. Воронка депрессии вследствие логарифмического закона распределения давления имеет большую кривизну вблизи скважины. Следовательно, основная часть депрессии на пласт (рk - рс) сосредоточена в призабойной зоне скважины, параметры которой сильно влияют на дебит скважины. Давление одинаково в тех точках пласта, в которых r = const или, в декартовых координатах х 2 + у 2 = r 2 = const. Это означает, что изобарами (линиями равного давления) являются окружности, концентричные оси скважины. Траектории частиц - радиальные прямые - вместе с изобарами образуют фильтрационное поле течения к скважине. Семейства линий тока (траекторий) и изобар всегда ортогональны друг другу. Сравнение кривых распределения давления в круговом пласте для несжимаемой жидкости и газа при одинаковых граничных условиях показывает, что в газовом потоке имеет место более резкое падение давления вблизи скважины и весьма малое вдали от нее, так что кривая р (r) для газа располагается выше, чем для жидкости (см. рис. 3.8, кривая 2).
Скорость фильтрации определяется
![]() (3.12)
(3.12)
 Через
любую цилиндрическую поверхность,
концентрично расположенную относительно
скважины, в единицу времени протекает
один и тот же объем несжимаемой жидкости
(Q = const).
Поэтому вблизи контура питания площадь
боковой поверхности цилиндра очень
велика и скорости малы. При приближении
скважине площадь поверхности постоянно
уменьшается, и скорость возрастает
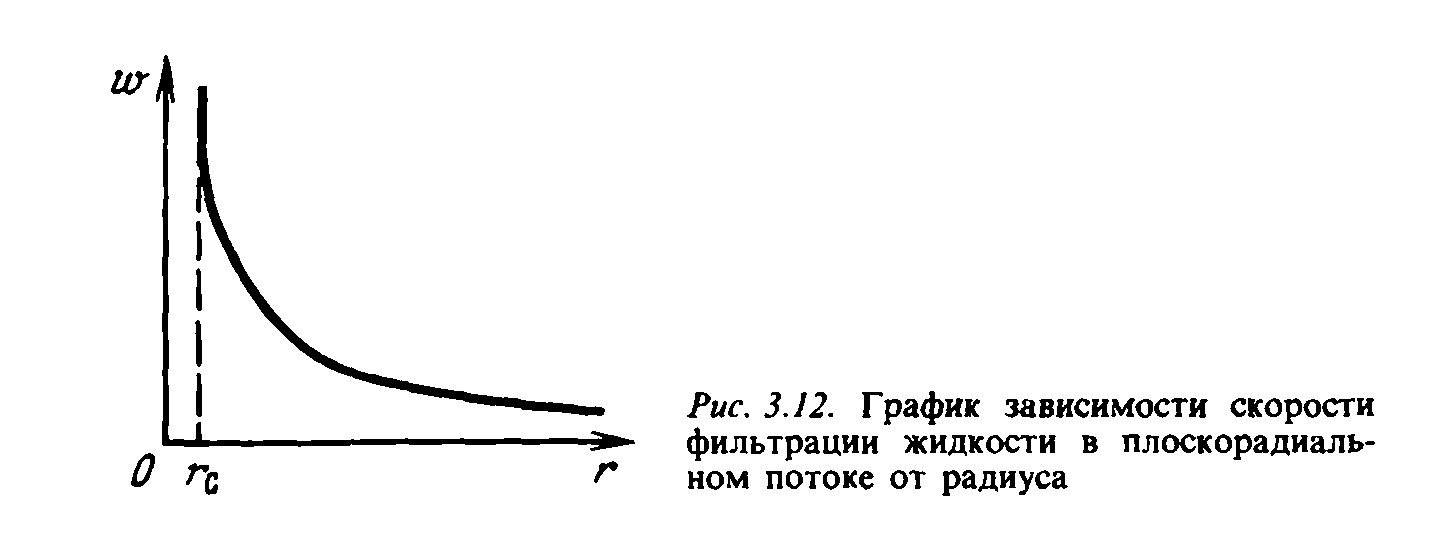
(рис. 3.6). Для того чтобы скорость
возрастала, необходимо увеличить
градиент давления.
Через
любую цилиндрическую поверхность,
концентрично расположенную относительно
скважины, в единицу времени протекает
один и тот же объем несжимаемой жидкости
(Q = const).
Поэтому вблизи контура питания площадь
боковой поверхности цилиндра очень
велика и скорости малы. При приближении
скважине площадь поверхности постоянно
уменьшается, и скорость возрастает
(рис. 3.6). Для того чтобы скорость
возрастала, необходимо увеличить
градиент давления.
У равнение
индикаторной линии при плоскорадиальном
потоке, также как и в случае фильтрации
в галерее, задается уравнением прямой
(рис. 3.7)
равнение
индикаторной линии при плоскорадиальном
потоке, также как и в случае фильтрации
в галерее, задается уравнением прямой
(рис. 3.7)
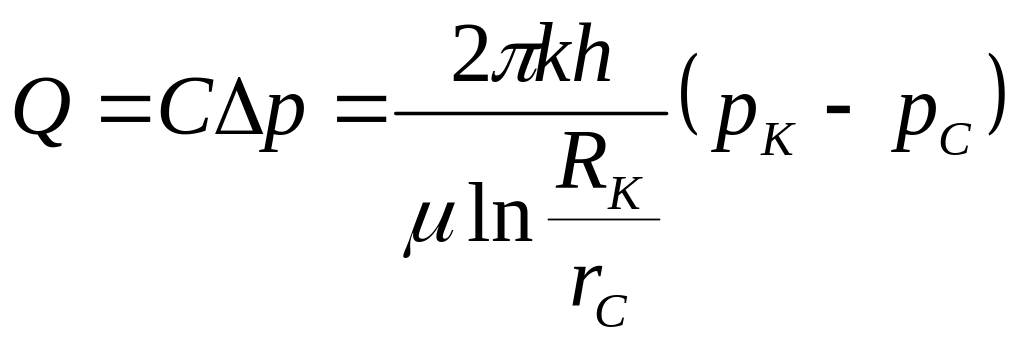 (3.13)
(3.13)
с коэффициентом продуктивности
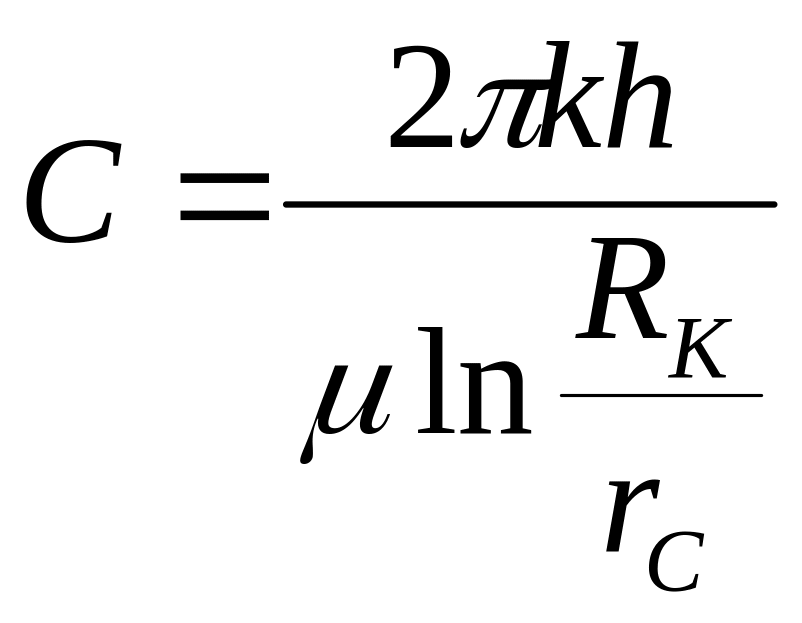 .
.
Вид индикаторной линии не зависит от геометрии потока и определяется только законом фильтрации. Отношение массового дебита скважины Qm к перепаду давления р называется коэффициентом продуктивности скважины С.
Из (3.13) для жидкости
![]() или
или
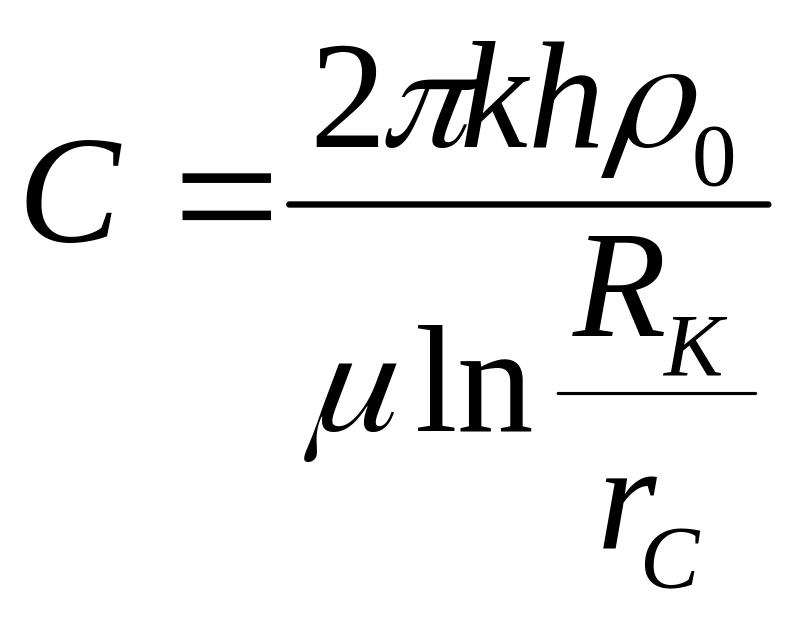
Коэффициент продуктивности определяется
в результате исследования скважины при
установившихся отборах. Если исследования
скважины выполнены при
![]() (
(![]() -
давление насыщения нефти газом), то по
тангенсу угла наклона коэффициент
продуктивности скважины
-
давление насыщения нефти газом), то по
тангенсу угла наклона коэффициент
продуктивности скважины
![]() ,
,
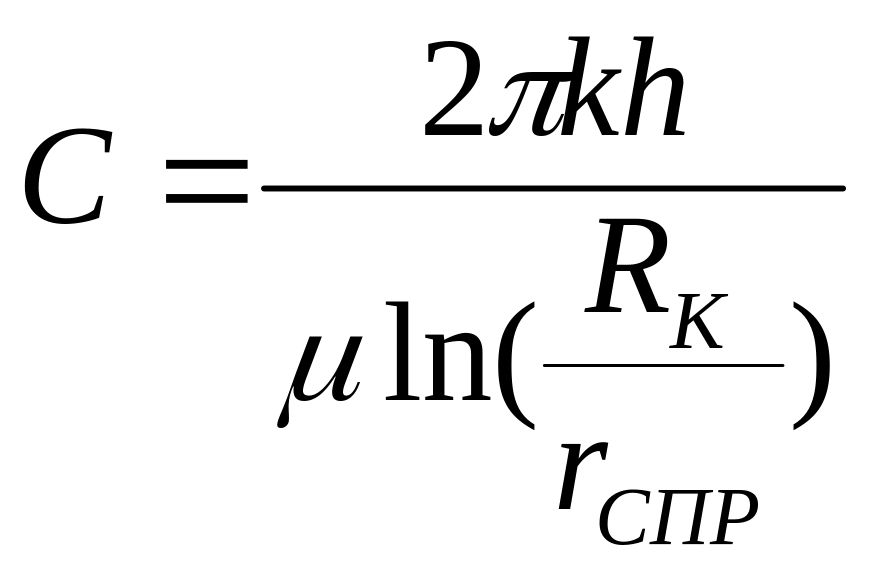 ,
,
где
![]() - приведенный радиус скважины.
- приведенный радиус скважины.
Приведенный радиус скважины – это
радиус гидродинамически совершенной
скважины, которая обеспечивает при
равных прочих условиях такой же дебит,
как гидродинамически несовершенная
скважина,
![]() .
.
Расчетные соотношения для определения времени движения «меченой частицы» в плоскорадиальном потоке.
Если пористость равна просветности время движения «меченой частицы» от контура питания до произвольной точки пласта
![]() или используя формулу Дюпюи
или используя формулу Дюпюи
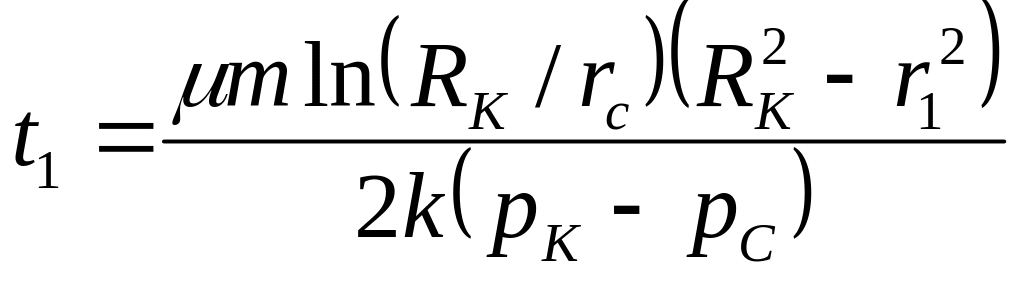 (3.14)
(3.14)
Из (3.14) следует, что «меченая частица» пройдет расстояние от контура питания до скважины за время Т
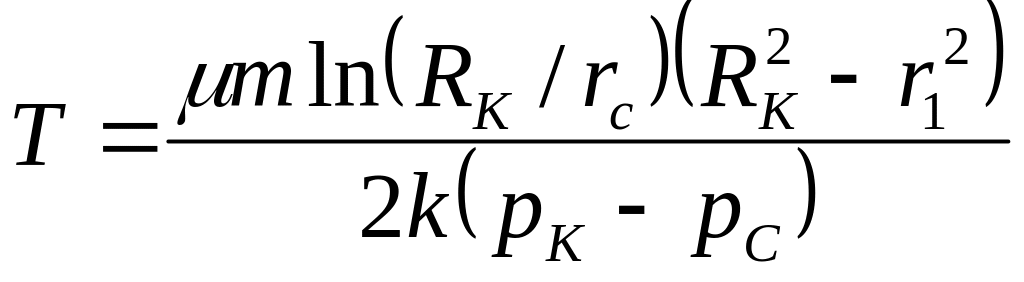 или rC/RK
<<1 то
или rC/RK
<<1 то
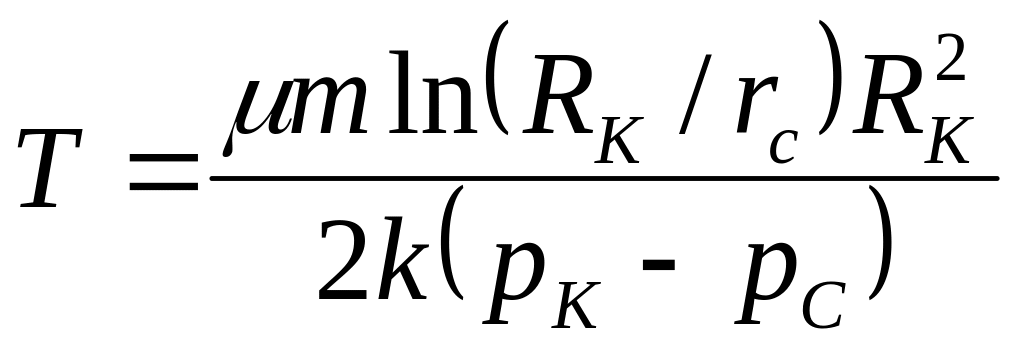 (3.15)
(3.15)
Если пористость неравна просветности, то появляется структурный коэффициент
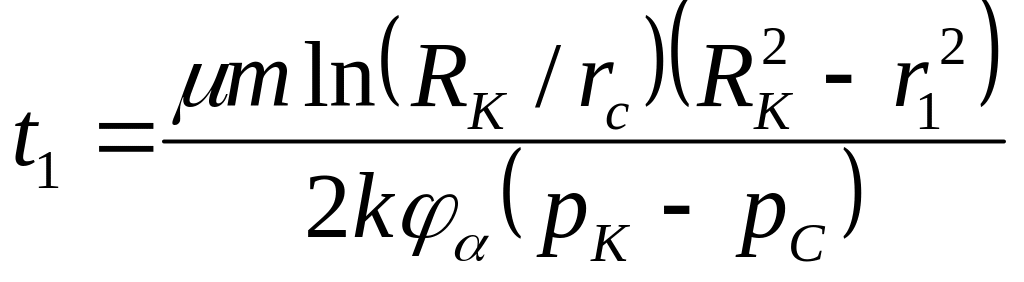 ,
,
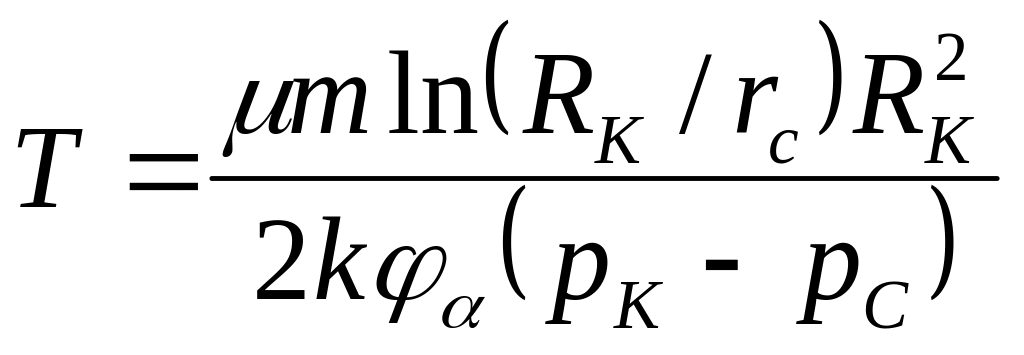 (3.16)
(3.16)
Средневзвешенное по поровому пространству давление при RK/rC >> 1
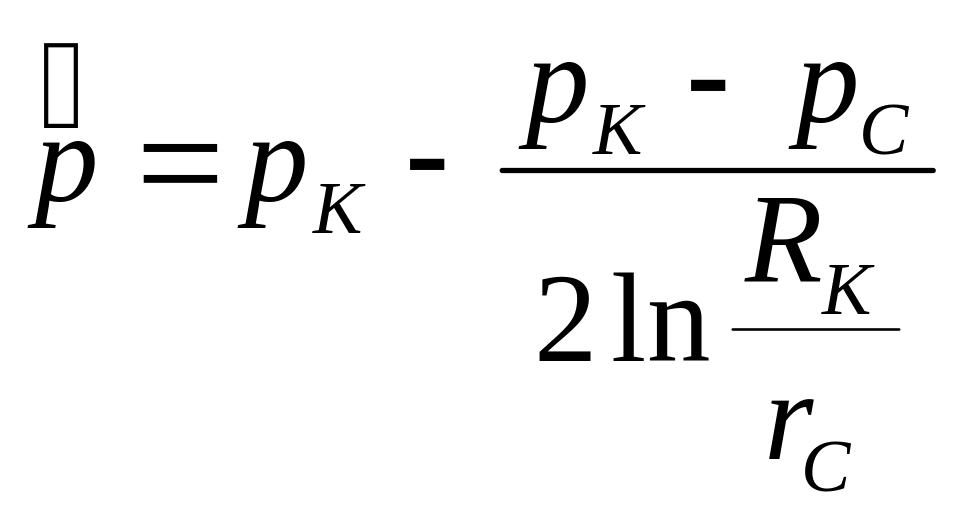 (3.17)
(3.17)
