Тема 3. Одномерная установившаяся фильтрация несжимаемой жидкости и газа в пористой среде

3.1. Схемы одномерных фильтрационных потоков

Одномерным называется фильтрационный поток жидкости или газа, в котором скорость фильтрации, давление и другие характеристики течения являются функциями только одной координаты, отсчитываемой вдоль линии тока. Одномерные фильтрационные потоки обладают различной симметрией. Различают:

1. Прямолинейно-параллельный поток. Траектории всех частиц жидкости - параллельные прямые, а скорости фильтрации во всех точках любого поперечного (перпендикулярного к линиям тока) сечения потока равны между собой, поверхности равных потенциалов (эквипотенциальные поверхности) и поверхности равных скоростей (изотахи) являются плоскими поверхностями перпендикулярными траекториям. Законы движения вдоль всех траекторий такого фильтрационного потока идентичны, а потому достаточно изучить движение вдоль одной из траекторий, которую можно принять за ось координат - ось х.

Примеры.

а) в лабораторных условиях при течении через цилиндрический керн или прямую трубу постоянного сечения, заполненную пористой средой.

б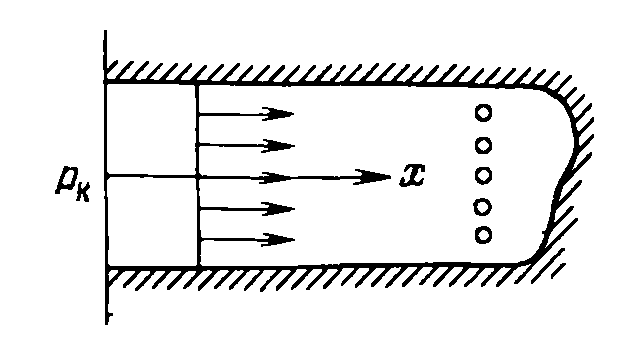 ) на отдельных участках продуктивного пласта при движении жидкости к батарее скважин, если пласт постоянной толщины имеет в плане форму прямоугольника (см. рис.). Линии тока будут искривляться только вблизи скважин. Если уплотнить сетку скважин в батарее заменить батарею сплошной прямолинейной выработкой галереей, то движение к галерее будет строго прямолинейно-параллельным. Поток можно считать прямолинейно-параллельным на некотором участке между нагнетательной и добывающей батареями скважин.

в) Поток между круговыми батареями нагнетательных и эксплуатационных скважин в случае больших радиусов батарей (угол схождения векторов скорости бесконечно мал). При этом толщина пласта постоянна, а его кровля и подошва непроницаемы.

П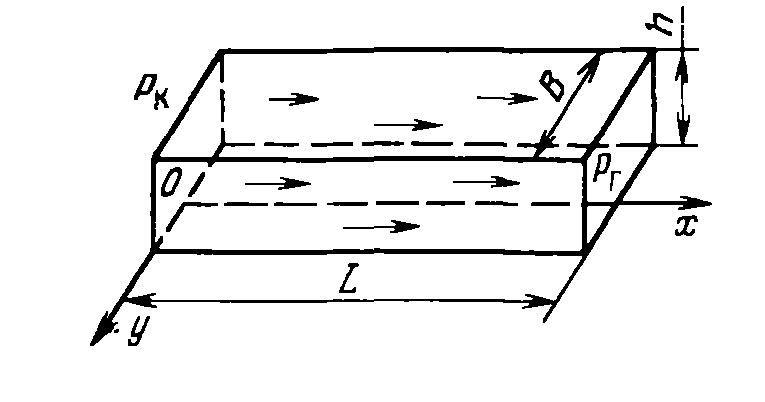 ласт, в котором имеет место прямолинейно-параллельный поток, удобно схематизировать в виде прямоугольного параллелепипеда высотой h (толщина пласта), шириной В и длиной L (рис. 3.2). Левая грань является контуром питания, здесь давление постоянно и равно р_к , правая грань - поверхность стока (галерея) с давлением р_г . Все остальные грани непроницаемы.

2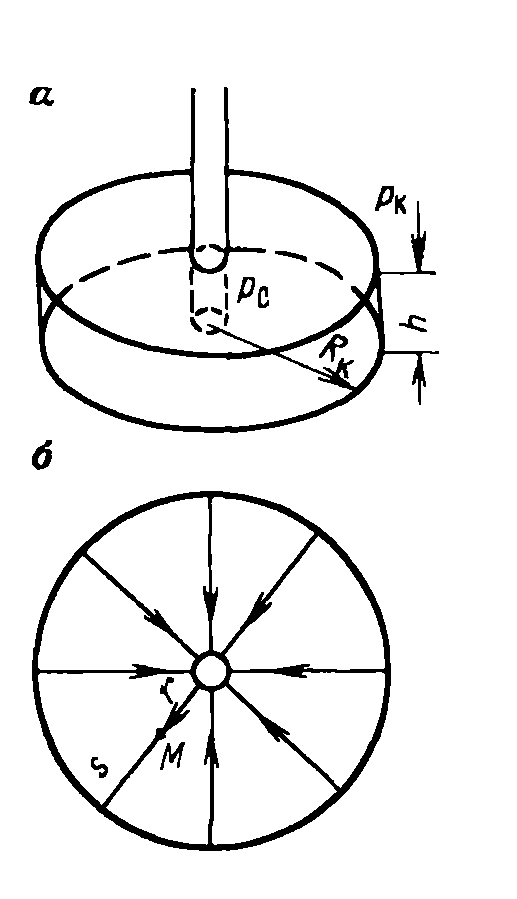 . Плоскорадиальный поток. Траектории всех частиц жидкости - прямолинейные горизонтальные прямые, радиально сходящиеся к центру скважины, а скорости фильтрации во всех точках любого поперечного (перпендикулярного к линиям тока) сечения потока параллельны и равны между собой; изотахи и эквипотенциальные поверхности перпендикулярны траекториям и образуют цилиндрические окружности с осью, совпадающей с осью скважины. Схемы линий тока в любой горизонтальной плоскости потока будут идентичными и для характеристики потока достаточно рассмотреть движение жидкости в одной горизонтальной плоскости.

Предположим, что имеется горизонтальный пласт постоянной толщины h и неограниченной или ограниченной протяженности. В пласте пробурена одна скважина, вскрывшая его на всю толщину и имеющая открытый забой.

При отборе жидкости или газа их частицы будут двигаться по горизонтальным траекториям, радиально сходящимся к скважине. Картина линий тока в любой горизонтальной плоскости будет одинакова, и для полной характеристики потока достаточно изучить движение флюида в одной горизонтальной плоскости. В плоскорадиальном одномерном потоке давление и скорость фильтрации в любой точке зависят только от расстояния r данной точки от оси скважины. На рис. 3.3, а, б приведена схема плоскорадиального фильтрационного потока. Схематизируемый пласт ограничен цилиндрической поверхностью радиусом R_k, (контуром питания), на которой давление постоянно и равно р_к; на цилиндрической поверхности скважины радиусом r_с (забой скважины) давление равно р_с. Кровля и подошва пласта непроницаемы. На рис. 3.3,б приведены сечение пласта горизонтальной плоскостью и радиальные линии тока, направленные к скважине. Если скважина не добывающая, а нагнетательная, то направление линий тока надо изменить на противоположное.

Примеры.

а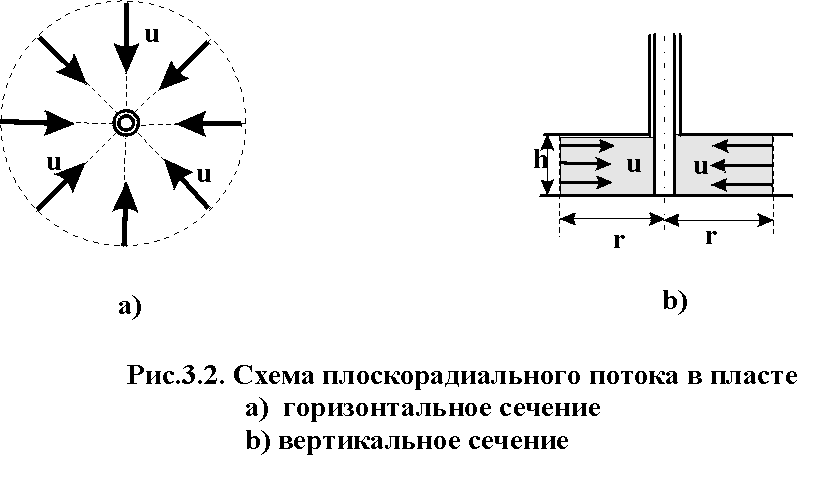 ) Горизонтальный пласт постоянной толщины (h) и неограниченной протяженности, подошва и кровля пласта непроницаемы. Пласт вскрыт единственной гидродинамически совершенной скважиной (рис. 3.2), т.е. вскрыт на всю толщину и забой полностью открыт. Для эксплуатационной скважины поток - радиально-сходящий, а для нагнетательной - радиально-расходящий. Плоско-радиальным потоком будет занята вся зона от стенки скважины до контура питания.

б) Гидродинамически - несовершенная скважина - вблизи скважины линии тока искривляются и поток можно считать плоско-радиальным только при некотором удалении от скважины.

в) Круговая батарея эксплуатационных скважин - поток плоско-радиален на некотором удалении, т.к. жидкость движется к укрупнённой скважине радиуса, равного радиусу окружности батареи.

г) Приток флюида в центральной скважине в круговом пласте.

3. Радиально-сферический поток. Траектории всех частиц жидкости - прямолинейные горизонтальные прямые, радиально сходящиеся к центру полусферического забоя; изотахи и эквипотенциальные поверхности перпендикулярны траекториям и образуют сферические поверхности. Скорость фильтрации в любой точке потока является функцией только расстояния этой точки от центра забоя. Следовательно, этот вид фильтрационного потока также является одномерным.

Р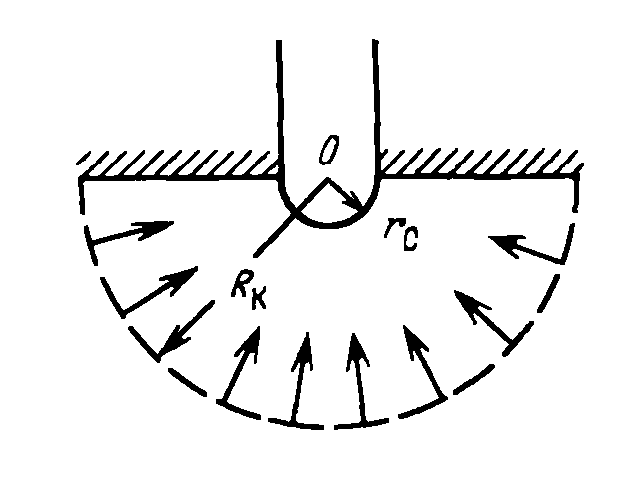 ассмотрим схему пласта неограниченной толщины с плоской горизонтальной непроницаемой кровлей. Скважина сообщается с пластом, имеющим форму полусферы радиусом R_k, (рис. 3.4). При эксплуатации такой скважины траектории движения всех частиц жидкости или газа в пласте будут прямолинейными в пространстве и радиально сходящимися в центре полусферического забоя, в точке О. В таком установившемся потоке давление и скорость в любой его точке будут функцией только расстояния r этой точки от центра полусферы.

Такой поток может реализовываться вблизи забоя, когда скважина вскрывает только самую кровлю пласта или глубина вскрытия h значительно меньше толщины пласта.

Описанные три вида одномерного потока играют большую роль при решении многих задач нефте-газопромысловой практики. Они лежат в основе ряда исследований закономерностей течения жидкости в пласте в зависимости от принятой системы разработки или от конструктивных особенностей скважин. Естественно, моделируя каждый из трёх видов одномерного потока, используют некоторую схематизацию реальных пластов и течений жидкости. Тем не менее, рассмотренные схемы не только воспроизводят хотя и приближенно простейшие случаи течения жидкости в реальном пласте, но и помогают изучать более сложные виды потоков пластовой жидкости в тех случаях, в которых сложный фильтрационный поток удобно представить себе состоящим из простейших видов потока.

К числу сложных потоков можно отнести: плоский фильтрационный поток в случае, когда число скважин не менее двух; многофазные течения и т.д.

Задача исследования установившегося фильтрационного потока заключается в определении дебита (расхода), давления, градиента давления и скорости фильтрации в любой точке потока, а также в установлении закона движения частиц жидкости (или газа) вдоль их траекторий и в определении средневзвешенного по объёму порового пространства пластового давления.

При условии вытеснения флюида из пласта или его нагнетания в пласт через галерею или скважину условимся принимать за координату произвольной точки пласта расстояние r до этой точки от:

1. галереи (для прямолинейно- параллельного потока);

2. центра контура скважины в основной плоскости (плоскости подошвы пласта) фильтрации (для плоско-радиального потока);

3. центра полусферического забоя скважины (для сферически-радиального потока).